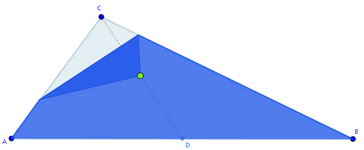
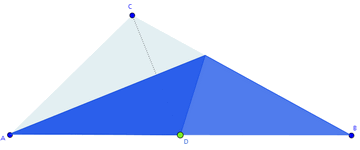
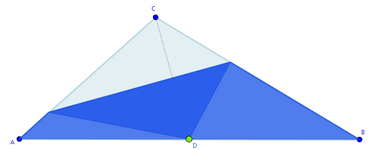
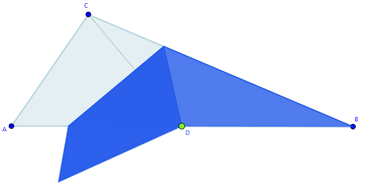
Supón que hemos recortado un triángulo de cartulina. Ahora vamos doblándolo hasta hacer coincidir uno de los vértices sobre el punto medio del lado opuesto:

Cuando completamos el doblado, es decir, cuando el vértice coincide con el punto medio del lado opuesto, según como sea el triángulo de partida, la figura que nos queda puede ser un triángulo, un cuadrilátero o un pentágono.

Aquí puedes ver un caso de cada una de esas situaciones finales:

Lo que te planteamos es una pequeña investigación: tienes que descubrir de qué depende que la figura final sea un triángulo, un cuadrilátero o un pentágono. Pero no te preocupes, no vas a tener que recortar un montón de triángulos y hacer pruebas: esa tarea la harás de un modo virtual, utilizando la aplicación que tienes más abajo.

Puedes mover los vértices del triángulo, los puntos A, B y C, para estudiar diferentes posibilidades. También puedes mover el punto verde, hasta que coincida con el punto D, que es el punto medio del lado AB.

Haz clic en el botón , situado en la parte superior derecha, para volver a los valores iniciales de la aplicación. 

Preguntas

1. Coloca el punto verde sobre D. A continuación mueve los puntos A, B y C como creas conveniente. Trata de lograr los diferentes casos: un triángulo, un cuadrilátero o un pentágono.

2. Mantén el punto verde sobre D. Coloca los puntos A y B de modo que el lado AB sea horizontal. Haz clic sobre la casilla de "Mostrar línea de pliegue". ¿Qué línea es esa, con respecto al segmento CD?

3. Mueve ahora el punto C. Observa la posición de la línea de pliegue cuando el resultado final es un triángulo, un cuadrilátero o un pentágono. ¿Puedes sacar alguna conclusión? Escríbela con tus palabras.

4. Activa ahora la casilla "Mostrar circunferencias". ¿Cuál es su centro? ¿Y su radio?

5. Mueve el punto C. ¿Qué ocurre cuando el punto C está situado sobre una circunferencia? ¿Y cuando está en el interior de las circunferencias? ¿Y si está fuera? Escribe tus conclusiones.

6. Es el momento de escribir las conclusiones finales: ¿Qué relación tiene la forma del triángulo con el resultado final del pliegue? ¿Cuándo se obtiene un triángulo? ¿Cuándo se obtiene un cuadrilátero? ¿Y un pentágono?