Ángulos entre paralelas

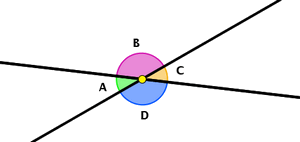
Dos rectas que se cortan decimos que son secantes. Al cortarse determinan 4 ángulos, como puedes ver en la figura. Pero esos ángulos están relacionados entre sí, de modo que si conociéramos cuanto mide uno de ellos, podríamos determinar inmediatamente los otros tres.

 

Según la posición de los ángulos con respecto a las rectas, reciben distintos nombres. Los llamamos ángulos opuestos por el vértice cuando comparten el vértice y los lados de uno son prolongación de los lados del otro, como sucede en los ángulos A y C. Decimos que son ángulos adyacentes cuando tienen el vértice y un lado común y los otros lados tales que uno es prolongación del otro. Son adyacentes, por ejemplo, el A y el B.

 

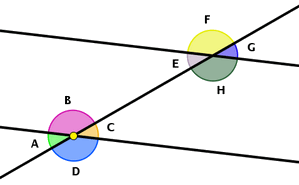
Cuando dos rectas paralelas son cortadas por otra recta, a la que llamaremos transversal se forman 8 ángulos, como puedes ver en la figura. Estos ocho ángulos también guardan una estrecha relación entre sí, de modo que, como en el caso anterior, en cuanto conocemos uno de ellos podemos averiguar lo que valen los demás.

 

La posición relativa de los ángulos con respecto a las rectas hace que esos ángulos reciban unos nombres específicos. Así, llamamos ángulos correspondientes a los que están situados al mismo lado de las paralelas y al mismo lado de la transversal. Son correspondientes, por ejemplo, el A y el E, o también el B y el F.

 

Llamamos ángulos alternos internos los que están a distinto lado de las paralelas y a distinto lado de la transversal. Son alternos internos el B y el H y también el C y el E.

 

Son ángulos alternos externos los que están en la parte exterior de las paralelas, a distinto lado de ellas y a distinto lado de la transversal.

 

En esta aplicación vamos a descubrir estas relaciones y a utilizarlas para resolver algunos problemas. Puedes cambiar la posición de las rectas moviendo los puntos amarillos que se destacan en ellas.

 

Vas a necesitar el transportador para medir los ángulos. Para utilizarlo debes activar la casilla Mostrar transportador. Para desplazar el transportador usa . Para girarlo, usa .

 

El deslizador rojo te permitirá situar una recta paralela a una de las rectas dadas, para estudiar las relaciones entre los ángulos formados por dos paralelas y una secante.

 

Al activar la casilla Mostrar el punto P sitúa un punto entre las rectas paralelas. Deberás mover el punto para situarlo según te propongan algunos de los problemas que vas a resolver. Tendrás la posibilidad de activar una ayuda que te servirá de pista para dichos problemas.

 

Lo sentimos, el applet de GeoGebra no pudo iniciarse. Por favor, asegúrate que en tu navegador se encuentra instalada y activada la versión 1.4.2 o superior de Java. (Haz clic aquí para instalar Java ahora.)

 

Preguntas

  1. ¿Cuáles son los pares de ángulos opuestos por el vértice? ¿Qué relación guardan entre sí los ángulos opuestos por el vértice? Compruébalo: mídelos con el transportador y comprueba los resultados. Cambia la posición de las rectas y repite la medición. ¿Se mantiene la relación entre ambos?

  2. ¿Qué pares de ángulos adyacentes observas? ¿Qué relación guardan entre sí los ángulos adyacentes? Compruébalo: mídelos con el transportador y comprueba los resultados. Cambia la posición de las rectas y repite la medición. ¿Se mantiene la relación entre ambos?

  3. Mueve las rectas para que el ángulo C mida 35º (ayúdate del transportador). ¿Cuánto miden los demás ángulos?

  4. Mueve el deslizador "Paralela" hacia la derecha. Observa los ángulos que aparecen. Señala todas las parejas de ángulos correspondientes que veas. ¿Qué relación guardan entre sí dos ángulos correspondientes? Utiliza el transportador para comprobar tus resultados. Cambia ahora la posición de las rectas (mueve alguno de los puntos amarillos). ¿Se mantiene la relación que has encontrado? Compruébalo con el transportador. Copia el dibujo en tu cuaderno y señala en él las parejas de ángulos correspondientes.

  5. Señala todas las parejas de ángulos alternos internos que veas. ¿Qué relación mantienen entre sí dos ángulos alternos internos? Compruébalo con el transportador. Cambia ahora la posición de las rectas (mueve alguno de los puntos amarillos). ¿Se mantiene la relación que has encontrado? Haz las mediciones oportunas y compruébalo. Copia el dibujo en tu cuaderno y señala en él las parejas de ángulos alternos internos.

  6. Señala todas las parejas de ángulos alternos externos que veas. ¿Qué relación mantienen entre sí dos ángulos alternos externos? Utiliza el transportador para comprobar tus resultados. Cambia ahora la posición de las rectas (mueve alguno de los puntos amarillos). ¿Se mantiene la relación que has encontrado? Haz las mediciones oportunas y compruébalo. Copia el dibujo en tu cuaderno y señala en él las parejas de ángulos alternos externos.

  7. Mueve las rectas para que el ángulo C mida 45º. ¿Cuánto miden los demás ángulos? Haz primero tus cálculos a partir de las relaciones que has encontrado en los apartados anteriores y, a continuación, comprueba los resultados midiendo con el transportador.

  8. Mueve ahora las rectas para que el ángulo H mida 64º. ¿Cuánto miden los demás ángulos? Haz primero tus cálculos a partir de las relaciones que has encontrado en los apartados anteriores y, a continuación, comprueba los resultados midiendo con el transportador.

  9. ¿Puedes conseguir que los 8 ángulos sean iguales? ¿Cuál será su valor en ese caso? ¿Por qué?

  10. ¿Puedes colocar las rectas de modo que el ángulo E mida 43º y el ángulo C mida 58º? Justifica tu respuesta y, en caso afirmativo, compruébalo con el transportador.

  11. Haz clic en para volver a la situación inicial. Mueve el deslizador "Paralela" al extremo derecho y activa la casilla "Mostrar el punto P". Mueve el punto P hasta que M=30º y N=15º. ¿Cuánto mide el ángulo T de color amarillo? Si necesitas alguna pista, activa la casilla "Ayuda".

  12. Si el ángulo M mide 25º y el ángulo T mide 68º, ¿cuánto mide el ángulo N? Haz el cálculo y, a continuación, comprueba con la aplicación tu resultado.