El número Pi, que se escribe 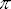, es el número de veces que la longitud de la circunferencia es más grande que su diámetro, es decir, es la razón entre la longitud de la circunferencia y su diámetro. Es uno de los números más importantes en Matemáticas, con aplicaciones en todas las Ciencias.

El valor aproximado de 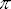es 3.1415926... Como ves no es un número entero, su valor ni siquiera equivale al de ninguna fracción, pues tiene infinitas cifras decimales no periódicas. Sin embargo, existe una fracción descubierta en el siglo V, y fácil de recordar (si comienzas por el denominador: 11-33-55) que aproxima el valor de 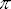con mucha precisión:

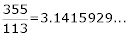
En la actualidad, se conocen más de dos billones de decimales exactos. Pero para la mayoría de los cálculos se suele usar la aproximación 3.1416. Para estimaciones por cálculo mental, puedes darle a 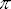el valor 3, siempre que conozcas que estás cometiendo un error que se puede ir acumulando si encadenas varios cálculos. Por ejemplo, una moneda de 2 cm de diámetro tendrá poco más de 6 cm de perímetro y una bala de calibre 9 mm tendrá poco más de 27 mm de circunferencia.

En esta actividad podrás comparar fácilmente el valor del diámetro de una circunferencia y el valor de su longitud, comprobando que en todas las ocasiones la razón entre ambas cantidades se mantiene constante e igual a .

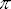Preguntas

1. Mantén el punto azul en el valor 4. ¿Cuál es el diámetro de la rueda? (La unidad es el centímetro.) El valor que has apuntado, ¿es exacto o aproximado?

2. Mueve el punto naranja hasta la posición más a la derecha que puedas. ¿Cuál es la longitud de la circunferencia, es decir, el perímetro de la rueda? El valor que has apuntado, ¿es exacto o aproximado?

3. Calcula la razón entre la longitud de la circunferencia (pregunta 2) y su diámetro (pregunta 1). ¿Por qué ese cálculo no da exactamente el valor de ?

4. Repite el cálculo anterior para distintos diámetros: 5, 3 y 2. ¿Obtienes el mismo resultado? ¿Por qué?

5. Coloca el punto azul en el valor 1. ¿Cuánto mide ahora la longitud de la circunferencia?