|
Preguntas
-
Antes de tocar nada, observa la imagen inicial (si ya has tocado algo, pulsa
el botón  Reiniciar). Se ve un icosaedro y su sombra. Las 20 caras del icosaedro son
triángulos equiláteros. Entonces, ¿cómo crees que es posible que su sombra
tenga forma pentagonal? (Pista: fíjate en el vértice más próximo al foco de
luz y en los vértices que se unen a él.)
Reiniciar). Se ve un icosaedro y su sombra. Las 20 caras del icosaedro son
triángulos equiláteros. Entonces, ¿cómo crees que es posible que su sombra
tenga forma pentagonal? (Pista: fíjate en el vértice más próximo al foco de
luz y en los vértices que se unen a él.)
-
Mueve el punto rojo (en la parte superior izquierda). ¿Qué efecto provoca?
¿Varía el contorno de la sombra?
-
Mueve el deslizador amarillo. ¿Qué efecto provoca? ¿Y al mover el deslizador
verde?
-
Mueve el foco de luz, ajustando también el deslizador amarillo si lo crees
conveniente. ¿Crees que habrá alguna posición en donde el contorno de la
sombra no sea ni un hexágono ni un pentágono?
-
Mueve el foco de luz a la derecha del icosaedro, ajusta su posición y
gira el punto rojo hasta conseguir que se muestre otra vez un contorno
pentagonal.
-
Mantén la escala en 1.9, sitúa el foco en la esquina inferior izquierda de la pantalla (a tope, lo más
que puedas) y mueve el punto rojo. ¿Qué sucede? ¿Por qué?
-
Desactiva las Caras, Vértices y Aristas del icosaedro y activa las
correspondientes casillas del cubo. Mueve el foco y el punto rojo hasta
conseguir que el contorno de la sombra sea un pentágono.
-
Mueve el foco y el punto rojo hasta conseguir que el contorno de la sombra sea
un cuadrilátero.
-
No podrás mover el foco y el punto rojo de forma que en la sombra solo se vean
4 de los puntos proyectados. ¿Por qué? ¿Dónde habría que colocar el foco para
conseguirlo?
-
Desactiva las Caras, Vértices y Aristas del cubo y activa las correspondientes
casillas del tetraedro. Mueve el foco y el punto rojo hasta conseguir que en
el contorno de la sombra solo sean visibles 3 Nodos, en vez de cuatro.
-
Desactiva las Caras, Vértices y Aristas del tetraedro y activa las
correspondientes casillas del octaedro. Mueve el foco y el punto rojo hasta
conseguir que en el contorno de la sombra solo sean visibles 5 Nodos, en vez
de seis.
-
Desactiva las Caras, Vértices y Aristas del octaedro y activa las
correspondientes casillas del dodecaedro. Mueve el foco hasta situarlo en la
misma posición (desde tu punto de vista) que el centro del dodecaedro y reduce
la apertura de la luz al mínimo. El punto del foco quedará situado justo en el
centro del círculo iluminado. Aunque se sigue proyectando el dodecaedro sobre
un plano situado detrás de él, al mover el punto rojo, ¿tienes alguna otra
percepción de la figura? Comprueba esa percepción con los otros poliedros,
aumentando o reduciendo la Escala si lo crees conveniente.
-
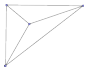
Vamos ahora a preparar las proyecciones para facilitar las cuentas. Activa Vértices y
Aristas del tetraedro y la casilla Grafo. Aparecerá un gráfico
("grafo") de puntos unidos por líneas, equivalente a la proyección del
tetraedro. Comprueba que, efectivamente, de cada Nodo salen tantas Líneas como
Aristas salen de cada Vértice del icosaedro. Mueve el Nodo D hasta el interior del triángulo
ABC, así ningún par de Líneas se cortarán. ¿Cuántas Regiones hay? (No olvides
que la superficie completa, el triángulo ABC, forma también una región.)
-
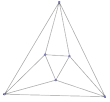
Desactiva Vértices y Aristas del tetraedro y activa Vértices y
Aristas del octaedro. Mueve los Nodos B, D y F hasta el interior del triángulo
ACE, así ningún par de Líneas se cortarán. ¿Cuántas Regiones hay? (No olvides
que la superficie completa, el triángulo ACE, forma también una región.)
-
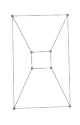
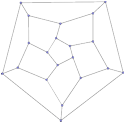
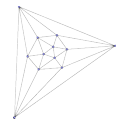
Realiza el mismo proceso con los grafo de los demás poliedros. Ten en cuenta
que a medida que el número de Nodos aumenta te resultará cada vez más difícil
lograr que ningún par de Líneas se corten, pero siempre es posible
conseguirlo. El método general para lograrlo es similar a lo realizado con el
octaedro: elige una región y coloca el resto de los Nodos dentro.
-
Una vez preparados los grafos, ya podemos contar. Primero, comprueba la
igualdad "Regiones + Nodos - Líneas = 2" en cada uno de los grafos.
-
Visualiza el grafo del tetraedro. El camino BADC pasa una sola vez por cada
vértice. ¿Cuántos caminos distintos puedes contar que pasen una sola vez por
los cuatro vértices? Escribe unos cuantos caminos y después busca la manera de
contarlos sin tener que escribirlos todos uno por uno.
-
Hagamos la cuenta más fácil, dividiendo el trabajo en partes. ¿De cuántas
formas distintas podemos recorrer el primer tramo, es decir, la primera Línea?
Por ejemplo, una forma es AB, otra BA, otra AC, otra CA, etc.
-
Ahora elige una de esas primeras Líneas (por ejemplo AB) y a partir de ahí
cuenta cuántos caminos hay que empiecen "AB...". No son muchos... ¿Todos ellos
permiten "cerrar" el recorrido regresando al Nodo inicial (es decir, realizar
un circuito)?
-
A partir de las respuestas a las dos preguntas anteriores,
¿cuántos caminos distintos puedes contar en total que pasen una sola vez por
los 4
vértices del tetraedro?
-
Visualiza el grafo del octaedro. ¿De cuántas formas distintas podemos
recorrer el primer tramo, es decir, la primera Línea? Por ejemplo, una forma
es AB, otra BA, otra AC, otra CA, etc.
-
Ahora elige una de esas primeras Líneas (por ejemplo AB) y a partir de ahí
cuenta cuántos caminos hay que empiecen "AB...". No son muchos, pero
un diagrama de
árbol te puede resultar muy útil. ¿Todos ellos permiten "cerrar" el recorrido
regresando al Nodo inicial (es decir, realizar un "circuito")?
-
A partir de las respuestas a las dos preguntas anteriores,
¿cuántos caminos distintos puedes contar en total que pasen una sola vez por
los 6
vértices del octaedro?
-
Sigue la misma estrategia para averiguar cuántos caminos distintos pasan una
sola vez por los 8 vértices del cubo y cuántos circuitos pueden realizarse.
-
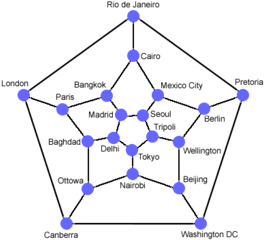
Hacia 1850 el matemático W. R. Hamilton patentó un juego que llamó Viaje
por el Mundo. Consistía en encontrar un circuito que pasase por 20
ciudades situadas en los Nodos del grafo del dodecaedro (que es equivalente a
un recorrido por los 20 vértices del dodecaedro). Visualiza el grafo del
dodecaedro. ¿Puedes encontrar una solución? Si activas "Cadena" podrás
ayudarte de la cadena roja para señalar el recorrido.

-
Visualiza el grafo del icosaedro. Encuentra un circuito "hamiltoniano", es
decir, que pase por todos los Nodos una sola vez.
-
Veamos algo que parece mucho más difícil pero que gracias a los grafos podemos
resolver rápidamente. ¿Cuántos caminos distintos recorren las 30 Aristas del
dodecaedro una sola vez? En vez de contestar directamente, intenta primero el
caso del tetraedro.
-
Observa que, para recorrer todas las Líneas, los Nodos intermedios (todos
excepto el inicial y el final) tienen que tener un número par de Líneas
conectadas a ellos (la mitad para poder acceder y la otra mitad para poder
salir). ¿Cuál es el único poliedro que cumple este requisito?
-
Si todos los Nodos tienen un número par de Líneas conectadas a ellos entonces
es posible realizar un circuito por las aristas, es decir, recorrer todas las
aristas volviendo al Nodo inicial. Encuentra un circuito de este tipo en el
octaedro, ayudándote de la Cadena.
-
Realiza una estimación de cuántos circuitos distintos crees que,
aproximadamente, pueden formarse recorriendo todas las aristas del octaedro
una sola vez.
|






