3-RPR : the forward kinematic problem

A 3-RPR planar manipulator consists of a platform moving in a plane and linked to the base via three legs A_iB_i , each one consisting of:

• a passive revolute joint (R) centered at A_i ,
• an actuated prismatic joint (P) controlling the length of the leg A_iB_i ,
• a passive revolute joint (R) centered at B_i .

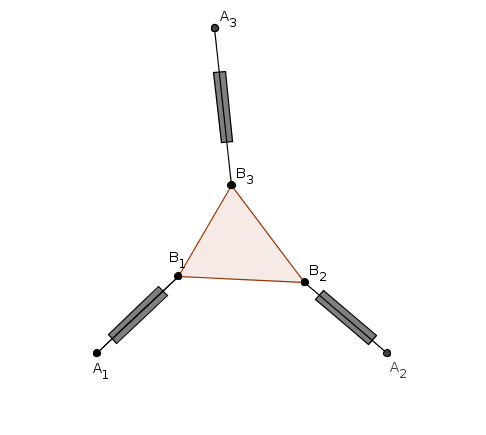
If the position of the platform B₁B₂B₃ is known, then the lengths l_i of the legs A_iB_i are known. The forward kinematic problem is the following : how many positions of the platform correspond to given (l₁, l₂, l₃) ?

If the lengths of the legs A₁B₁ and A₂B₂ are fixed to l₁ and l₂ and the leg A₃B₃ is cut, see what happens:

The third vertex of the moving platform describes a curve which is a 3-cyclic sextic (3-cyclic means that the cyclic points belong to the curve with multiplicity 3). On the animation, the leg A₁B₁ rotates. To each position of this leg correspond at most  two possible positions of the leg A₂B₂ : one with "knee B₂ up" (this mode is indicated in green) and the other with "knee B'₂ down" (in red). The corresponding points B₃ and B'₃ are actually on the same sextic, which has two connected components in the default setting of the applet. But you can move the point A₂ to see how the shape of the curve evolves and obtain eventually a situation where the sextic has only one connected component (with two segments of different colors).

The number of intersections of the sextic with the circle of center A₃ and radius l₃ is the number of solutions to the forward kinematic problem. You can move the point A₃, change the radius l₃ and check that the number of intersections is generically 0, 2, 4 or 6.

Reference : J-P. Merlet, Parallel Robots, Springer

Michel Coste, created avec GeoGebra