|
|
► 6. Problemas dirigidos
► 6.5 Viviani
Objetivos
Se pretende ejemplificar el uso de GeoGebra como ayuda en la
exploración, descubrimiento o comprobación de invariantes geométricos. Hemos
elegido uno de los más sencillos, conocido como teorema de Viviani
![]() .
.
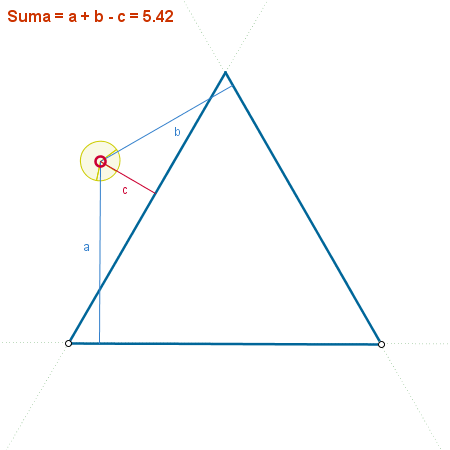
Según el teorema de Viviani, "en todo triángulo equilátero la suma de las tres distancias de un punto interior a los lados es constante". Dado que desde un vértice esa suma es, evidentemente, la longitud de la altura del triángulo, esta será la constante.
Si asignamos un signo a cada distancia, según se encuentre el punto en uno u otro semiplano a cada lado del lado (valga la redundancia), el teorema es válido para todos los puntos del plano, ya sean interiores, exteriores o fronterizos.
Herramientas
Usaremos el comando Texto para crear un texto dinámico, y los comandos Si y Elemento para tratar la información. También veremos un ejemplo de cómo operar con listas. Además usaremos las siguientes herramientas.
|
|
Punto |
|
Intersección |
|
Recta |
|
|
Segmento |
|
Perpendicular |
|
Polígono regular |
|
|
Ángulo | ||||
Construcción paso a paso
Antes de empezar, puede ser buena idea echar un vistazo al "Ejemplo de construcción" que se encuentra en esta página. Incluso podemos ayudarnos de la Barra de Navegación para realizar un rápido recorrido por los pasos.
Preparamos el escenario.
|
|
Construimos la figura.
|
|
Si usamos la construcción para comprobar o demostrar el teorema (no para descubrirlo), añadimos un texto dinámico que muestre el resultado.
|
|
Observemos que "test" es una lista, creada al restar la lista de ángulos de una constante (180°) y tomar el signo de esa diferencia.
Ejemplo de construcción
Comentarios
Dependiendo del nivel de conocimientos y experiencia de nuestros alumnos podemos usar esta construcción u otras similares para:
a) Comprobar que se cumple el teorema.
b) Invitar a que descubran el teorema, sugiriendo que deben buscar una medida invariante.
c) Invitar a que descubran el teorema, construyendo ellos mismos la figura.
d) Invitar a que demuestren el teorema, añadiendo si es preciso algunos elementos auxiliares a la construcción.
![]() Investigación:
Investigación:
- ¿Por qué se produce esta constancia de la suma de las distancias? ¿Es difícil demostrar el teorema de Viviani?
- En el apartado Otros modelos podemos encontrar la generalización del teorema de Viviani a cualquier polígono equiangular (no necesariamente regular). ¿Se puede generalizar la demostración anterior a este caso general?