Manual
Imágenes
Inicio
  |
► 6. Propuestas sencillas de construcción
► 6.3 Colores
Objetivos
Usaremos la propiedad Color Dinámico para visualizar fácilmente lugares geométricos desconocidos, siempre que sepamos expresar la condición que deben cumplir los puntos del mismo.
Este modo de empleo del Color Dinámico es realmente potente. Simplemente "barriendo" la pantalla el lugar geométrico aparece, como por arte de magia, ante nuestros ojos.
El Color Dinámico
La propiedad Color Dinámico asigna al objeto tres valores numéricos, cada uno de ellos variable entre 0 y 1, que corresponden a la intensidad de rojo, verde y azul presentes en su color-luz combinado.
Para desactivar esta propiedad se debe usar el botón
situado a la derecha
del código RGB (red, green, blue). En tal caso, el color del objeto será el establecido en la
Color
del cuadro de diálogo Propiedades del objeto. Es la opción predefinida al crear
un objeto nuevo.
En la siguiente tabla se puede apreciar (agrupados por complementarios) el resultado de la elección de algunos colores básicos.
Rojo Verde Azul Color Nombre 0 0 0 Negro 1 1 1 Blanco 0.33 0.33 0.33 Gris oscuro 0.67 0.67 0.67 Gris claro 1 0 0 Rojo 0 1 1 Cian 0 1 0 Verde 1 0 1 Magenta 0 0 1 Azul 1 1 0 Amarillo
Cuando un valor numérico "k" no esté entre 0 y 1, GeoGebra sigue la siguiente norma:
1) Si el valor numérico no está entre 0 y 2, divide entre 2 y se queda con el resto.
2) Si el valor numérico "k" obtenido (o el resto de dividir entre 2) está entre 1 y 2, toma "2 - k".
El motivo de este comportamiento es evitar cambios bruscos de color entre dos valores numéricos próximos.
Por ejemplo, la siguiente imagen corresponde al rastro de color que ha dejado una circunferencia al girar alrededor de un punto.
Los pasos de construcción son:
Nº Nombre Definición Comando 1 Punto A 2 Circunferencia c Circunferencia con centro A y radio 4 Circunferencia[A, 4] 3 Punto B Punto en c Punto[c] 4 Circunferencia d Circunferencia con centro B y radio 4 Circunferencia[B, 4]
Una vez construida la circunferencia "d", en su propiedad de Color Dinámico introducimos los valores:
Rojo: x(B) Verde: y(B) Azul: x(B)-y(B)
donde x(B) es la abscisa de B e y(B) es la ordenada de B. Por último, activamos el rastro de la circunferencia "d" y movemos suavemente su centro, el punto B, que girará alrededor del punto A. Recordemos que para borrar ese rastro debemos pulsar Ctrl F (la F de Fresh).
La construcción
Vamos a resolver el mismo problema que en la sección anterior, usando ahora el método del Color Dinámico. Tenemos dos puntos fijos A y B y un punto libre C. Queremos conocer dónde están las posiciones de los puntos que distan de B el doble que de A.
Para abreviar la escritura, llamaremos "b" a la distancia de C a B y "a" al doble de la distancia de C a A. En la Barra de Entrada escribimos (se puede usar Ctrl C y Ctrl V para copiar y pegar la selección desde aquí):
b = Distancia[C,B]
a = 2 Distancia[C,A]
Queremos averiguar para qué posiciones de C se cumplirá "b = a".
Para ello, establecemos como Propiedad de Color Dinámico del punto C:
la expresión a/b en el color Rojo,
la expresión b/a en el color Verde y
la expresión 1+a-b en el color Azul.
Observemos que cuando "b" sea igual a "a", y solamente en ese caso, las tres expresiones valdrán 1, así que el color resultante será blanco.
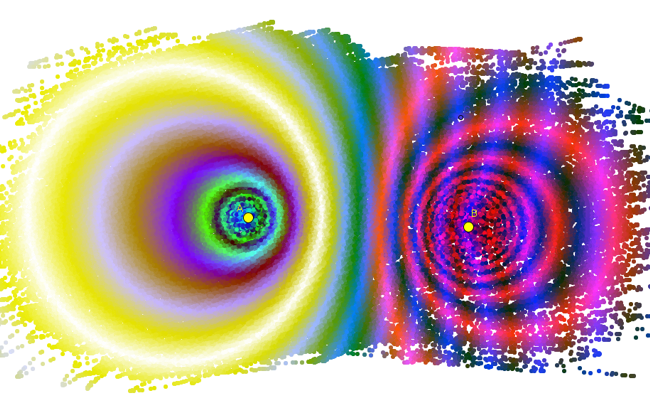
Ahora solo tenemos que activar el rastro del punto C y moverlo por la pantalla, buscando las zonas más próximas al blanco. Después de algunos "barridos" obtendremos una imagen similar a esta:
Hemos destacado los puntos A y B, en tamaño mayor y color amarillo, A a la izquierda y B a la derecha. Como un halo fantasma, la circunferencia blanca nos señala la solución del problema.
Propuesta de trabajo
Resolver con este método el problema de encontrar todos las posiciones que disten dos unidades más de B que de A:
b = Distancia[C,B]
a = 2+Distancia[C,A]
Comentarios
El color dinámico nos conduce rápidamente hacia el descubrimiento del lugar geométrico buscado. Los tonos claros nos indican la posible cercanía del blanco, nuestro objetivo, algo así como en el juego del "frío o caliente". De esta forma, las distintas luminosidades nos van facilitando cada vez más información sobre dónde se encontrará el lugar buscado. Además de útiles, las imágenes que se obtienen con este método a menudo son muy bellas, pues las propiedades de las expresiones y operaciones matemáticas quedan reflejadas en las formas y colores obtenidos.
Investigación:
- Dados los valores "a" y "b", existe una infinidad de expresiones que toman el valor 1 cuando los dos valores sean iguales. Considerando que el signo ^ indica "elevado a", sqrt() indica "raíz cuadrada de", y abs() indica "valor absoluto de", algunas de ellas son:
a/b, b/a, 1+a-b, 1+b-a, (a/b)^2, sqrt(a/b), 2^-abs(a-b), (3b-2a)/(2a-b), etc.
Es interesante y divertido probar a variar estas expresiones en el color dinámico y observar el resultado obtenido en cada caso. Por ejemplo, la combinación:
Rojo: a/b Verde: (3b-2a)/(2a-b) Azul: 2^-abs(a-b)
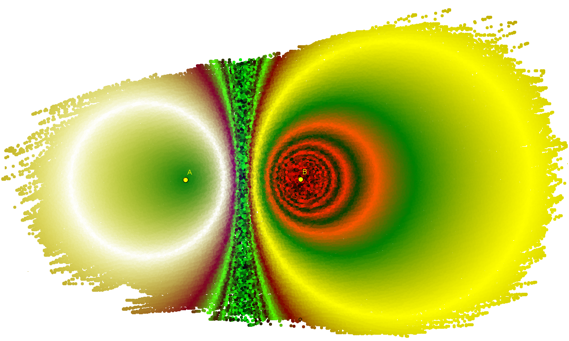
produce para el problema anterior la imagen:
mientras que si definimos k = sqrt((2a-b)(2b-a)), las expresiones:
Rojo: k/b Verde: k/a Azul: k/sqrt(a b)
provocan la aparición de la imagen:
