Si colocamos una parábola de forma que su eje de simetría sea una vertical entonces cada recta vertical cortará a la parábola en un solo punto. Esto permite considerar a la parábola como la gráfica correspondiente a alguna función. Pero... ¿qué función es esa?

En esta actividad introducimos una parábola particular en el sistema de coordenadas, colocando el vértice V en el origen (0, 0) y el foco en (0, 1/4). En esa posición podemos averiguar fácilmente la relación de dependencia de la ordenada Y respecto a la abscisa X de todos y cada uno de sus puntos, es decir, podemos hallar su ecuación.

A partir de esa parábola básica, como sabemos que todas las parábolas con el mismo vértice y eje son homólogas respecto a ese vértice, encontraremos rápidamente la ecuación de cualquier otra parábola de eje vertical con vértice en el origen.

Veremos que cualquier parábola con vértice en el origen y eje vertical queda determinada por un solo número (parámetro) "a".

Preguntas

1. Observa detenidamente la figura. La parábola tiene vértice en el origen de coordenadas (0, 0) y su foco en el punto (0, 1/4) del eje de ordenadas. Puedes mover el punto P sobre la parábola. ¿Cuál es el valor del parámetro p de esa parábola? ¿Cuánto mide el lado recto?

2. ¿Cuál es la ecuación de la recta directriz de esa parábola?

3. Los triángulos rectángulos VFM y NDM son congruentes. ¿Por qué?

4. En función de la abscisa de P, "X", ¿cuáles son las coordenadas de N y M?

5. ¿Cuáles son las coordenadas de D?

6. Escribe, en función de las coordenadas de P, X e Y, el valor de las longitudes de los segmentos: VF, NP, NM y VM.

7. Los dos ángulos de color violeta son iguales. ¿Por qué?

8. Los dos triángulos rectángulos de color violeta son semejantes. ¿Por qué?

9. Como los triángulos son semejantes, tenemos la igualdad NP/NM = VM/VF. ¿Por qué?

10. La anterior igualdad se puede escribir como VF NP = NM VM. Sustituye VF, NP, NM y VM por su valor en función de X e Y. Simplifica la igualdad para llegar a la ecuación de esa parábola: Y = X².

11. Mueve el punto A y comprueba en distintas posiciones que sus coordenadas cumplen la relación anterior, es decir, su ordenada siempre coincide con el cuadrado de la abscisa.

12. Observa el triángulo PNM bajo la recta tangente a la parábola en P. En función de la abscisa X de P, y teniendo en cuenta que Y = X², ¿cuál es la pendiente de esa recta tangente en P?

13. La igualdad Y = X² representa un equilibrio, un estado fronterizo entre dos regiones del plano: todos los puntos (X, Y) para los cuales Y < X², y todos los puntos (X, Y) para los cuales Y > X². ¿Dónde se sitúan cada una de esas dos regiones del plano?

14. Sabemos que cualquier parábola con vértice en el origen y foco en el eje de ordenadas será homóloga a la parábola básica Y = X². Activa la casilla Homotecia. Al aplicar una homotecia centrada en el vértice V con factor k, obtenemos una nueva parábola con foco en F'.  Las coordenadas de F' son (0, k/4). ¿Por qué? ¿Cuál es el valor del parámetro p de la nueva parábola?

15. Cada punto P (X, Y) de la parábola Y = X² tendrá un homólogo P' (x, y) = (kX, kY). Ahora nos interesa averiguar cuál es la relación entre las dos coordenadas de P'.
    
    Si la homotecia con factor k transforma P en P', la homotecia con factor a=1/k transformará P' en P. Así que si (x, y) son las dos coordenadas de P', tenemos que las coordenadas de P serán (X, Y) = (ax, ay).
    
    Como se cumple que Y = X², tenemos que ay = (ax)². Simplificando esta expresión obtenemos la ecuación de cualquier parábola con vértice en el origen: y = a  x².
    
    La relación del coeficiente "a" con el parámetro p de la parábola será a = 1/k = 1/(2p), cuando "a" sea positivo y a = 1/k = -1/(2p) cuando "a" sea negativo. ¿Por qué? Observa que en ambos casos el valor absoluto de "a" es el inverso de la longitud del lado recto, mientras que su signo indica la orientación de la parábola.

16. Basta ver la ecuación y = a x² para poder afirmar, sin necesidad de ver la gráfica, que representa a una función par. ¿Por qué?

17. Observa el triángulo azul bajo la recta tangente a la parábola en P'. En función de la abscisa x de P', y teniendo en cuenta que y = a x², ¿cuál es la pendiente de esa recta tangente en P?

18. La igualdad y = a x² representa un equilibrio, un estado fronterizo entre dos regiones del plano: todos los puntos (x, y) para los cuales y < a x², y todos los puntos (x, y) para los cuales y > a x². ¿Dónde se sitúan cada una de esas dos regiones del plano?

19. Asigna a k el valor k=2. ¿Qué relación existe entre las dos parábolas que aparecen en la aplicación? ¿Cuál es la ecuación de cada una?

20. Mueve el deslizador hasta el valor k=-1. ¿Qué relación existe ahora entre las dos parábolas? ¿Cuál es la ecuación de cada una?

21. ¿Cuál será la ecuación de una parábola con vértice en el origen y foco en (0, 1)?

22. ¿Cuál será la ecuación de una parábola con vértice en el origen y foco en (0, -1)?

23. ¿Cuál será la ecuación de una parábola con vértice en el origen y directriz y = 0.5?

24. ¿Cuál será la ecuación de una parábola con vértice en el origen y directriz y = -0.5?

25. ¿Cuál es el valor del parámetro p de la parábola de ecuación y = 2x²? ¿Dónde está su foco? ¿Cuál es la ecuación de su recta directriz?

26. ¿Cuál es el valor del parámetro p de la parábola de ecuación y = -2x²? ¿Dónde está su foco? ¿Cuál es la ecuación de su recta directriz?

Nota: Si te gusta manipular ecuaciones, puedes intentar una forma más directa (pero con menos conexiones) de llegar a la ecuación y = a  x² transformando la ecuación que debe cumplir, como lugar geométrico, toda parábola con vértice en el origen y foco en un punto F (0, f) del eje de ordenadas: la distancia de cualquier punto P (x, y) a F debe coincidir con la distancia de P a la directriz y = -f, así que tenemos que:

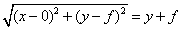
Elevando al cuadrado los dos miembros, desarrollando los cuadrados de la suma y diferencia, y simplificando, alcanzamos la ecuación:

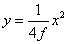
que se puede escribir como  y = a  x² simplemente llamando "a" al coeficiente 1/(4f).