En esta actividad comprobaremos que todas las hipérbolas con la misma excentricidad tienen la misma forma, es decir, son semejantes.

Para ello recurriremos a la homotecia, una transformación en la que dado un punto K del plano, aleja o acerca en un mismo factor (k) todos los demás puntos a K. Para factores positivos, la homotecia provoca un zoom de acercamiento o alejamiento centrado en K, un cambio de la escala con la que vemos las cosas. Para factores negativos, provoca, además, una inversión de la figura.

Naturalmente, ninguna figura va a cambiar de forma solo por acercarnos o alejarnos de ella, o por darle la vuelta, así que cualquier homotecia conserva la forma. Por ejemplo, si aplicamos una homotecia a un rectángulo obtendremos otro tal vez mayor, tal vez igual o tal vez menor, pero siempre semejante.

Preguntas

1. En la construcción puedes variar la posición de la directriz, del foco F y del punto E que determina la excentricidad de la hipérbola. Activa la casilla Rectángulo y la casilla Homotecia para ver el resultado de aplicar una homotecia con centro C, y con factor una constante k, a un rectángulo con un vértice en el punto E, obteniendo otro rectángulo donde el vértice correspondiente (punto homólogo de E) es el punto E'. Mueve el punto blanco del rectángulo con vértice en E. Para k = 2, ¿qué relación hay entre las distancias CE' y CE?

2. Cada par de lados correspondientes (cada par de lados homólogos) en ambos rectángulos, junto con el punto C, forman un par de triángulos semejantes, uno dentro del otro. ¿Qué famoso teorema de geometría clásica garantiza esa semejanza?

3. De la semejanza de esos triángulos podemos deducir que los dos rectángulos verdes que aparecen en la construcción son semejantes, es decir, sus lados correspondientes (sus lados homólogos) son proporcionales. ¿Por qué? (También puedes imaginar la figura como un proyector de cine, como se hace en esta actividad.)

4. Varía el valor del factor k. Observando la posición de E', intenta explicar qué sucede cuando k toma valores negativos.

5. ¿Para qué valores del factor k el rectángulo con vértice en E' será de menor tamaño que el rectángulo con vértice en E?

6. Haz clic en el botón Reiniciar. Activa la casilla Circunferencia y la casilla Homotecia para ver el resultado de aplicar una homotecia de factor k con centro C a una circunferencia centrada en O, con la misma curvatura que la hipérbola en su vértice (activa temporalmente la casilla Hipérbola para apreciarlo y vuelve a desactivarla), obteniendo otra circunferencia con la misma curvatura que la hipérbola homóloga en su vértice. Mueve el punto blanco de la circunferencia centrada en O. Para k = 2, ¿qué relación hay entre las distancias CO' y CO?

7. En esa homotecia, ¿cuál es el punto homólogo de C?

8. ¿Qué le sucede a la circunferencia cuando el factor k toma valores negativos?

9. De esta construcción podemos deducir que todas las circunferencias son semejantes, es decir, tienen la misma forma. ¿Por qué?
   
   Nota: No debes confundir forma con curvatura. Todas las circunferencias tienen la misma forma, pero su curvatura es inversamente proporcional a su radio. Cuanto mayor sea el radio menor será su curvatura. Por eso la Tierra nos parece plana cuando estamos en su superficie: su radio es muy grande comparado con la altura de nuestros ojos sobre el suelo, así que no parece curvarse. Sin embargo, un astronauta puede apreciar su curvatura al alejarse suficientemente de su superficie.

10. Pulsa en Reiniciar. Activa la casilla Hipérbola y la casilla Homotecia para ver el resultado de aplicar una homotecia de factor k con centro C a la hipérbola determinada por el foco F y la directriz d, obteniendo otra hipérbola con foco en F' (punto homólogo de F) y directriz en d' (recta homóloga de d, dibujada discontinua). Para k = 2, ¿qué relación hay entre las distancias CF' y CF? ¿Y entre las distancias de C a d y de C a d'?

11. ¿Qué le sucede a la hipérbola cuando el factor k toma valores negativos? En particular, ¿qué sucede cuando k = -1?

12. De esta construcción se puede deducir que todas las hipérbolas con el mismo centro, eje principal y excentricidad son homólogas. ¿Por qué?
    
    Observa que, en particular, esto significa que todas las hipérbolas equiláteras con el mismo centro y eje principal son homólogas, pues todas ellas tienen la misma excentricidad ().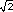

13. También podemos deducir que todas las hipérbolas con la misma excentricidad son semejantes, es decir, tienen la misma forma. ¿Por qué?
    
    Nota: Al igual que pasa con las circunferencias, todas las hipérbolas con la misma excentricidad tienen la misma forma, pero su curvatura varía según sea el parámetro focal p. Cuanto mayor sea el valor de p menor será su curvatura. Por eso nos da la impresión de que los brazos de la hipérbola "se cierran o se abren más o menos" cuando variamos la distancia entre el foco y la directriz, es decir, el parámetro p.

14. Pulsa en Reiniciar. Activa las casillas Rectángulo, Circunferencia, Hipérbola y "Efecto zoom" para ver el efecto resultante de aplicar una homotecia con centro C en donde el factor k varía gradualmente. Mueve el deslizador del factor k. Da la impresión de que los brazos de la hipérbola se cierran o se abren, pero en realidad, como has podido comprobar, no es más que un efecto "zoom" producido al aproximar o alejar los demás puntos del vértice C como consecuencia de aplicar una homotecia de factor k. Después de aplicar una homotecia de factor 2 a una figura, ¿cómo la podrías devolver a su tamaño original?