Hasta mediados del siglo XX se creía que todos los conjuntos de teselas (una o más) que podían formar mosaicos aperiódicos podían recolocarse formando también mosaicos periódicos.

En 1964 se encontró un conjunto que teselaba el plano solo de forma aperiódica. Lo malo es que el número de azulejos necesario era muy grande: ¡exactamente 20.426!

Diez años más tarde, el físico matemático Sir Roger Penrose consiguió reducir ese número a solo 2 azulejos, conocidos como Dardo y Cometa.

Hoy por hoy sigue siendo un problema abierto saber si puede existir un único azulejo capaz de teselar solo de manera no periódica.

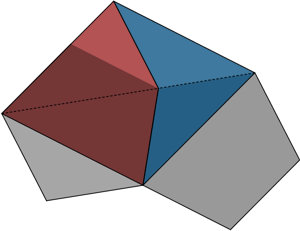
La construcción del Dardo y la Cometa es muy simple, a partir de dos pentágonos adosados, recortamos por la línea discontinua y reflejamos sobre ella:

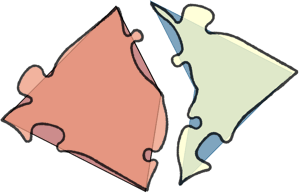
Como podemos observar, El Dardo y la Cometa se pueden unir para formar un paralelogramo (más precisamente, un rombo de lado la diagonal del pentágono), y sabemos que cualquier paralelogramo tesela periódicamente el plano. Para evitarlo, se añaden muescas y salientes (ver el método de quita y pon) en los lados que impiden esa forma de unir un Dardo y una Cometa.

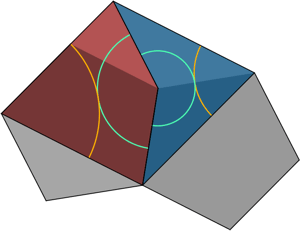
Pero esas muescas afean el mosaico. Afortunadamente, pueden ser sustituidas por arcos pintados en cada azulejo, a dos colores, de tal forma que las muescas solo coincidirían cuando un arco conecta con otro del mismo color.

Así que basta imponer la condición de que los extremos de los arcos de cada color deben coincidir para evitar que se adose un Dardo a una Cometa formando el rombo.