Ortocentro

Ortocentro.

El triángulo abc es el triángulo órtico del triángulo ABC.

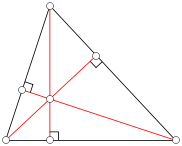
Se denomina ortocentro (símbolo H) al punto donde se cortan las tres alturas de un triángulo. Este no es un hecho trivial, pues tres rectas cualquiera, tomadas a pares, podrían intersectarse en tres puntos diferentes, pero en el caso de las alturas de un triángulo dado, puede demostrarse que se intersectan en un solo punto, es decir, en el ortocentro.

El nombre deriva del término griego orto, que quiere decir recto, en referencia al ángulo formado entre las bases y las alturas.^[1]

El ortocentro se encuentra dentro del triángulo si éste es acutángulo, coincide con el vértice del ángulo recto si es rectángulo, y se halla fuera del triángulo si es obtusángulo.

El ortocentro es el incentro del triángulo órtico (como se observa en la figura). El triángulo órtico de un triángulo es el que tiene por vértices los pies de las tres alturas de éste, es decir, las proyecciones de los vértices sobre los lados..

Véase también

• Recta de Euler
• Circuncentro
• Baricentro

Referencias

Enlaces externos

• Weisstein, Eric W., «Altitude» (en inglés), MathWorld, Wolfram Research, http://mathworld.wolfram.com/Altitude.html .
• Weisstein, Eric W., «Orthocenter» (en inglés), MathWorld, Wolfram Research, http://mathworld.wolfram.com/Orthocenter.html .