|
Resumen
GeoGebra permite representar rápidamente conjuntos de objetos matemáticos,
como familias de funciones (a partir de uno o más parámetros) o familias de
curvas y superficies (a partir de sus parametrizaciones). También nos
permite perfilar imágenes o recorridos dados mediante poligonales y splines.
Pero, además, gracias a la incorporación de los guiones, podemos crear
escenarios en los que los objetos interactúen, ya sea buscando por sí mismos
posiciones óptimas según el criterio deseado, ya sea adecuando su
comportamiento a la posición de los demás objetos. Activando el rastro de
algunos puntos, podemos visualizar su comportamiento en estos sistemas
dinámicos, lo que favorece su análisis y comprensión.
En las construcciones que presentaré resultará clave la noción de "movimiento", tanto desde el
punto de vista matemático (vectores y parámetros) como de uso de GeoGebra (deslizadores, rastros, animaciones automáticas
y guiones de GeoGebra).
Además, se ofrecerá a los profesores información técnica no documentada
sobre parametrizaciones de los lugares geométricos empleados por GeoGebra.
Información
Procedimientos pautados
 procedimientos
pautados.ggb
Para exponer algunos procedimientos usados en GeoGebra, resulta muy útil
disponer de una plantilla ya preparada, como la que se muestra aquí, en la
que lo único a variar en cada caso sea la lista de textos con las
instrucciones. Los objetos usados por la propia plantilla son auxiliares, para ocultarlos de la
Vista Algebraica.
Nota: Para
saltar de línea en un texto de la lista de instrucciones se usa \\n.
Contenidos relevantes
Las
construcciones hacen uso de diversos comandos y herramientas de GeoGebra.
Sin embargo, algunos tipos de objetos resultan de especial interés por su
versatilidad y funcionalidad:
• Puntos,
vectores y curvas paramétricas.
• Deslizadores y animaciones.
• Listas y secuencias. La hoja de cálculo.
• Guiones básicos. Guiones en deslizadores.
En este documento (PDF,
DOC)
se puede consultar información técnica detallada para los profesores sobre
las parametrizaciones que rigen los objetos (rectas, cónicas, funciones,
listas...) de GeoGebra.
Alugnos ejemplos prácticos de la utilidad de las parametrizaciones
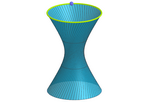
circuferencias e hiperboloide reglado
En este ejemplo, parametrizando las circunferencias de las bases, podemos conseguir la superficie
reglada simplemente retorciendo (es decir, desfasando) la circunferencia
superior respecto a la inferior.
 estadio.ggb
Gracias a las parametrizaciones, podemos conseguir rápidamente curvas y
superficies sofisticadas, como estas superelipses de un estadio. La clave
está en definir la superficie entre dos curvas paramétricas, tal y como se
muestra en esta construcción y en la anterior.
funciones
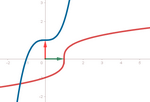
vectoriales.ggb
Si redefinimos vectorialmente una función f(x) como O + t i + f(t)
j, donde {O, i, j} constituyen el sistema
referencial, basta intercambiar de posición los vectores i, j
para obtener la gráfica de la función inversa (cuyo dominio tal vez se
deba restringir, según los casos, para que sea efectivamente una función).
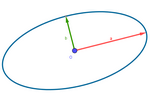
elipse vectorial.ggb
También resulta mucho más sencilla la manipulación de objetos geométricos
como las elipses si las definimos
vectorialmente sobre un sistema referencial relativo. De hecho, es lo que
hace el propio programa GeoGebra (ver PDF anterior).
Representaciones matemáticas y estética
Vista 2D
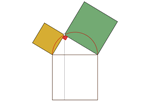
teorema de Pitágoras: una
comprobación dinámica
Una misma construcción puede ser útil para más de un fin. En esta
construcción se visualizan tres teoremas: el segundo teorema de Tales
(todo ángulo inscrito que abarque un diámetro es recto), el teorema del
cateto (el cateto es la media proporcional de la hipotenusa y su
proyección sobre ella) y el teorema de Pitágoras.
La construcción anterior es un ejemplo de cómo usar GeoGebra para
comprobar visualmente una relación. Pero también podemos crear
construcciones cuya visualización ayuden a demostrar tal relación.
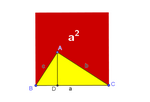
teorema de Pitágoras: una
demostración simple y profunda
Antes de mostrarles esta construcción a mis alumnos, suelo predisponerlos
con la siguiente pregunta a debate: La fracción que Asturias ocupa en un
mapa de toda España, ¿depende de la escala del mapa, es decir, varía al
hacer una ampliación o reducción del mapa?
Demostración:
En la figura, los tres triángulos rectángulos son semejantes. Por tanto,
ocupan la misma proporción (k) de cada cuadrado construido sobre sus
hipotenusas. Como el triángulo mayor es la suma de los otros dos, los
cuadrados correspondientes guardan la misma relación.∎
Vista 3D
Esta vista, sola o en combinación con la Vista Gráfica, añade más
posibilidades de representación y, por lo tanto, nuevos retos estéticos.
Veamos algunos ejemplos.
poste de barbero.ggb
No todo el mundo percibe igual las mismas imágenes, incluso aunque sean
representaciones animadas en un escenario 3D. Por eso es importante tener
presente que cualquier dibujo, boceto, esquema... no es evidente por sí
mismo, necesita ser interpretado (la animación anterior del teorema de
Pitágoras es un excelente ejemplo del significado oculto tras una imagen).
Dandelin.ggb
La combinación de las vistas 2D y 3D nos proporciona más oportunidades para
aprovechar la estética subyacente a muchas construcciones matemáticas. En
este ejemplo aparecen las esferas de Dandelin.
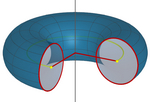
teoremas del centroide de Pappus-Guldin.ggb
Los teoremas de Pappus-Guldin facilitan el cálculo de áreas y volúmenes de
cuerpos de revolución (siempre que la recta o curva generatriz no corte al
eje de rotación). Inversamente, también se pueden emplear estos dos teoremas para determinar la posición del
centroide (o baricentro) de una curva o superficie plana (como en el caso de
la semicircunferencia y el semicírculo).
1. El área de una superficie de revolución es igual al producto de la longitud de
la curva generatriz por la distancia recorrida por el centroide
de esa curva al generar la superficie.
2. El volumen de un cuerpo de revolución es igual al producto del área de
la superficie generatriz por la distancia recorrida por el centroide de esa
superficie al generar el cuerpo.
 cortes
del hipercubo.ggb
Incluso podemos representar los cortes de un hipercubo (en este ejemplo, las
secciones poliédricas son perpendiculares a la diagonal principal del
hipercubo).
 criba
de Eratóstenes.ggb
La vista 3D también puede ayudar a visualizar algunas distribuciones. En
este ejemplo, podemos observar como la disponer los números naturales en una
estructura cilíndrica, todos los múltiplos de un número primo quedan
atrapados en la misma espiral.
cuadrados mágicos impares en el toro.ggb
Construir un cuadrado mágico de un
número impar (n) de filas es muy fácil siguiendo el siguiente procedimiento:
primero, colocamos el número 1 en el centro de la primera columna.
Después, los siguientes números consecutivos (2, 3... hasta n2), se colocan
en el elemento de la tabla situado justo abajo y a la izquierda del
anterior, es decir, en la fila siguiente y la columna anterior. Si no se
puede porque:
a) No hay fila siguiente. En este caso, se toma la primera fila.
b) No hay columna anterior. En este caso, se toma la última columna.
c) La posición indicada ya ha sido ocupada anteriormente. En este caso, el
siguiente número se coloca en la posición justo a la derecha del último
colocado y se prosigue el procedimiento mencionado.
Los dos primeros pasos del procedimiento anterior nos hacen saltar abruptamente
de la primera a la última columna y de la última a la primera fila. Sin
embargo, imaginando que la parte superior de la tabla estuviera pegada a
la parte inferior y que la parte izquierda estuviera pegada a la parte
derecha, la columna anterior a la primera sería la última y la fila
siguiente a la última sería la primera.
Así, en el toro, las líneas diagonales que antes eran discontinuas se
transforman en líneas continuas.
Representaciones de la realidad
GeoGebra permite la representación gráfica de la estructura y el
comportamiento de muchos objetos, mecanismos y situaciones reales. He aquí
algunos ejemplos.
Funcionamiento de máquinas
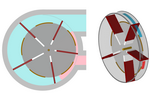
compresor de aire
de paletas.ggb
El dinamismo de GeoGebra puede ser usado para modelizar el funcionamiento de
diversos mecanismos y aparatos. En este ejemplo visualizamos el esquema de
un compresor de paletas. El aire entra por la parte superior y las paletas
lo arrastran hacia la parte inferior. Como el disco interior está
descentrado, el aire queda comprimido antes de salir con fuerza. Obsérvese
el movimiento centrífugo, debido al giro, de las paletas. (También se puede
ver esta
versión 3D, pero, por algún motivo, actualmente resulta inestable.)
Estructura de las conchas
Las superficies se pueden parametrizar y también se
pueden crear familias de superficies cuyas formas varían al
variar los parámetros que las definen.
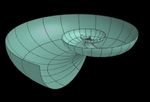
conchas.ggb
Un caso espectacular es el de las conchas, que sigue un
patrón de crecimiento definido por la autosemejanza. Los moluscos que
crean estos caparazones deben ampliarlos según van
creciendo. En muchos casos, esto significa sellar el
habitáculo anterior cuando la nueva cámara ya esté lista
para residir en ella. Como todas las cámaras varían de
tamaño pero conservan la forma, se produce una estructura
espiral con patrón autosemejante que se puede modelizar.
Nota: a pesar de la aparente dificultad, esta construcción resulta sencilla debido a que se reducen las fórmulas a una lista
de parámetros dados. La parametrización parte del artículo Modells for mollusc shell shape
 de M.B. Cortie (1989).
La Tierra y el Sol
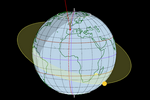
Tierra y Sol.ggb
Complementariamente a la realización de construcciones sencillas, resulta
muy interesante intentar destripar escenarios complejos, analizando cada parte y
su funcionamiento. En esta, podemos distinguir la incorporación del tiempo
real UTC (hora, día, mes, año), la latitud y longitud, el movimiento
aparente del Sol, el ángulo que forma la eclíptica respecto al ecuador,
los trópicos y los círculos polares, la causa de las estaciones, los
equinoccios y solsticios, el Punto Aries, la ascensión recta y la
declinación, el orto y el ocaso, y la analema del sol, entre otros
conceptos.
Conmutatividad de los epiciclos
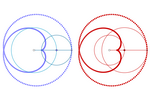
conmutatividad.ggb
En las tres construcciones siguientes aparecerán epiciclos. Antes
de verlas, resulta conveniente tener presente lo siguiente:
Debido a la conmutatividad de la suma vectorial, el lugar geométrico
generado por un punto en un epiciclo no se altera si intercambiamos el
deferente (1ª circunferencia) y el epiciclo (2ª
circunferencia), o si intercambiamos epiciclos sucesivos. Esto significa
que podemos ordenar los epiciclos por radios ascendentes sin que esto
afecte al resultado final.
La cuerda vibrante
vibración punto
medio cuerda.ggb
La historia del problema de la cuerda vibrante, que implicó a algunos de
los mejores matemáticos del siglo XVIII y principios del XIX (Taylor,
d'Alembert, Daniel Bernouilli, Euler, Fourier, Lagrange, Laplace, Abel y
Dirichlet, entre otros) en una discusión tan vibrante como la cuerda.
Finalmente, se concluyó que la vibración de la cuerda es el resultado de
una suma (serie convergente de Fourier) de movimientos sinusoidales
(armónicos). En esta construcción, además del movimiento de la cuerda,
podemos apreciar como su punto medio es insensible a los armónicos pares
(ya que no vibra en ellos). El movimiento de este punto medio lo
podemos visualizar también como resultado de una serie de epiciclos.
Versatilidad de los epiciclos
versatilidad.ggb
En realidad, cualquier trayectoria puede ser
representada con un número (tal vez infinito) de epiciclos, ya que estos pueden ser representados como series de Fourier;
en este ejemplo, podemos ver como con 39 epiciclos podemos aproximar la
forma de un objeto muy asociado a Jerez. Gracias a la conmutatividad de
los epiciclos, podríamos (aquí no lo hemos hecho) disponer los círculos
en orden ascendente de sus radios.
Flor de Venus
flor de Venus.ggb
Cada 8 años,
Venus da casi exactamente 13 vueltas alrededor del Sol. En ese tiempo,
Venus adelanta 5 veces a la Tierra, generando una cáustica
que recuerda a 5 cardioides entrelazadas (sería una cardioide si el año terrestre durase
el doble que el venusiano).
 Más
precisamente, la fracción de los períodos orbitales entre ambos
planetas (365,256/224,701) está muy próxima a ser 13/8 (1+5/8). Por
tanto, el ciclo relativo se repite cada 8/5=1,6 años, que equivale a
576º (una vuelta y 216º) de vueltas terrestres, lo que provoca la
aparición de ese patrón pentagonal conocido como pentagrama o flor de Venus.
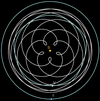 Como las trayectorias de Venus y la Tierra son casi
circunferencias, obtenemos el mismo diagrama sustituyendo el
segmento Tierra-Venus por su punto medio PM.
También obtenemos el mismo diagrama como un epiciclo de Venus visto
desde la Tierra, sin más que ajustar la escala de las distancias a la
mitad. Esto se debe a que si
sumamos la mitad del vector Sol-Tierra con la mitad del vector Sol-Venus,
obtenemos precisamente el vector Sol-PM.
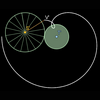
Suponiendo que las trayectorias de Venus y la Tierra fueran
circunferencias perfectas y la relación 13/8 fuera exacta, la flor de
Venus sería una epitrocoide perfecta, es decir, podría ser generada por
una gigantesca rueda que rodase (sin deslizamiento) sobre un círculo
centrado en la Tierra con radio 5/13 de la distancia de la Tierra al
Sol.
Notas:
  1. La
flor de Venus se puede materializar fácilmente mediante hilos tensados (hiloramas).
Es muy conocido por los aficionados a la astrología y otras pseudociencias, de modo que se
pueden encontrar su diseño en todo tipo de objetos, como en joyería.
2. La imagen del diagrama que aparece en la construcción proviene de la entrada
"epiciclo" en Wikipedia - Movimiento aparente (J. Ferguson 1710-1776
basado en un diagrama similar de G. Cassini 1625-1712).
3. La construcción ha sido realizada con los datos reales de la Tierra y
Venus, pero se puede simplificar mucho usando circunferencias en vez de
elipses, sin que se aprecie diferencia alguna dada su pequeña
excentricidad. También se puede usar directamente la relación 13/8.
4. Más
adelante, en la sección Autómatas, se puede ver otro ejemplo de modelización de
la realidad física (órbitas elípticas.ggb).
La súper hoja de cálculo: billares dinámicos
La hoja de cálculo de GeoGebra no solo permite expresiones numéricas, textos
y fórmulas, sino que además admite cualquier objeto de GeoGebra: puntos,
rectas, curvas, funciones, listas, etc.
Como ejemplo, veremos su uso sistemático para el análisis del comportamiento
de billares con diferentes formas. Considerar al billar como objeto de
estudio puede que parezca algo frívolo, pero en realidad tiene mucha
importancia en la física práctica; por ejemplo, en un horno microondas se
intenta que los rebotes en las paredes calienten el plato del modo más
uniforme posible, mientras que un cable de fibra óptica se intenta que los
rebotes del láser no provoquen interferencias. Además, los billares
dinámicos sirven de modelo para importantes problemas en el estudio del caos cuántico.
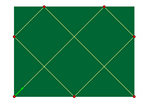
Orden. Billar rectangular con dimensiones enteras
billar rectangular.ggb
En un billar rectangular de dimensiones enteras (es decir, como no se
especifica la unidad, basta que su cociente sea racional), podemos plantear
un bonito problema:
¿Cuántos rebotes dará una bola enviada con un ángulo de 45° desde una
esquina antes de alcanzar otra esquina?
Orden. Billar cuadrado
billar cuadrado.ggb
La regularidad de las trayectorias resulta todavía más patente en un billar
cuadrado. De hecho, podemos calcular fácilmente dónde se encontrará la bola
al cabo de cualquier número de rebotes en las bandas.
En un billar normal, la bola rebota en la banda simétricamente respecto a su
perpendicular en el punto de contacto.
Orden. Billar circular
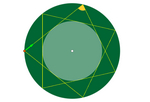
billar circular.ggb
Si la banda es curva, en vez de recta, el eje de simetría es la
perpendicular a la recta tangente a la curva en ese punto. En el caso de un
billar circular, esa perpendicular es siempre el radio del círculo.
En el billar circular, todos los segmentos entre dos rebotes consecutivos
tienen la misma longitud. Dependiendo del ángulo de salida, podemos
determinar con facilidad el radio del círculo interior que quedará inscrito
en la trayectoria poligonal. También podemos encontrar cómo han de ser los
ángulos para que la trayectoria se cierre.
Además, en la construcción se usa un guion de GeoGebra para simular el
movimiento de la bola.
No trivial. Problema de Alhacén
problema de Alhacén.ggb
La construcción anterior nos recuerda el problema de Alhacén:
¿Hacia qué punto hay que lanzar una bola en un billar circular para
alcanzar a otra después de rebotar en la banda?
Este enunciado es equivalente al siguiente: Dada una fuente de luz y un
espejo esférico, encontrar el punto del espejo donde la luz se verá
reflejada para el ojo de un observador dado.
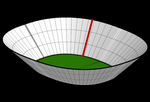
Orden. Billar elíptico
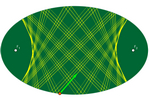
billar elíptico.ggb
El billar elíptico resulta más entretenido... y complicado. Si apuntamos a
un foco, la trayectoria irá de foco a foco. Si apuntamos entre los focos, la
trayectoria será tangente a un hipérbola (cáustica). En otro caso, la
trayectoria ser la cáustica de otra elipse. En este ejemplo se pueden
apreciar, además, diversas trayectorias periódicas, tanto cerradas como
abiertas.
(Al igual que en el billar circular, hemos incluido en la construcción un
guion de GeoGebra para simular el movimiento de la bola.)
Caos. Billar de Sinái
 billar
de Sinái.ggb
Los
arcos en los bordes pueden ser neutros (como en el billar cuadrado o
rectangular), focalizadores (como en el billar circular o elíptico) o
dispersores, según concentren o dispersen las trayectorias.
En el billar de Sinái aparece el caos determinístico debido a los arcos
dispersores convexos de su agujero interior.
Caos. Estadio de Bunimóvich
billar de Bunimóvich.ggb
Este billar es un rectángulo limitado por semicírculos en dos lados
opuestos. Antes de Bunimóvich se creía que para poder dispersar la
trayectoria era imprescindible contar con dispersores convexos (como en el
billar de Sinái). Sin embargo, el estadio de Bunimóvich se comporta como un
dispersor, siempre que la trayectoria pase entre el borde circular cóncavo y
el centro del correspondiente círculo.
Toro: loxodrómicas y circunferencias de Villarceau
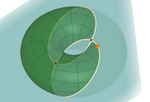
toro y Villarceau.ggb
El toro no tiene bordes, así que cualquier bola se moverá siguiendo siempre
el mismo rumbo α
(línea loxodrómica). Si el radio exterior es R y el interior es r (con r<R),
esta trayectoria se cierra cuando la expresión tan(α) sqrt(R2-r2)/r sea
un número racional.
En el caso particular de que ese cociente sea 1 (es decir, sen(α)=r/R),
se forman las circunferencias de Villarceau.
Caos. Toro con agujero
billar toro con agujero.ggb
Para generar el caos, basta hacer un agujero en el toro. El borde creado se
comporta entonces como un dispersor convexo, de forma similar al billar de
Sinái.
Caos. Curva cerrada arbitraria
billar curvo.ggb
Desgraciadamente, a día de hoy (ver
forum
), la representación del billar arbitrariamente curvo (donde el
borde es un spline) presenta problemas porque a veces GeoGebra es incapaz
de encontrar todos los puntos de corte del spline con algunas rectas.
Sistemas dinámicos
Existe una gran diferencia entre condición y cálculo. Por ejemplo, la
condición para que un número real sea raíz de una función es que el valor
numérico de la función, para ese número, sea cero. Calcular esa raíz es otro
cantar.
Habitualmente los cálculos exigen procedimientos cuyo aprendizaje es largo y
tedioso. Pero que no sepamos realizar esos cálculos no es impedimento para
apropiarnos de la idea matemática que abordan. Estas ideas pueden parecer
mucho más atractivas si sacrificamos algo de cálculo... o lo simplemente lo
posponemos a un nivel más avanzado.
Puntos cargados
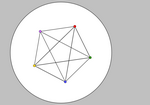
círculo con puntos.ggb
Crearemos un sistema dinámico que se estabilice por sí mismo:
Pongamos dos puntos en el interior de un círculo. Imaginemos que tanto los
puntos como el borde del círculo están cargados eléctricamente, con la misma
carga.
Los dos puntos se repelen entre sí, y son repelidos por la circunferencia,
con intensidad inversamente proporcional al cuadrado de la distancia. Inmediatamente, buscarán el equilibrio,
que se alcanzará cuando los dos puntos se dispongan simétricamente respecto
al centro del círculo y a una distancia entre sí igual a un tercio del diámetro.
 círculo
con 10 puntos.ggb
Si añadimos más puntos, el equilibrio dará lugar a polígonos regulares, como
cabría esperar. Aquí vemos cómo 10 puntos se equilibran formando el decágono
regular (dependiendo de las condiciones iniciales, podría formarse también
un eneágono con su centro).
 cuadrado
con 5 puntos.ggb
No
siempre resulta tan intuitivo predecir cuál serán las posiciones estables. En este caso, cinco puntos en un cuadrado encuentran,
además de la distribución que cabría esperar, otras cuatro posibles
distribuciones, simétricas entre sí.
robot sensible.ggb
Incluso pueden observarse situaciones en las que una levísima diferencia en
las condiciones iniciales diferencie el orden del caos. En este ejemplo, los
puntos se repelen entre ellos igual que antes, pero ahora además son
atraídos, con doble intensidad, al origen de coordenadas.
Robot entre enemigos
 robot_entre_enemigos.ggb
Ahora crearemos un sistema dinámico jugando con la atracción y la
repulsión.
El robot (punto rojo P) conoce la
posición final que desea alcanzar (punto verde O) pero debe esquivar
una serie de enemigos (puntos azules).
Una vez colocados los puntos, llamamos atractor al vector unitario
de P a O.
Como antes, creamos
los vectores unitarios que van desde cada punto azul hasta P y los dividimos
por el cuadrado de la distancia que los separa. Estos vectores serán las repulsiones que alejarán a P
cuando esté demasiado cerca de ellos. Ahora sumamos todos estos vectores
para obtener el vector avanza.
-
Creamos un
deslizador t que va a servirnos para animar el punto P (al que hemos
activado el rastro), de forma que varíe con bastante frecuencia, por
ejemplo, entre 0 y 1 con paso 0.01.
-
Finalmente,
creamos la constante inc = 0.2, que nos servirá para establecer el
avance en cada paso.
Ahora escribimos
el programa de nuestro robot. Cada vez que se actualice el valor de t, se
ejecutará el siguiente guion con una única instrucción:
Valor(P, P + inc
avanza)
Ya solo nos
queda animar el deslizador t.
Nota: Si queremos volver a repetir el experimento, basta con borrar el
rastro (Ctrl-F) y recolocar los puntos a nuestro antojo.
Modelizando la realidad física: Órbitas elípticas
órbitas elípticas.ggb
Colocamos el punto S (Sol) en el centro de coordenadas y un punto T (Tierra)
con velocidad inicial el vector v. Si d es la distancia TS y k es una
constante, tenemos el vector de fuerza gravitatoria:
g = k / d²
VectorUnitario(Vector(T, S))
Ahora solo hay que introducir un deslizador auxiliar para que, cada vez que
se actualice, ejecute el simplísimo guion:
Valor(T, T + 0.02 v)
Valor(v, v + 0.02 g)
¡Y ya tenemos el movimiento elíptico! (Obsérvese que no hemos empleado
ninguna ecuación ni lugar geométrico.)
Nota: Esta construcción fue realizada en colaboración con mi
compañero de departamento Julio Valbuena Herrero, quien adaptó la idea
expuesta por
Richard Feynman en su famoso libro The Feynman Lectures on Physics (1963,
volumen I
,
9-7, Planetary motions).
Autómatas
Exploraciones dinámicas
Hasta ahora, el comportamiento de los robots quedaba determinado por
vectores definidos a partir de los otros puntos. En este último apartado,
crearemos robots que antes de emprender un movimiento
husmeen qué sucede a su alrededor y, basándose en los valores obtenidos,
tomen una decisión.
 robot
recíproco Pitágoras.ggb
En este ejemplo, queremos demostrar de modo dinámico y automático el recíproco del teorema de Pitágoras.
Llamamos dif la expresión
abs(a²+b²-c²). Objetivo: dif = 0.
-
Creamos un
deslizador t que va a servirnos para animar el vértice C (al que
hemos activado el rastro), de forma que varíe con bastante frecuencia.
-
Otro deslizador
inc para establecer el avance en cada paso.
-
Finalmente,
creamos dos objetos auxiliares: C0 y dif0 que valdrán
para mantener, respectivamente, los valores actuales de C y dif.
Ahora escribimos
el programa de nuestro robot. Cada vez que se actualice el valor de t, se
ejecutará el este guion de instrucciones (el símbolo # sirve
para añadir comentarios). Solo queda animar el deslizador t.
Nota: Si queremos volver a repetir el experimento, debemos recordar
devolver inc al valor 0.1.
 robot punto
Fermat.ggb
En este otro ejemplo, queremos encontrar el punto de Fermat de un
triángulo dado. Para ello, hemos sustituido el papel del vértice C del
triángulo y de su alter ego C0 por un punto exterior al triángulo: F
y F0.
Ahora, el objetivo es minimizar la expresión dif = abs(F-A) +
abs(F-B) + abs(F-C).
En este caso, el mensaje de “proceso terminado” aparecerá cuando el
incremento sea indistinguible de 0 (sin usar el CAS de GeoGebra, es
decir, del orden de una cien millonésima).
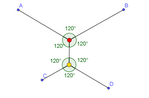 robot puntos
Steiner.ggb
Si generalizamos el punto de Fermat a más vértices, obtenemos el árbol
de Steiner (añadiendo los puntos de Steiner que sean necesarios).
Observemos que los robots no saben dónde están los puntos A, B, C
y D, basta con que sepan a qué distancia están en cada instante.
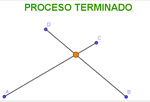
robot mediana geométrica cuatro puntos.ggb
Los puntos de Steiner minimizan la longitud del árbol que conecta los
cuatro puntos dados, pero a costa de añadir más de un vértice. Ahora
nuestro deseo es encontrar el punto que minimiza la suma de las
distancias desde él a los puntos dados (mediana geométrica).
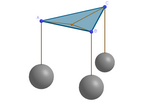
robot
mediana geométrica ponderada.ggb
En este otra generalización del punto de Fermat, los vértices del
triángulo no pesan lo mismo, es decir, cada distancia se pondera en
función de esos pesos.
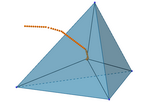
robot
mediana geométrica tetraedro.ggb
Esta última generalización del punto de Fermat sustituye el triángulo
por su versión espacial, el tetraedro.
Problemas de optimización
robot problema
nadador.ggb
Como vemos, cualquier problema de optimización del valor de una función
objetivo se puede representar dinámicamente siempre que sepamos expresar
analíticamente esa función objetivo. En este conocido "problema del
nadador", se trata de minimizar el tiempo total para ir nadando del
punto P a la orilla y después correr la distancia que falta para llegar
a Q.
Secuencias de acciones
torres de Hanoi.ggb
Como podemos asociar un guion a un deslizador, la simple animación
de este nos permite reproducir una secuencia de acciones tantas veces
como deseemos. En este ejemplo, lo usamos para resolver automáticamente
el rompecabezas de las torres de Hanoi.
 laberinto.ggb
En este último ejemplo, el robot ha de adaptarse al entorno: no tiene ninguna información sobre
la forma del laberinto. Solo detecta si hay espacio libre a su
derecha (en cuyo caso gira a la derecha para pegarse a la pared derecha)
o si hay un obstáculo enfrente (en cuyo caso gira a la izquierda).
Esta sencilla norma basta para pegarse de su pared derecha y
conseguir salir del laberinto (aunque no lo haga en el menor recorrido
posible). Para ello, bastan dos instrucciones en el guion del robot:
# Si la distancia a la pared derecha es mayor que
0.4 unidades, gira a la derecha; si no es así, pero la distancia a la pared de
enfrente es menor que 0.15, gira a la izquierda; en cualquier otro caso,
continúa recto.
Valor(v, Si(dPD>0.4, vn, Si(dPA<0.15, -vn, v)))
Valor(P, P + v)
|
