|
GeoGebra, o explorador matemático
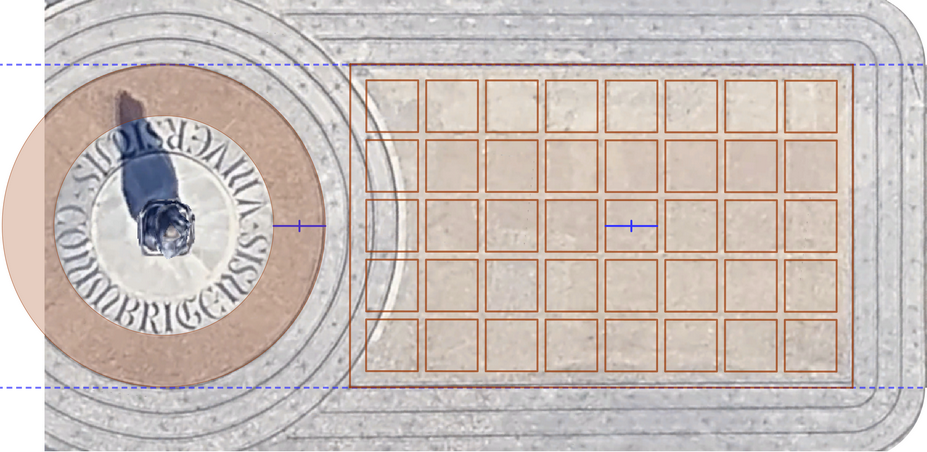
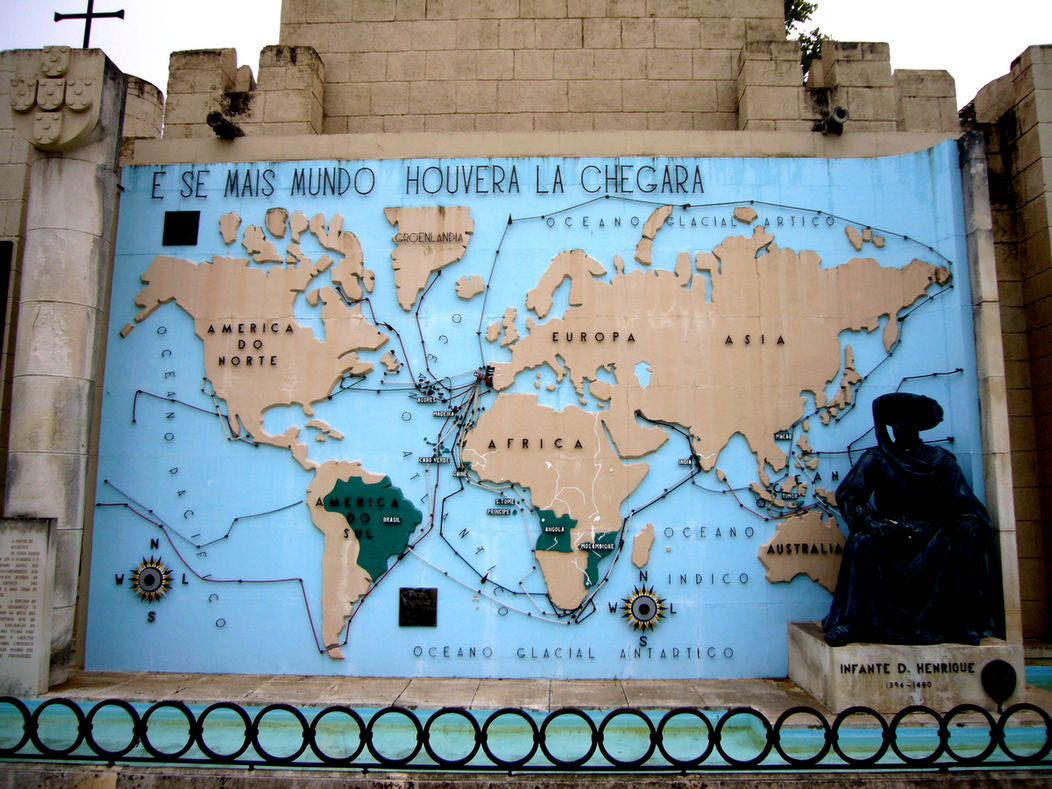
Vista zenital da Estátua de Dom Dinis, com a inscrição UNIVERSITATIS COIMBRIGENSIS
rafael.losada@gmail.com II Congresso Internacional GeoGebra Universidade de Coimbra 23-25 Outubro 2025
Traço humano
O cabeçalho desta página é uma
vista aérea da estátua de Dom Dinis, situada mesmo em frente a este
Departamento de Matemática da Universidade de Coimbra. Como o GeoGebra permite
inserir imagens como fundo da vista gráfica, podemos destacar os elementos que
quisermos e fazer anotações sobre eles. Imagens como esta são muito fáceis de
obter e permitem levantar uma série de questões conforme o nível desejado, desde
"Quantos quadrados aparecem?" ou "Consegues calcular quantos são sem os contar
um a um?", até "Tomando como unidade de superfície a área de cada quadrado, qual
é a área da coroa circular colorida?" ou "Qual é a área da parte visível do
retângulo (repara que os círculos que rodeiam a estátua invadem parte dele)?".
As ferramentas do GeoGebra ajudam os alunos a explorar, calcular e verificar as
suas conjeturas.
Google Maps @40.2036376,-8.5959846,1252m
Estamos na Universidade de Coimbra (UC), Património Mundial desde 2013. Os nomes de algumas ruas refletem a profunda influência da Universidade nesta "cidade dos estudantes". A menos de 400 metros daqui, podemos caminhar pela Rua da Matemática, pela Travessa da Matemática e pelo Largo da Matemática.
Há mais de um século, os estudantes universitários fundaram numerosas Repúblicas (comunidades de estudantes, cerca de 10 ou 20, que compartilham moradia, refeições, despesas, passeios, festas e até bandeira). Nas imagens, três dessas repúblicas estudantis, situadas nos números 2, 6 e 40 da Rua da Matemática (em homenagem a André do Avelar, que ali viveu).
Outros matemáticos históricos da UC foram Pedro Nunes, José Anastácio da Cunha, Miguel Franzini, Florêncio Mago Barreto Feio e Rodrigo Ribeiro de Sousa Pinto, que dá nome ao bairro que fica mesmo ao lado das Escadas Monumentais que descem de onde estamos:
O Dia Internacional da Matemática (Dia do Pi, 14 de março) de 2025 foi dedicado à criatividade comum presente tanto na Arte quanto na Matemática. Não surpreende, portanto, que ao longo da história a arte tenha recorrido frequentemente à matemática em sua busca por métodos de construção para representar a realidade, como o estudo da perspectiva, ou expressar a beleza, por meio de propriedades como proporcionalidade e simetria.
Não é difícil encontrar exemplos dessa relação ao nosso redor. A menos de 400 metros de onde estamos, encontra-se o claustro da Sé Velha (século XIII), no qual podemos apreciar 20 rosáceas, todas diferentes (fotos de Mariló Fernández Mira, 2007). Cada uma das quatro faces do claustro tem cinco arcos quebrados, e cada um deles contém uma rosácea e dois arcos de volta perfeita. Nos cantos, os arcos ogivais se cruzam na altura dos arcos de volta perfeita, produzindo um efeito curioso.
Recoloquei as rosáceas sobre os mesmos dois arcos de fundo, para mostrar suas diferenças e simetrias (ignorando um pequeno dano que, curiosa ou deliberadamente, embora quebre a simetria rotacional, preserva a simetria diedral). Essas rosáceas têm desenhos simples, sendo assim possíveis de serem reconstruídas com GeoGebra no ensino secundário. As 20 rosáceas diédras têm ordens 3, 4, 5, 6 e 8, que correspondem a polígonos construíveis, enquanto 7 não é (Ortega, Ortega, Ortega e Crespo, 2005). Este mesmo claustro também pode ser usado para propor a construção dos arcos ogivais e de volta perfeita (Arranz, Losada, Mora e Sada, 2008 e 2009).
Certamente, a primeira ideia que lhe vem à cabeça para utilizar o traço ativado é desenhar, transformá-lo num lápis. Por exemplo, o uso do traço com cor facilita a criação e visualização de qualquer rosácea, sejam cíclica ou diédrica (Losada, 2010).
Vamos agora ao Museu Nacional Machado de Castro, a menos de 300 metros daqui.
Nele são preservados catorze azulejos matemáticos do século XVIII que decoravam algumas salas de aula do antigo colégio jesuíta. Como descobriu, nos anos 90, António Leal Duarte (do Departamento de Matemática em que nos encontramos), esses azulejos reproduzem algumas figuras de uma edição de os Elementos de Euclides (Tacquet, 1683), como aparece à direita desta imagem (Requena, 2014).
Essa figura corresponde à Proposição XVII do Livro III, onde se fornecem e demonstram instruções para traçar uma tangente a uma circunferência a partir de um ponto sobre ela ou sobre o seu exterior.
Antes de apresentar mais exemplos do uso do traço, lembremos que com o GeoGebra é muito fácil realizar inversões em uma circunferência.
Aqui vemos como podemos criar facilmente, por inversão 2D, uma corrente de Steiner, verificando se a inversão mantém as tangências, mas os centros dos círculos já não formam uma circunferência, mas sim uma elipse (verde).
Ao transferi-la para 3D, a envolvente das esferas que se invertem (na esfera azul turquesa) forma um toro. A inversão desse toro nessa mesma esfera, ou seja, a envolvente das esferas invertidas correspondentes, forma um cíclideo de Dupin (no caso de 6 esferas, o ciclídeo envolve o sexteto de Soddy). Com infinitas esferas, obtemos a corrente de Papo, onde o ciclídeo de Dupin corresponde à inversão de um cilindro.
Os azulejos geométricos mais comuns não são do tipo matemático que vimos, mas sim aqueles projetados para repetir um padrão por meio de teselação periódica. Embora a influência islâmica desse tipo de arte seja maior na Espanha do que em Portugal, onde os azulejos mais comuns têm caráter mais figurativo que geométrico, não faltam exemplos.
Podemos encontrar azulejos geométricos na Sé Velha de Coimbra, mas escolhi este azulejo do Palácio Nacional de Sintra pelo seu desenho simples e pela harmonia das duas cores predominantes, o que aumenta o efeito de contraste. Essa complementaridade se traduz em uma complementaridade numérica nos canais RGB (a mistura aditiva das duas cores resulta em branco).
Se tirarmos uma foto do azulejo (ou qualquer região retangular capaz de teselar por translação) e a colocarmos como imagem de enchimento de qualquer forma plana, como um círculo, mover a forma moverá a imagem pela tesselação. Assim, basta ativar o traço para o reproduzir. No entanto, esta tática, embora muito atrativa, só funciona para azulejos retangulares, não é muito eficaz para mudar de cor rapidamente e também não nos permite inverter o azulejo, como faremos.
A construção permite não só a translação do azulejo por todo o plano (usando a espiral de Ulam), com essas ou outras cores, mas também sua inversão. Para conseguir isso sem sobrecarregar o GeoGebra com a multiplicidade de objetos, em cada passo apenas um azulejo é transladado (seja uma vez invertido ou não), de modo que os azulejos que vão aparecendo não são novos objetos, mas o traço deixado por um único azulejo (Losada, 2025). Podemos também visualizar o mosaico em perspetiva, utilizando a visualização 3D.
Agora vamos nos
concentrar nos mosaicos regulares. Na geometria euclidiana, existem apenas
três: o triangular, o quadrado e o hexagonal. Usando a notação {p, q},
onde p é o número de lados do polígono regular e q é o
número de polígonos que cercam cada vértice, esses mosaicos são
expressos como {3, 6}, {4, 4} e {6, 3}.
Livro I. Postulado V dos Elementos de Euclides (reorganizado na edição de Oliver Byrne como Axioma XII)
Podemos diferenciar a geometria euclidiana das que não cumprem o quinto postulado de Euclides, a elíptica e a hiperbólica, usando configurações {p, q}, ou seja, polígonos regulares de p lados onde em cada vértice se encontram q. Em particular, o valor da expressão (p – 2)(q – 2) discrimina cada geometria. Quando é igual a 4, temos três casos possíveis (as tesselações regulares habituais). Quando é menor que 4, obtemos as cinco partições regulares da esfera, origem dos cinco sólidos platônicos.
Nota: nesta classificação supomos que os polígonos da tesselação regular têm pelo menos 3 lados. Na geometria elíptica podem ocorrer tesselações com polígonos de 2 lados (ou até apenas 1!).
As retas da geometria euclidiana tornam-se circunferências máximas na esfera (como duas dessas circunferências sempre se intersectam, não existem paralelas, e portanto o postulado das paralelas não se cumpre).
Para obter as cinco partições da esfera, transformamos as arestas dos poliedros em arcos de círculos máximos. Usando esse mesmo procedimento, podemos transformar qualquer mosaico plano (geometria euclidiana) em um mosaico esférico (geometria elíptica). Se tiver uma impressora 3D, estes mosaicos podem ser utilizados como luminárias personalizadas 🙂.
Para colorir cada polígono esférico recorremos às funções arg() e alt(), com as quais um polígono (plano) pode ser facilmente transformado numa superfície esférica, cujo rasto de cor variável cobrirá toda a esfera. Mas criar cada polígono esférico requer muitos recursos, por isso, para o nosso mosaico, optamos por criar pequenos arcos de círculos, com o traço ativado, em vez de superfícies (Losada, 2025).
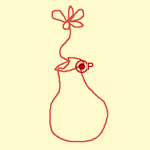
Que acontece quando (p – 2)(q – 2) é maior que 4? Com o GeoGebra, podemos descobrir. Assim como na geometria elíptica o tamanho de cada polígono regular é determinado pela esfera, agora será determinado pelo círculo unitário (lembremos que na geometria euclidiana o polígono é escalável, podendo ter qualquer tamanho).
No disco de Poincaré, as retas da geometria euclidiana tornam-se arcos de circunferências ortogonais à circunferência unidade (de modo que, por um ponto exterior a um deles, pode-se traçar mais de um que não o intersete, e portanto o postulado das paralelas não se cumpre).
A construção não utiliza nenhuma ferramenta de geometria hiperbólica; apenas aplica repetidamente o comando de inversão em certas circunferências. Tal como antes, graças ao traço deixado por cada célula, basta atualizar uma célula (refletindo-a na seguinte), de modo que o GeoGebra mantém em todo momento a sua capacidade de cálculo e execução. Para isso, basta adaptar à geometria hiperbólica a espiral de Ulam usada na construção euclidiana, obtendo discos de Poincaré (Losada, 2025) ideais como bases para copos 🙂.
Assim, podemos ver as cadeias de Steiner que se geram, criar o nosso próprio teselado com a peça que quisermos, gerar o disco com o grupo triangular que Coxeter enviou ao seu amigo Escher, a resposta deste na forma da gravura Circle Limit I, a autodualidade e, de um modo geral, gerar qualquer teselado hiperbólico regular {p, q}. O número cromático (nc) não depende da geometria (pois o grafo dual é um conceito topológico), mas apenas dos valores {p, q}. Quando q é par, nc = 2. Quando q = 3 e p é ímpar, forma-se uma roda com um número par de vértices (Wp+1), pelo que nc = 4. Nos restantes casos, nc = 3.
Seguramente, estas são as primeiras tesselações 'completas' no disco de Poincaré realizadas com o GeoGebra e, muito provavelmente, este é o primeiro mosaico hiperbólico feito com um azulejo com influência mudéjar encontrado em Portugal 🙂. Agora, para realizar qualquer outro procedimento semelhante, basta alterar o conteúdo das listas que definem o tile central, sendo que as suas reflexões subsequentes serão realizadas automaticamente.
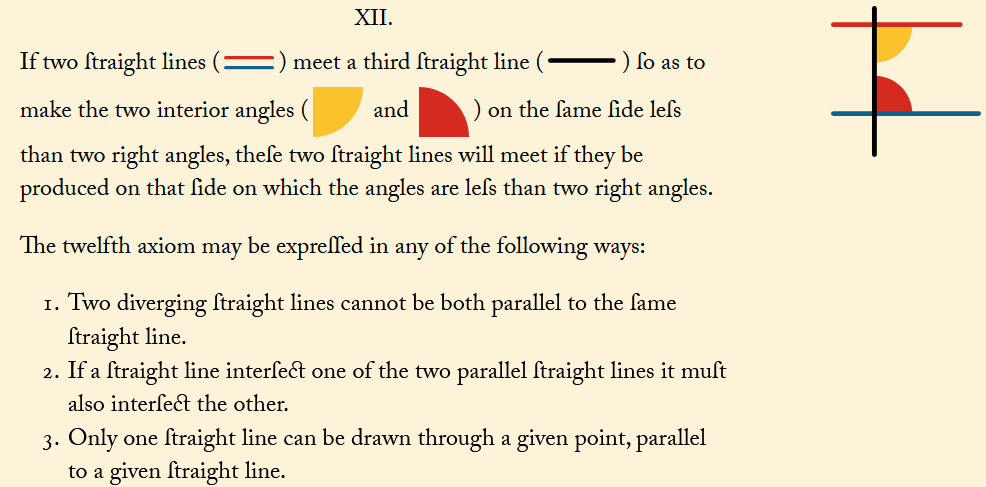
A construção do azulejo fundamental costuma ser uma atividade bastante instrutiva. Neste exemplo, mostramos como criar, a partir de um tetraedro, um azulejo que tesela o plano por translação. Cortamos o tetraedro seguindo um caminho hamiltoniano, ou seja, passando a tesoura ou o estilete apenas uma vez por seus quatro vértices.
Depois, desenvolvemos o tetraedro. Está demonstrado que a figura resultante sempre tesela o plano (Akiyama & Matsunaga, 2015).
Podemos usar listas vazias como repositórios para armazenar dados. Neste caso, usaremos a lista "reg", que armazena os dados das posições de um ponto móvel para substituir seu traço por uma poligonal que une todas essas posições. Cada vez que o ponto P muda de posição, executa-se a instrução DefinirValor(reg, Juntar(P, reg)).
A vantagem desse método é que ele melhora a visualização do trajeto percorrido e também permite estimar seu comprimento.
Podemos atribuir um script a um seletor
animado, de modo que, sempre que o seu valor for atualizado, ele execute as
instruções do GeoGebra nele contidas. Esse procedimento, juntamente com o traço
ativado, permite visualizar o percurso dos pontos que seguem essas instruções.
O ponto laranja representa o Sol, o azul, a Terra, e o branco, Vénus. A cada 8
anos, Vénus dá quase exatamente 13 voltas ao redor do Sol. Nesse tempo, Vénus
ultrapassa a Terra 5 vezes, gerando uma envolvente que lembra 5 cardioides
entrelaçados (seria um
cardioide se o ano terrestre durasse o dobro do ano
venusiano).
O GeoGebra permite criar o diagrama de Voronoi. Embora apenas trace o diagrama, é possível colorir as regiões recolhendo posteriormente as informações fornecidas pelo grafo. Nesta construção, é possível observar as diferentes regiões, bem como a triangulação de Delaunay e o fecho convexo de até 50 sítios.
Contudo, há situações em que o comando Voronoi comete erros. Além disso, presume que a distância utilizada seja a distância euclidiana (L2). Graças ao traço de cor, podemos verificar o diagrama correto e criar outros baseados em diferentes métricas. Neste exemplo, usamos a distância táxi (L1) e a distância tabuleiro de xadrez (L∞), ambas associadas a circunferências quadradas. Este é o procedimento:
1. Criamos um seletor r de 0 até d, com d suficientemente grande (por
exemplo, a maior distância entre os sítios).
Dessa forma, à medida que cada circunferência reduz seu tamanho, seu traço afetará cada pixel, que ficará com a cor da última circunferência que o alcançar. Esta será a que tem o centro (que é um sítio) mais próximo daquele pixel (Losada, 2010).
Até o século XVIII, a matemática não estava preparada para enfrentar o
intrigante problema de determinar o movimento de uma corda esticada ao ser
tangida — um problema que daria origem ao que hoje se chama
Análise Harmônica.
Traço de cor dinâmica
Hipérboles cortando os lados de um triângulo em partes proporcionais (ver Apêndice II)
Podemos combinar as propriedades de Traço e Cor Dinâmica para criar um dispositivo poderoso e versátil para explorar relações existentes (e possivelmente ocultas) entre objetos matemáticos.
Estamos acostumados a ver e interpretar mapas de calor como os que representam variações de altitude em topografia ou de pressão/temperatura na meteorologia. Nesta seção, veremos como criar um mapa de calor matemático com GeoGebra e algumas de suas aplicações.
Colocamos um ponto livre com traço ativado e definimos sua cor dinâmica em função da condição c que desejamos visualizar. Como cada canal RGB exige um valor entre 0 e 1, não usamos diretamente c como valor do canal, mas sim qualquer função h tal que h(c) ∈ [0,1].
A função h pode ser, por exemplo, h(c) = |cos(𝜋/2 c)|, ou h(c) = 1/(1+|c|). Se quisermos destacar mais os valores próximos de 1, podemos incluir um coeficiente k maior que 1: h(c) = 1/(1+k|c|). Aqui vamos utilizar a função exponencial h(c) = e-|c|.
Nota: Naturalmente, nesse último caso (que será o mais usado), a
base e pode ser substituída por outra, como 2, 3 ou 10. De qualquer forma, o
valor do canal será 1 apenas quando c = 0, e quanto menor for o valor absoluto
de c, mais próximo de 1 ele será. Podemos substituir o ponto com traço ativado por um pequeno quadrado. Isso é útil quando queremos manter a visualização dos eixos cartesianos ou de uma imagem de fundo, uma vez que um ponto não permite controlar a sua opacidade, mas um polígono permite.
Inspirado por António, em resposta criei o primeiro scanner dinâmico de cor, um único ponto que varria sistematicamente todo o ecrã (Losada, 2009). Demorou apenas quatro horas a completar a tarefa 🙂, mas quando eu voltei a ver, estive quase a sofrer da síndrome de Stendhal.
O traço com cor dinâmica é uma ferramenta poderosa para investigação. No entanto, o movimento manual do ponto que deixa o traço é desconfortável e impreciso. Com a ferramenta Seletor, podemos animar automaticamente esse ponto, para que percorra os pixels da tela. Usando a Folha de Cálculo (incorporada no GeoGebra em junho do 2009), podemos obter a mesma imagem (que pode fazer lembrar o efeito do anel de diamantes num eclipse solar total) em poucos segundos, pois a partir do ponto com traço é simples criar uma coluna ou matriz de pontos (ou quadradinhos) que o acompanham, criando um scanner de cor dinâmica (Losada, 2010).
Nota importante: Se desejar modificar a construção, recomenda-se apagar temporariamente as células das colunas B, C... da segunda linha em diante antes de fazer qualquer modificação que afete todas essas células, pois o GeoGebra pode travar com tantas alterações simultâneas. Após realizar as mudanças desejadas nas células da primeira linha, basta arrastar para baixo e reconstruir toda a tabela.
Vejamos um exemplo simples. Dado um quadrilátero de área 30, queremos adicionar um novo vértice de modo que inserido entre os outros quatro (mantendo a sua ordem) o pentágono resultante tenha área 40. Onde devemos posicionar esse novo vértice? Podemos tentar intersecções da grelha, mas isso só levará a encontrar um ponto válido.
Ao passar o scanner, observamos que qualquer ponto de um quadrilátero com lados paralelos ao original serve. Agora podemos perguntar aos nossos alunos: Por quê? E como se constrói esse novo quadrilátero?
Uma vantagem da utilização de mapas de calor é que os alunos não podem "fazer batota" procurando a construção no ficheiro, uma vez que o quadrilátero que estão a visualizar não foi construído, nem há qualquer pista para o construir.
Podemos formular, dessa forma, todo tipo de situações, desde as mais simples como a anterior, até as mais sofisticadas. Por exemplo, neste caso partimos de três pontos fixos dados e queremos visualizar o lugar dos pontos cuja distância ao mais distante é a soma das distâncias dos outros dois pontos. O resultado corresponde aos zeros de uma curva algébrica de grau 4.
Tanto este exemplo como os dois anteriores mostram loci que não podem ser obtidas com outras ferramentas geométricas, nem mesmo com o comando LugarGeométrico.
Se atribuirmos um número natural a cada pixel, podemos visualizar a distribuição de coleções de números naturais. Neste exemplo, ordenei os pixels seguindo a leitura ocidental, ou seja, da esquerda para a direita e de cima para baixo, de modo que o número 1 é o pixel no canto superior esquerdo.
Assim, no primeiro quarto de milhão de números naturais, vemos a diferença na distribuição entre potências sucessivas de 2 (17 números), os números de Fibonacci (26), o número de lados de polígonos construtíveis (166), números quadrados (500) e números primos (22044). O pequeno número dos três primeiros casos recorda-nos que, na sua essência, todos os três dependem de uma exponencial. No último caso, a imagem resultante pode ser utilizada como decoração para papel de embrulho 🙂.
Os Elementos, livro I, proposição
47: teorema de Pitágoras
Segundo a lenda, na porta da Academia de Platão estava gravado "Que não entre ninguém que ignore Geometria" (AΓΕΩΜEΤΡΗΤΟΣ ΜΗΔΕIΣ ΕIΣΊΤΩ). Podemos ver uma réplica desta frase na fachada do edifício em que nos encontramos.
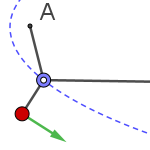
Na mesma fachada, à esquerda dessa frase, aparece a conhecida figura do "moinho" que representa o teorema de Pitágoras e, abaixo dela, uma demonstração baseada na proporcionalidade dos lados dos triângulos semelhantes (primeiro teorema de Tales) ou no teorema da altura. Os mapas de cor podem servir de introdução a resultados teóricos como este. Temos um triângulo de base BΓ e nos perguntamos onde devemos colocar o terceiro vértice A para que a soma das áreas dos quadrados azuis seja igual à área do quadrado vermelho.
Uma vez obtido o mapa, surgem as perguntas: por que aparece uma circunferência? Qual é seu diâmetro? Qual é a medida do ângulo subtendido por esse diâmetro em qualquer ponto da circunferência? Observamos que o mapa representa tanto o teorema de Pitágoras quanto o seu recíproco, ou seja, a relação entre os quadrados se cumpre se, e somente se, o triângulo é retângulo, o que acontece se, e somente se (segundo teorema de Tales e seu recíproco), o terceiro vértice está sobre essa circunferência.
Nota: Neste caso, a informação fornecida pelo mapa é similar à fornecida pelos comandos EquaçãoLugarGeométrico e Prove. Se chamarmos a, b e c aos lados opostos respectivamente aos vértices A, B e Γ, o comando EquaçãoLugarGeométrico(a² ≟ b² + c², A) devolve a circunferência, enquanto que, se A for um ponto dessa circunferência, Prove(a² ≟ b² + c²) devolve "true".
Às vezes só nos interessa conhecer a posição de um ponto. Aqui vemos, como fundo
de tela, uma vista aérea do centro de Coimbra. Contraímos e distorcemos a imagem
e sobrepomo-la. Segundo o
teorema do ponto fixo de Banach,
qualquer que seja a posição da segunda imagem (sem sair do perímetro da
primeira), existe um único ponto em que ambas coincidem. No entanto, o problema desses teoremas de existência (e neste caso, também de unicidade) é que sua demonstração não indica onde se encontra o ponto fixo (apenas um método de aproximações sucessivas aparece). O nosso scanner esclarece isto simplesmente submetendo os pontos do scanner à mesma transformação. Assim, verificamos que, neste caso, o ponto fixo se encontra (como não 🙂) na estátua de Dom Dinis.
Nota: Usamos traços de quadradinhos em vez de pontos para que o traço não oculte a imagem.
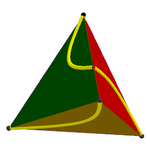
A relação buscada pode ser entre ângulos em vez de distâncias. Esta construção mostra o lugar geométrico dos pontos do plano que formam com ambos os segmentos o mesmo ângulo (ou seja, a partir dos quais ambos os segmentos são vistos sob o mesmo ângulo). O scanner oferece uma forma simples de exibir um exemplo de lugar geométrico intrincado e descontínuo.
Além disso, permite propor facilmente problemas particulares com condições
adicionais do tipo "e se...?". Por exemplo, o que acontece se os segmentos forem
paralelos, ou perpendiculares, ou se seus quatro extremos estiverem nos vértices
de um quadrado, etc.
Esta construção é uma continuação lógica da anterior. Dado o triângulo ABC, aplicamos o scanner com a condição, em cada um dos canais, de que cada par de lados do triângulo seja visto sob o mesmo ângulo. Os três lugares geométricos obtidos, cada um com sua respectiva cor, só se cruzarão no ponto onde os três lados são vistos com o mesmo ângulo (primeiro centro isogônico, X(13)). Se todos os ângulos do triângulo forem menores que 120º, esse ponto estará no interior do triângulo, coincidindo com o ponto de Fermat.
Neste exemplo, temos uma distribuição qualquer de três cargas elétricas positivas (pontos azuis) e três negativas (pontos vermelhos). Se agora introduzirmos uma nova carga, onde ocorrerá o equilíbrio? Ou seja, em que posições a resultante (soma vetorial) das seis forças (atrativas e repulsivas) exercidas pela nova carga sobre as seis cargas existentes será nula?
O scanner mostra, em branco, as posições de equilíbrio. Mas também nos diz que áreas brancas maiores são melhores opções, pois indicam mais pontos onde o todo não fica demasiado desequilibrado; são áreas mais "estáveis".
Nota: A imagem resultante corresponde à introdução de uma nova carga negativa. Se fosse positiva, a mesma imagem seria obtida, apenas trocando os tons azuis por vermelhos e vice-versa. As zonas de equilíbrio brancas permanecem, portanto, inalteradas.
Ao contrário dos métodos usados para representar curvas em programas como o GeoGebra, o scanner não usa algoritmos de rastreamento, portanto não sofre com "exceções". Aqui vemos que alguns pontos de certas curvas podem não ser visíveis com o método usual de traçado. O scanner pode ser útil para torná-los novamente visíveis.
No primeiro exemplo, a origem das coordenadas não aparece como ponto da curva y³ - x³ + 4y² + 2x² = 0 em sua representação gráfica habitual. No segundo exemplo, toda um ramo da curva x⁶ + 3x⁴y - 4y³ = 0 não é visualizado. No terceiro, toda a curva x⁶ - 2x³y + y² = 0 permanece oculta. Nestes pontos ocultos, a curva se anula sem mudar de sinal, o que "confunde" o algoritmo de traçado de curvas implícitas do GeoGebra e de outros programas de álgebra computacional.
Nota: Algebricamente, o primeiro polinômio, quando y = 0, se fatora como (-x + 2) x². O segundo polinômio pode ser fatorado como (x² - y) (x² + 2y)². O terceiro como (x³ - y)².
Vejamos outro exemplo geométrico. Os scanners em que cada ponto faz parte de uma construção geométrica costumam ser mais lentos do que aqueles que comparam expressões algébricas, pois cada linha da folha de cálculo precisa reproduzir a construção geométrica.
Neste exemplo vemos como visualizar relações como a convergência de várias retas (ou semelhantes, como o alinhamento de vários pontos). Em particular, nos interessa saber quando quatro retas de Euler passam pelo mesmo ponto.
Para isso, partimos de um triângulo ABC, que consideramos fixo, e adicionamos um quarto ponto livre D. Criamos as retas de Euler dos triângulos ABD, ACD e BCD, e seus pontos de interseção com a reta de Euler de ABC. As retas serão concorrentes quando a distância entre esses pontos for nula. Sabemos que um dos pontos que procuramos é o incentro, uma vez que as rectas de Euler dos quatro triângulos se encontram, neste caso, no ponto de Schiffler. Mas onde estão os restantes pontos, se é que existem mais?
Todas essas informações apontam para a circunferência circunscrita ao triângulo ABC e para a cúbica de Neuberg como o lugar geométrico ao qual deve pertencer o quarto vértice D para que as retas de Euler do quadrilátero ABCD sejam concorrentes. Podemos concluir, assim, que para satisfazer essa condição, o quadrilátero ABCD deve ser cíclico ou ter um de seus vértices pertencente à cúbica de Neuberg determinada pelos outros três.
Muitas vezes, o gráfico do lugar que aparece ao passar o scanner é difícil de algebrizar com exatidão. Mas mesmo que o nosso objetivo seja obter a expressão algébrica de um lugar geométrico, a visualização proporcionada pelo scanner facilita muito essa busca. A forma da curva ou os traços visualizados ajudam a compreender a natureza do lugar e a identificar pontos notáveis ou singulares.
Neste exemplo, a passagem do scanner encontra a bissetriz entre duas curvas, ou seja, o lugar geométrico dos pontos do plano equidistantes de ambas (Adamou, 2013). Neste caso, formado por dois arcos elípticos. O resultado permite-nos calcular dois arcos de elipse muito próximos do local desejado, que pode ser suficiente em muitas aplicações (arquitetura, robótica, etc.).
Neste exemplo, usamos os canais HSL (ver Apêndice II) para variar a cor do diagrama de bifurcação da aplicação logística xn+1 = r xn (1 - xn) à medida que o coeficiente r aumenta de 2.9 até 4 (com x₀ entre 0 e 1, por exemplo 0.4). O estudo desta equação foi um dos detonadores do nascimento da Teoria do caos.
Como o GeoGebra permite exportar e importar imagens, podemos usar os gráficos obtidos como fundo da tela para realizar explorações sobre eles.
Podemos exportar a vista gráfica para diferentes iterações e visualizá-las
sequencialmente. Assim, é possível ver como o fractal se forma. Também podemos observar como as séries de potências formam, para cada número complexo, polígonos, espirais e outras formas geométricas.
O conjunto de Mandelbrot não é o único fractal que podemos escanear. Serve qualquer fractal gerado por iterações sucessivas em cada ponto (definido como número complexo), como os conjuntos de Julia. Por exemplo, podemos gerar um fractal de Newton generalizado. (Veja-se a sua criação no Anexo I.)
Projeção de uma mistura de garfos, facas e colheres. Lunch With a Helmet On (Almoço com capacete), Shigeo Fukuda (1987).
A fórmula de Euler estabelece a relação fundamental entre as funções trigonométricas e a função exponencial complexa. Richard Feynman chamou essa igualdade de a mais notável da matemática:
exi = cos(x) + i sen(x)
Também podemos visualizar o módulo como superfície e a fase como cor. Esta representação é conhecida como "domínio colorido" (Breda, Trocado & Santos, 2013). Para realçar as mudanças de cor, os canais RGB são substituídos por HSL. Também podemos adicionar linhas de contorno.
A ideia consiste em associar um padrão de cores
a um retângulo do plano complexo (padrão que podemos observar na vista XZ da
função f(z) = z) e observar sua transformação (rotação, reflexão, etc.) ao
aplicar outra função complexa, como a da seção anterio. No caso da função f(z) = ezi, podemos observar que a fase depende apenas da parte real de z.
Da esquerda para a direita, as imagens dos
domínios coloridos de cos(z), i
sin(z) e ezi.
Traço de tempo
Assim como podemos criar uma lista de posições, graças ao comando ObterTempo() podemos criar uma lista que armazene os dados de tempo decorrido em tempo real. Isso permite simular experimentos de cinemática sem utilizar fórmulas ou caminhos predefinidos (Losada, 2024). Vejamos alguns exemplos (mais alguns exemplos, como a Tautocrônica ou a Braquistocrônica, podem ser observados no Apêndice III).
O movimento de queda livre é rápido demais para ter sido medido com precisão na época de Galileu. Com o uso do plano inclinado, que reduz a velocidade da queda, Galileu pôde realizar medições suficientemente exatas para concluir que a velocidade de queda varia uniformemente com o tempo.
Neste exemplo, o traço é triplo: o traço de tempo permite medir o período do pêndulo, o traço de cor dinâmica visualiza as variações de velocidade (máxima para o vermelho), e um ponto traça o gráfico do deslocamento angular em função do tempo. Tudo isso sem o uso de trigonometria ou equações diferenciais.
Usamos HSL para destacar as mudanças de cor. O registro do tempo permite verificar que, em geral, o simples pêndulo não segue um Movimento Harmônico Simples (MHS). Ele só se aproxima bastante desse comportamento quando a amplitude angular é pequena (menor que 10°). Mesmo para 45°, os gráficos ainda são semelhantes. À medida que aumentamos a amplitude, vemos que o gráfico se afasta do comportamento senoidal.
A partir de 130°, o cálculo teórico do período exige números muito grandes, dificultando sua precisão no GeoGebra. Mesmo assim, a animação se ajusta bem ao modelo ideal. Para amplitudes maiores que 175°, o período continua aumentando e tende ao infinito conforme a amplitude se aproxima de 180°.
Se colocarmos um pêndulo na extremidade móvel de outro, obtemos um duplo pêndulo. Embora cada pêndulo obedeça ao período regular de um movimento ordenado, o movimento combinado é caótico.
Podemos usar a poligonal gerada pelo traço para estimar o comprimento do caminho percorrido pelo segundo pêndulo. Também utilizamos canais HSL para adicionar um segmento cujo traço se torna mais claro quanto maior for a velocidade.
Podemos visualizar o efeito dominó ligando uma série de pêndulos. Podemos também verificar que a velocidade de propagação do movimento não é proporcional à gravidade. Embora a gravidade à superfície da Terra seja cerca de seis vezes maior do que na superfície lunar, a velocidade de propagação na Terra é apenas cerca de duas vezes maior, ou menos, do que na Lua (quanto menor for a distância entre as peças, menor será a diferença).
Há exactamente 10 anos surgiu a notícia da inauguração (a 25 de Outubro) do pêndulo de Foucault na Universidade de Coimbra.
Aplicando uma escala de tempo de 1:3600, podemos visualizar uma rotação completa da Terra em apenas 24 segundos (mas apenas colocando o pêndulo num dos polos). Essa escala permite observar o comportamento do pêndulo de Foucault em qualquer ponto do planeta. No hemisfério norte, a rotação aparente do plano do pêndulo será retrógrada (sentido horário); no hemisfério sul, será direta (sentido anti-horário).
O passar do tempo também deixa traço em outros astros, além da Terra. Conhecer a posição do Sol, da Lua e das estrelas pode indicar em que ponto da Terra estamos num determinado momento.
É possível escolher o fuso horário (dentro de três dias, Portugal muda de UTC+1 para UTC+0), a data e a hora (ou clicar em "Agora"), ou um solstício ou equinócio. Também é possível mover até 3 pontos (A, B e C) sobre a esfera terrestre (aparecerá uma etiqueta com a cidade mais próxima, Coimbra ou outra capital ou cidade com mais de um milhão de habitantes; ao clicar no texto, o ponto vai para essa localização).
Ptolomeu denominava de Cosmografia a combinação de Matemática, Geografia e Astronomia usada para representar o mundo. Seu estudo foi essencial desde os primórdios da Idade Moderna, quando os navegadores espanhóis e portugueses precisavam desses conhecimentos para cruzar com sucesso o oceano Atlântico.
Com scripts, podemos transmitir qualquer ação de um objeto para outro... e vice-versa. Neste exemplo, a posição de um ponto no globo terrestre (superfície esférica na vista 3D) é transferida para sua correspondente no mapa de Mercator (vista 2D), e vice-versa. Assim, qualquer traço do primeiro ponto se torna o traço correspondente do segundo, e vice-versa.
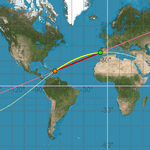
Nesta construção podemos observar a diferença entre as curvas ortodromia (caminho mais curto) e loxodromia (rumo constante). Lembremos que o descobridor da loxodromia foi Pedro Nunes, brilhante matemático português do século XVI, que passou seus últimos 34 anos aqui, em Coimbra (onde hoje um centro tecnológico e uma rua partilham o seu nome). Nunes percebeu que essa curva não era, em geral, uma circunferência, mas sim uma hélice esférica.
Como Nunes e os famosos exploradores e descobridores teriam adorado poder brincar com uma construção como esta! (A imagem seguinte encontra-se no Parque Portugal dos Pequenitos, aqui em Coimbra, um dos primeiros parques em miniatura do mundo; geralmente, uma criança reconhece um mapa-mundo antes de saber multiplicar. E, se mais Mundo houvera, lá chegara, Luís de Camões, Os Lusíadas, VII-14, último verso.)
Conclusão
Graças à observação de todos esses traços, o GeoGebra nos ajuda a explorar
as relações matemáticas no plano, no espaço e até no tempo.
Agradecimentos
Antes de tudo, desejo expressar meu agradecimento especial ao professor José Manuel dos Santos e, de modo geral, ao comitê organizador deste congresso, por me convidar a participar.
Como já é habitual, também quero agradecer ao professor Tomás Recio por seu interesse, conhecimento e apoio, durante muitos anos, em diversos aspectos dos temas aqui tratados.
Agradeço também à
Mariló Fernández Mira as fotos dos arcos e rosáceas do claustro da Sé
Velha em Coimbra.
O autor
Bibliografia e referências
Apêndice I (traço de cor)
Um exemplo típico do uso do traço é a visualização de famílias de curvas ou retas. Neste exemplo, a visualização é dupla. À esquerda, é a função y = sen(x + k) que varia o valor de k, enquanto o ponto de tangência se mantém em x = 0. À direita, é o ponto P da curva y = sen(x) que se desloca.
As tangentes em x = 0 das curvas das funções f(x) = sen(x + k) são as retas y = cos(k) x + sen(k). A envolvente dessa família de retas é a hipérbole equilátera y² - x² = 1, cujas assíntotas são as retas y = ±x (k = 0 ou k = 𝜋).
Assim, para o ponto P, o traço das retas (k = x(P)), delimitado por essas assíntotas, formará uma grade no plano. Podemos também construir a grelha directamente usando Sequência(Reta((k 𝜋, 0), (k 𝜋 + 1, cos(k 𝜋))), k, -10, 10).
Apêndice II (traço dinâmico)
Podemos utilizar coordenadas cartesianas como parte da condição de cada canal RGB, permitindo-nos dividir o ecrã em diferentes zonas de acordo com os nossos interesses.
Se em cada canal RGB colocarmos a função random(), que gera um número aleatório entre 0 e 1, obtemos uma imagem em que a cor de cada pixel é independente do vizinho. Isso é chamado de ruído branco, a conhecida imagem (em tons de cinza nas TVs em preto e branco) produzida pelas antigas televisões analógicas quando não sintonizavam nenhum canal.
Entretanto, se em um dos canais RGB (por exemplo, o verde) substituirmos random() por uma expressão algébrica, o gráfico correspondente se destacará sobre o fundo caótico. Neste exemplo, a expressão para o canal verde é e-|c|, onde c = |P-A| |P-B| |P-C| - 25, ou seja, um oval de Cassini generalizado para três pontos A, B e C.
Embora normalmente não seja necessário, se quisermos diferenciar mais de três objetos por cores, podemos substituir os canais RGB por HSL (Tonalidade, Saturação, Luminosidade). A gestão é um pouco mais complexa. Neste exemplo, diferenciamos as circunferências de raio r e centros A, B, C, D e E com as seguintes expressões: Tonalidade: 0.1exp(-5||P-B|-r|) + 0.2exp(-5||P-C|-r|) + 0.4exp(-5||P-D|-r|) + 0.5exp(-5||P-E|-r|) Saturação: 1 Luminosidade: 0.5 (exp(-5||P-A|-r|) + exp(-5||P-B|-r|) + exp(-5||P-C|-r|) + exp(-5||P-D|-r|) + exp(-5||P-E|-r|))
Substituir a
função exponencial nos canais de cor por outras expressões pode gerar
imagens inesperadas. Neste exemplo, nós a substituímos por uma fração que
nem sempre assume um valor finito (pontos em preto).
Neste caso, criamos um triângulo traçando três tangentes a uma circunferência. Medimos a sua área, 30 u². Dois vértices estão sobre uma linha horizontal (y = -2). Queremos saber onde deve estar o terceiro vértice para que se mantenham tanto a circunferência inscrita quanto a área do triângulo (mantemos uma tangente horizontal porque consideramos equivalentes os triângulos congruentes).
Nota: Algebricamente, vemos os pontos (x - y, x y + 1) 2/(x y - 1), onde (x, y) é um ponto da curva 2 x² y + 2 x y² - 15 x y + 15 = 0.
Podemos gerar um fractal de Newton generalizado. As iterações sucessivas são:
zn+1 = zn + a p(z)/p'(z)
Escolhemos o polinômio complexo p(z) = (z² + 9)(z - 4) e o número a = 1 + i. As raízes do polinômio (pontos atratores) são os pontos vermelho, verde e azul. Cada ponto do fractal é colorido conforme a distância (após várias iterações) às raízes, adquirindo a tonalidade correspondente à raiz para a qual converge.
Apêndice III (traço de tempo)
Estas animações simulam o movimento em tempo real, ignorando o atrito. Não utilizam fórmulas (nem trigonometria, nem equações, nem cálculo diferencial); simplesmente fazem as alterações necessárias nos vetores que direcionam o movimento.
A carga de uma tirolesa ideal (sem atrito) se comporta de forma semelhante à de um pêndulo duplo. A diferença é que agora a polia (o primeiro pêndulo) não traça um arco circular, mas sim um arco de catenária. Ao pendurar uma carga, a polia divide o cabo em dois arcos de catenárias diferentes. Se o peso da carga for grande, esses arcos são praticamente retilíneos (embora fisicamente nunca sejam totalmente), e a polia percorre um arco de elipse, pois seu caminho é determinado pela soma das distâncias aos extremos A e B do cabo. Como a elipse é uma curva mais simples que a catenária, escolhemos essa aproximação.
Aproveitamos o script do seletor
"anima"
para registrar a velocidade máxima alcançada. Assim, podemos observar que
a carga (ponto vermelho) pode atingir velocidades superiores à da polia
(ponto azul). Na prática, a carga geralmente está próxima da polia, o que
minimiza os balanços, junto com o atrito.
Tautócrona ("tempo igual")
A cicloide é a única curva que possui a propriedade de ser uma curva
tautócrona, ou seja, o tempo que uma massa leva para deslizar sem atrito,
sob gravidade uniforme, até o seu ponto mais baixo é independente do ponto
de partida. Huygens descobriu que esse tempo é 𝜋/2 vezes o tempo de queda
livre a partir da altura do diâmetro do círculo que gera a cicloide. Ou
seja, o período de oscilação dos três pontos é sempre o mesmo.
Braquistócrona ("tempo mínimo")
A cicloide é a curva de descida mais rápida para ir de H até P.
Acrescentamos a circunferência que passa por H, S e P, pois Galileu
acreditava que a braquistócrona deveria ser essa circunferência (linha
verde), mas se enganou (embora não por muito), como se pode comprovar na
construção. Na realidade, o ponto verde realiza um movimento pendular, cujo
período de oscilação é um pouco maior que o da cicloide. O que se torna
muito evidente é que a linha reta está muito longe de ser a melhor opção
(embora melhore quanto maior for sua inclinação, ou seja, quanto mais
próximo P estiver de H).
|
|