|
|
► 2. Creación de materiales estáticos
► 2.3 Tableros
Objetivos
Usaremos GeoGebra para crear rápidamente un tablero para un entretenido juego de estrategia para dos jugadores. Podremos imprimirlo, si así lo deseamos, y también podremos jugar directamente sobre él.
Herramientas y comandos
Usaremos muy pocos recursos, solo las siguientes herramientas y el comando Punto[L].
|
|
Punto |
|
Segmento |
Construcción paso a paso
Primero prepararemos el escenario.
En la Barra de Estilo, desactivamos ver Ejes, activamos ver Cuadrícula y elegimos la tercera opción de atracción a cuadrícula: "Fijado a Cuadrícula".
También cerramos la Vista Algebraica.
- Ahora construimos los puntos que harán las veces de casillas con la
herramienta
 Punto,
siguiendo el patrón que indica la imagen. Los puntos creados se nombrarán
automáticamente como A, B, C, ..., O. Seleccionamos todos los puntos (Menú
Edita, Propiedades, hacer clic sobre "Punto" en el panel izquierdo), les
asignamos color gris (pestaña Color), tamaño máximo (pestaña Estilo, valor 9)
y los fijamos (pestaña Básico, "Objeto Fijo").
Punto,
siguiendo el patrón que indica la imagen. Los puntos creados se nombrarán
automáticamente como A, B, C, ..., O. Seleccionamos todos los puntos (Menú
Edita, Propiedades, hacer clic sobre "Punto" en el panel izquierdo), les
asignamos color gris (pestaña Color), tamaño máximo (pestaña Estilo, valor 9)
y los fijamos (pestaña Básico, "Objeto Fijo").
- Con la herramienta
 Segmento
unimos esos puntos como indica la figura.
Segmento
unimos esos puntos como indica la figura. - Creamos la lista {A,B,C,D,E,F,G,H,I,J,K,L,M,N,O} (se nombrará como lista1) para definir el recorrido permitido a las fichas.
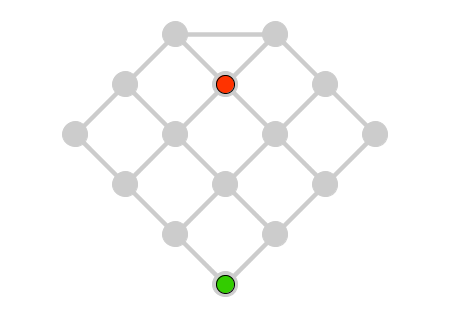
- Con el comando Punto[L] creamos dos "puntos gordos" más, que harán las veces de fichas (roja y verde), y los colocamos en las posiciones iniciales del juego:
P = Punto[lista1]
Q = Punto[lista1]
- Seleccionar la herramienta
 Elige y mueve
(o pulsar
la tecla Esc). Probar a mover las fichas por el tablero.
Elige y mueve
(o pulsar
la tecla Esc). Probar a mover las fichas por el tablero. - Por último, ocultamos la Cuadrícula.
Ejemplo de construcción
|
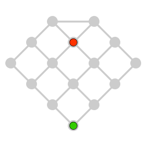
Reglas del juego: Cada jugador mueve por turno su ficha a una casilla adyacente, siguiendo las líneas. El primer jugador en mover es el de la ficha roja y su objetivo es tratar de caer en la casilla en donde se halle el segundo jugador, quien debe tratar de huir. El que consiga su objetivo, gana.
Para evitar partidas "eternas", el primer jugador dispone de cinco minutos para alcanzar su objetivo: en caso contrario, pierde; si un jugador tarda más de 20 segundos en realizar su movimiento, también pierde.
Si ambos jugadores son expertos, el primer jugador, con la ficha roja, puede ganar siempre. ¿Cómo? |
|
Clic en esta imagen abre la construcción de GeoGebra |
|
|
|
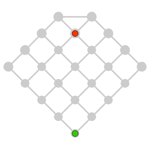
Realizar una construcción similar con un tablero análogo de orden una unidad mayor: |
Comentarios
La mejor forma de comprobar que hemos realizado una construcción como deseábamos es intentando mover todos los objetos y observando su comportamiento. En particular, debemos evitar cometer alguno de estos errores:
- Nos olvidamos de fijar puntos, y usamos un punto del tablero como ficha (con lo que al mover la ficha, el tablero se descompone).
- Colocamos algunos puntos del tablero fuera de la cuadrícula.
Existe una multitud de juegos y rompecabezas sobre sencillos tableros que podemos diseñar fácilmente con GeoGebra. La relación entre los juegos de mesa y las matemáticas ha dado lugar a extensos y profundos estudios. Las conexiones son muchas y muy importantes.
En el caso de los juegos de estrategia pura (como el ajedrez, el go o las damas), se requiere observación, análisis, memoria, intuición y deducción.
En el caso de los juegos de azar puro (como las ruletas y dados), se requiere una buena estimación de las probabilidades y de la esperanza matemática.
En el caso de los juegos mixtos (que son los más populares: parchís, naipes, dominó, mahjong, backgammon...) algo de todo eso y... bastante tiempo libre.
Además, contamos con una amplia variedad de pequeños juegos (como el sencillo ejemplo que aquí hemos elegido) especialmente concebidos para desarrollar la observación y el método, dos de las más valiosas cualidades necesarias para el buen hacer matemático, con la gran ventaja de que no se precisan grandes inversiones de tiempo para su análisis y experimentación.
![]() Investigación:
Investigación:
- Buscar en Internet juegos de lógica y estrategia susceptibles de ser propuestos a los alumnos, ya sean juegos para dos jugadores o solitarios, con reglas sencillas y claras.
- En este juego las formas ceden importancia a favor de la distribución de nodos y conexiones. Es una interesante propuesta crear tableros equivalentes con otras formas, como este:
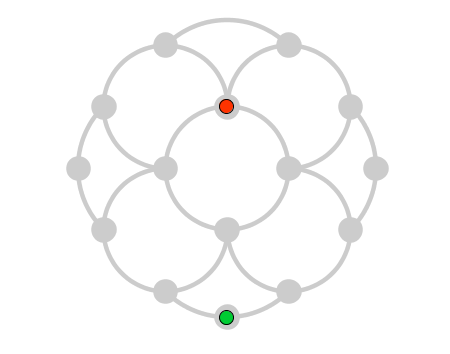
Clic en esta imagen abre la
construcción de GeoGebra