Objetivos

Aunque no es muy frecuente, de cuando en cuando nos encontramos con personajes que brillaron en el mundo de la política y también hicieron algunos pinitos en el campo de las ciencias.

Uno de ellos fue Napoleón Bonaparte. Se cuenta que desde pequeño mostró su interés por las matemáticas, logrando así destacar en el colegio militar y convertirse en oficial de artillería, área en la que el uso de esta ciencia resulta fundamental.

Posiblemente ese interés hacia las matemáticas fue el motivo por el que, una vez iniciada su carrera política, mantuvo contactos con matemáticos muy importantes de su época, como Laplace, Lagrange y Fourier.

El objetivo de esta actividad es realizar una construcción que nos permita conocer uno de los teoremas geométricos que se le atribuyen a Napoleón.

¿Teorema de Napoleón?

Construye un triángulo cualquiera ABC. Sobre cada uno de los lados de este triángulo construye, a su vez, un triángulo equilátero hacia el exterior. Halla ahora los centros de estos nuevos triángulos y únelos: obtendrás un triángulo equilátero.

Con ayuda de las herramientas de GeoGebra podremos realizar sin mayores dificultades la construcción que se propone y comprobar que el triángulo que finalmente obtenemos es equilátero. Al cambiar las condiciones iniciales, es decir, al mover alguno de los vértices A, B o C del triángulo inicial, podremos comprobar la consistencia de la construcción.

La construcción

Primero preparamos el escenario:

• Usando la Barra de Estilo ocultamos los Ejes y la Cuadrícula.
• Elegimos la última opción de Atracción a Cuadrícula: "Desactiva".
• También cerramos la Vista Algebraica dejando únicamente la Vista Gráfica. Otra alternativa es usar la Barra de menús y seleccionar la opción Geometría en el menú Disposiciones.

Si hemos actuado con anterioridad sobre la vista gráfica, también es aconsejable (con clic derecho sobre ella) asegurar la "Vista Estándar".

• Con la herramienta  Punto colocamos los puntos A, B y C en la vista gráfica. Usando la Barra de Estilo elegimos para los puntos A, B y C un color azul oscuro y un tamaño mayor del estándar. Nos facilitará su identificación cuando hayamos completado la construcción.  
• Con la herramienta  Polígono, creamos el triángulo ABC. Usando la Barra de Estilo elegimos para el triángulo un color ocre, un grosor para los lados algo mayor del estándar y un sombreado de un 40%. Nos facilitará su identificación cuando hayamos completado la construcción.
• Con la herramienta Polígono regular creamos un triángulo equilátero sobre cada uno de los lados del triángulo ABC, de modo que en todos los casos el triángulo creado quede orientado hacia el exterior del triángulo ABC. Usando la Barra de Estilo elegimos un color azul, un grosor algo mayor del estándar y un sombreado del 25% para los tres triángulos que hemos construido. También ocultamos en cada triángulo el vértice que no pertenece al triángulo inicial.

Ahora tenemos que determinar los centros de los tres triángulos que hemos construido sobre los lados del triángulo ABC. Al tratarse de triángulos equiláteros, podemos encontrar el centro a partir de las mediatrices de los lados, de las medianas, de las alturas o de las bisectrices de sus ángulos. Vamos a ponerlo en práctica, utilizando herramientas diferentes para cada uno de los centros.

• Con la herramienta Mediatriz trazamos las mediatrices de dos de los lados del triángulo que hemos construido sobre el lado AB del triángulo inicial. Con la herramienta Intersección creamos el punto de corte de las mediatrices.

  El centro así hallado (circuncentro ) equidista de los vértices.

• Con la herramienta Bisectriz trazamos las bisectrices de dos de los ángulos del triángulo que hemos construido sobre el lado BC del triángulo inicial. Con la herramienta Intersección creamos el punto de corte de las bisectrices.

  El centro así hallado (incentro ) equidista de los lados.

• Con la herramienta Perpendicular trazamos las alturas correspondientes a dos de los lados del triángulo que hemos construido sobre el lado AC del triángulo inicial. Con la herramienta Intersección creamos el punto de corte de las alturas (ortocentro ).

  Podemos comprobar que los tres centros encontrados también se hallan en las medianas (es decir, también son baricentros). Para ello, basta crear el punto medio (herramienta Punto medio o Centro) de cualquiera de los lados y unirlo con el vértice opuesto a ese lado (herramienta Recta).

• Usando la Barra de Estilo elegimos para las mediatrices, bisectrices y alturas que hemos trazado un color gris y estilo de línea discontinua. Para los puntos elegimos un color blanco y sin rótulo.
• Con la herramienta  Polígono, creamos el triángulo que determinan los centros de los triángulos equiláteros construidos sobre los lados del triángulo ABC. Usando la Barra de Estilo elegimos para este triángulo un color verde, un grosor para los lados bastante mayor que el estándar y un sombreado del 50%. Nos facilitará su identificación cuando hayamos completado la construcción.

Ahora hemos de hacer las comprobaciones oportunas para ver si este triángulo es equilátero. Podemos hacerlo de diferentes formas. Veamos alguna de ellas.

• Con la herramienta Distancia medimos las distancias entre los centros de los triángulos equiláteros construidos sobre los lados del triángulo ABC: el resultado de la medida es el mismo en los tres casos.
• Con la herramienta Ángulo medimos los ángulos del triángulo formado por los tres centros: en los tres casos obtenemos como resultado 60º.

Ahora lo que haremos es comprobar la consistencia de la construcción y verificar que el triángulo formado por los centros de los triángulos equiláteros es también un triángulo equilátero:

• Mueve alguno de los puntos A, B o C. Estudia diferentes casos y comprueba, en cada uno de ellos, si se verifica el Teorema de Napoleón.

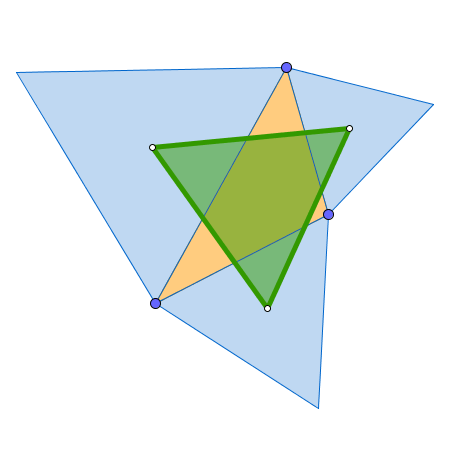
Ejemplo de construcción

Propuesta de trabajo

Averigua si se cumple el Teorema de Napoleón cuando los triángulos equiláteros que se construyen sobre los lados del triángulo original se orientan hacia el interior del triángulo.

Comprueba si el triángulo construido es equilátero utilizando alguna estrategia diferente a las dos que hemos utilizado en el caso anterior.

Comentarios

 Investigación:

•  Calcula las áreas de los triángulos que resultan de unir los centros de los triángulos equiláteros exteriores al triángulo y los interiores. Trata de encontrar alguna relación entre las áreas de estos dos triángulos y la del triángulo de partida.
• ¿Qué ocurre si seguimos el mismo procedimiento a partir de un cuadrilátero? ¿Tiene alguna característica especial el cuadrilátero que se obtiene al unir los centros de los triángulos equiláteros construidos sobre los lados de un cuadrilátero?
• ¿Es realmente Napoleón el descubridor de la relación que hemos analizado? Busca información sobre el tema.