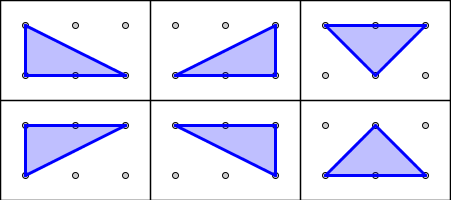
En una retícula cuadrada de 3x2 puntos, ¿Cuántos triángulos distintos, de área 1 unidad cuadrada, podemos dibujar? ¿Y de 0.5 unidades cuadradas?

¿Y si la retícula fuera de 4x2 puntos? ¿Y si fuera de 5x3?

Clic en la imagen para abrir el applet de GeoGebra

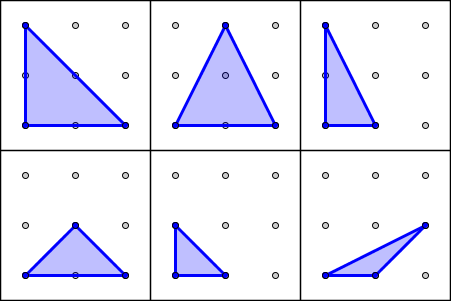
En una retícula cuadrada de 3x3 puntos, ¿Cuántos triángulos distintos podemos dibujar? Dibújalos y clasifica todos los que encuentres.

Clic en la imagen para abrir el applet de GeoGebra

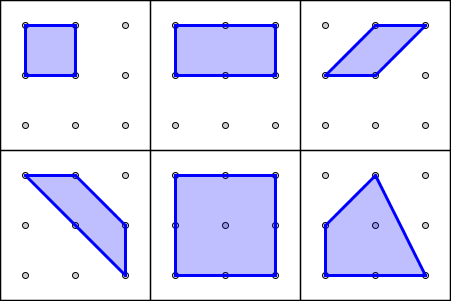
En una trama cuadrada de 3x3 puntos, ¿cuántos cuadriláteros distintos podemos dibujar con la condición de que sus vértices sean puntos de la trama? Dibújalos y clasifica todos los que encuentres.

Clic en la imagen para abrir el applet de GeoGebra

 Estrella

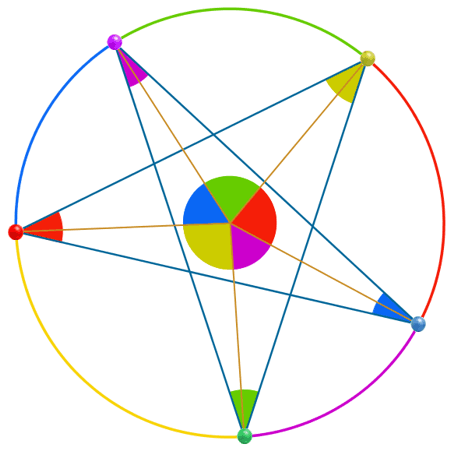
Construimos un polígono estrellado de 5 puntas inscrito en una circunferencia. ¿Qué relación hay entre los ángulos formados en las puntas de la estrella? ¿Se mantendrá constante su suma? En caso afirmativo, ¿sabrías justificar por qué?

Clic en la imagen para abrir el applet de GeoGebra

En una trama cuadrada de 2x2 puntos, ¿cuántos segmentos de distinta longitud podemos construir, con la condición de que sus extremos sean puntos de la trama? ¿Y en una de 3x3 puntos? ¿Y en una de 4x4 puntos?...

Clic en la imagen para abrir el applet de GeoGebra

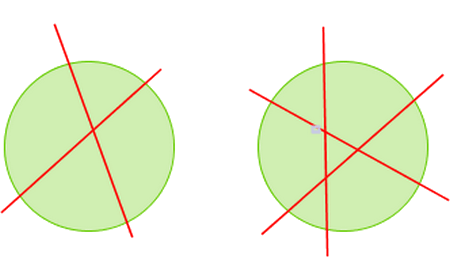
Tienes un pastel de forma circular y un cuchillo. ¿En cuántos trozos puedes dividirlo con un solo corte? ¿Y con dos cortes? ¿Y con tres? ¿Y con cuatro?... Suponemos que en todos los casos los cortes son perpendiculares a la base del pastel.

Clic en la imagen para abrir el applet de GeoGebra

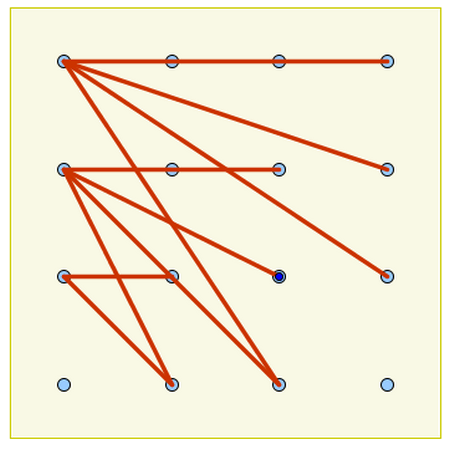
Si unimos un vértice de un polígono con todos los demás, ¿cuántas diagonales se forman? ¿Cuántas diagonales tiene, en total, un polígono?

Clic en la imagen para abrir el applet de GeoGebra

Sobre una retícula cuadrada forma un cuadrado con 4 puntos. Ahora transforma ese cuadrado en un triángulo moviendo el menor número de puntos adyacentes posibles. ¿Cuántos has tenido que mover?

Ahora haz un cuadrado más grande, utilizando 9 puntos. Transfórmalo en un triángulo moviendo el menor número posible de puntos adyacentes. ¿Cuántos has tenido que mover?

Haz otros cuadrados y transfórmalos en triángulos, moviendo siempre el menor número posible de puntos adyacentes. ¿Cuántos tienes que mover cada vez? ¿Cuántos tendrías que mover si el cuadrado está formado por 25 puntos? ¿Y si está formado por 100 puntos?

Clic en la imagen para abrir el applet de GeoGebra

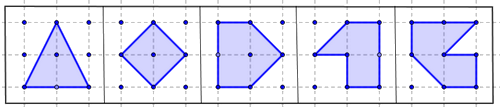
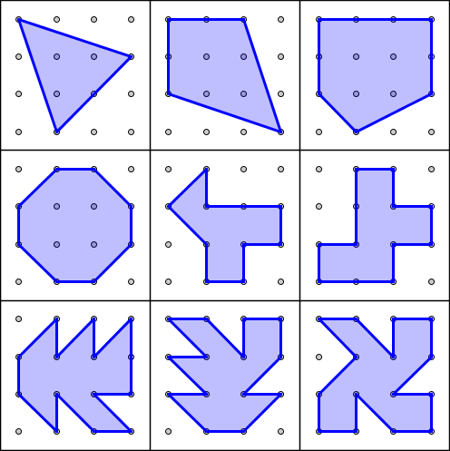
En una trama cuadrada de 3x3 puntos pueden formarse polígonos de 3, 4, 5, 6 y 7 lados, teniendo en cuenta que los vértices sean siempre puntos de la trama. Aquí tienes unos cuantos ejemplos:

Haz tus propios polígonos de 3, 4, 5, 6 y 7 lados en una trama cuadrada de 3x3 puntos.

Investiga ahora qué polígonos puedes formar en una trama cuadrada de 4x4 puntos. Trata de formar polígonos de 3, 4, 5, 6, 7, 8, 9, 10 y más lados. ¿Cuál es el número mayor de lados que puede tener un polígono construido en una trama de 4x4 puntos?

Investiga ahora qué polígonos puedes formar en una trama cuadrada de 5x5 puntos.

Clic en la imagen para abrir el applet de GeoGebra