Objetivos

Uno de los procedimientos clásicos de la geometría sintética es el trazado de las alturas de un triángulo. El objetivo que nos planteamos en esta actividad es llevar a cabo el proceso inverso, es decir, si sabemos que tres rectas concurrentes son las alturas de un triángulo, ¿cómo podemos obtener dicho triángulo? ¿La solución es única? ¿Las relaciones entre esas rectas concurrentes determinan el tipo de triángulo que encontraremos?

El problema

El enunciado del problema que vamos a abordar es el siguiente:

Dadas tres rectas concurrentes, traza un triángulo en el cual las tres rectas son las alturas.

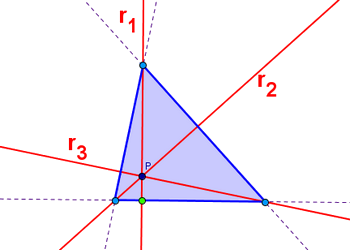
Interpretemos este enunciado: conocemos el punto donde se cortan las alturas del triángulo, es decir, el ortocentro, y también las rectas sobre las que se sitúan las alturas del triángulo. De lo que se trata es de encontrar los triángulos (de mano no sabemos si la solución será única) que cumplan esas condiciones.

Seguramente sacaremos alguna pista para abordar el problema si consideramos el problema resuelto:

Observemos un detalle: una altura, como por ejemplo r₁, es perpendicular a un determinado lado del triángulo, en este caso el dispuesto horizontalmente, pero, además, las otras dos alturas pasan por los extremos de este lado. Dicho de otro modo: los puntos de corte de las otras dos alturas con ese lado determinan los vértices relativos a ese lado.

Así pues, si conociéramos las longitudes de las alturas el problema quedaría de este modo inmediatamente resuelto. Sin embargo no conocemos las longitudes de las alturas, lo cual nos ha de hacer pensar que el problema tendrá más de una solución.

En efecto, si por un punto de una de las alturas (por ejemplo el punto de color verde de la altura r₁), trazamos una perpendicular a la misma, esa recta perpendicular interceptará a las otras dos alturas determinando de ese modo dos de los vértices del triángulo que buscamos. Conocidos esos dos vértices y las alturas sobre los otros dos lados, resulta inmediato determinar el tercer vértice del triángulo.

Pero si tomáramos otro punto en la altura r₁ y siguiéramos el mismo procedimiento, determinaríamos otro triángulo diferente. Por tanto, esto ya nos sugiere que el problema tendrá infinitas soluciones. Pero, ¿cómo serán esas infinitas soluciones? ¿Qué relación tendrán entre sí esos triángulos que obtenemos para cada punto de la altura de la que partimos?

Con ayuda de las herramientas de GeoGebra podremos realizar sin mayores dificultades la construcción para determinar el triángulo que buscamos. La posibilidad que tenemos de mover los puntos libres de la construcción nos va a permitir investigar posteriormente la relación entre las soluciones del problema y también de qué modo  determinan las características del triángulo los datos de partida.

La construcción

Primero preparamos el escenario: usando la Barra de menús seleccionamos la opción Geometría en el menú Disposiciones.

• Con la herramienta Punto creamos el punto A donde se cortarán las tres alturas y otros tres puntos B, C y D que utilizaremos para determinar las alturas.
• Ahora con la herramienta Recta dibujamos las rectas a, b y c, que pasan por los puntos A y B, A y C y A y D, respectivamente.
• Seleccionamos nuevamente la herramienta Punto y hacemos clic sobre un punto de la recta a (la recta que pasa por A y B). De ese modo hemos creado el punto E.
• Con la herramienta Perpendicular trazamos la perpendicular a la recta a por el punto E.
• Con la herramienta Intersección señalamos los puntos de intersección de la perpendicular que acabamos de trazar con las otras dos alturas, es decir, con las rectas b y c. De ese modo determinamos los puntos F y G, que son dos de los vértices del triángulo que buscamos.
• Por el punto F, utilizando la herramienta Perpendicular, trazamos la perpendicular a la altura que pasa por G.
• Por el punto G, utilizando la misma herramienta, trazamos la perpendicular a la altura que pasa por F.
• Con la herramienta Intersección señalamos el punto de intersección H de las dos rectas que acabamos de trazar. Es el tercer vértice del triángulo.

Si alguno de los puntos de intersección cae fuera de la zona visible de la vista gráfica movemos alguno de los puntos que hemos creado hasta conseguir su visualización.

• Finalmente, con la herramienta  Polígono, creamos el triángulo FGH.

Usamos la Barra de Estilo para mejorar la estética de la construcción y dejar más claros los objetos que hemos creado. Elegimos un color rojo y un trazo un poco más grueso que el estándar para las rectas iniciales. Empleamos un color azul, un trazo algo más grueso que el estándar y un sombreado del 25% para el triángulo. Utilizamos un estilo de línea de trazos para las perpendiculares que hemos trazado. Y cambiamos también los colores y tamaños de los puntos, diferenciando los cuatro puntos iniciales, el punto que hemos creado sobre la altura a y los tres vértices del triángulo.

Probamos ahora la consistencia de la construcción e investigamos qué es lo que ocurre si cambiamos los datos iniciales: los puntos A, B, C y D, que determinan el ortocentro y las alturas, respectivamente, y el punto E que hemos tomado sobre la altura a.

• ¿Qué relación guardan entre sí los triángulos que obtenemos cuando cambiamos la posición del punto E?
• ¿Cuál debe ser la disposición de las alturas para que el triángulo obtenido sea isósceles? ¿Y para que sea equilátero?
• ¿Cuál debe ser la disposición de las alturas para que el triángulo sea rectángulo?

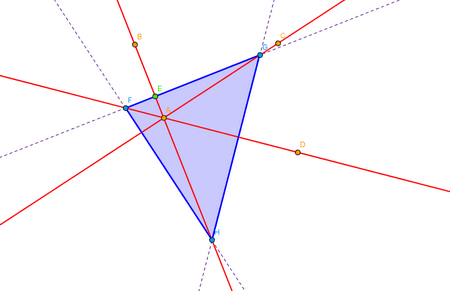
Ejemplo de construcción

Propuesta de trabajo

Dadas tres rectas concurrentes, traza un triángulo del cual las tres rectas son las mediatrices. ¿La solución es única? ¿Cómo determina la posición de las mediatrices las características del triángulo que obtenemos?

Comentarios

 Investigación:

• ¿Podemos determinar el triángulo si las tres rectas concurrentes son sus bisectrices? ¿Y si son sus medianas?
• La cantidad y variedad de relaciones existentes entre los puntos y lugares asociados a un triángulo es realmente impresionante. Están catalogados más de 3.500 puntos notables distintos. Son tantos que, con cierto humor, las siglas del catálogo web que los recopila, en continua expansión, son ETC. Puedes obtener más información en la Encyclopedia of Triangle Centers .