MÓDULO 6

Introducción

Puntos

La plaza

El arco

Viviani

Puntos notables

Otros modelos

 

 


Manual       Imágenes      

 
  • Inicio
  • Módulos
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
    •     

    ► 6. Problemas dirigidos

           ► 6.2 Puntos

    Objetivos

    Pretendemos diseñar un tipo de actividad que permita su uso tanto para profundizar en un determinado concepto como para servir de prueba evaluadora de una competencia concreta. Para ello propondremos un modelo muy sencillo, susceptible de ser adaptado fácilmente a una pluralidad de contenidos.

    Se trata de proponer la manipulación de objetos hasta que cumplan una propiedad. En ese momento, un texto nos avisará que hemos logrado el objetivo.

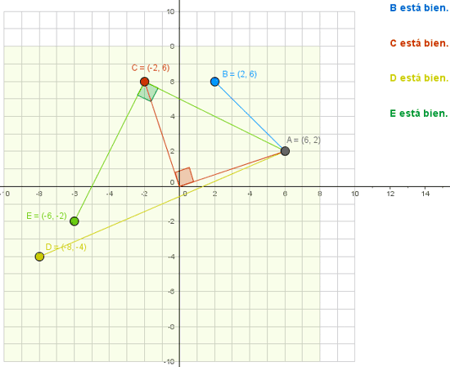
    En este ejemplo, el objetivo consiste en colocar correctamente cuatro puntos respecto a uno dado (punto A). El enunciado es:

    Coloca los puntos B, C, D y E de forma que:

    B debe ser el simétrico de A respecto a la recta y = x.
    C debe ser el resultado de rotar A 90° alrededor del origen.
    D debe ser el simétrico de A respecto al punto (-1, -1).
    E debe ser el resultado de rotar A 270° alrededor de C.

    Las condiciones correspondientes para su posicionamiento correcto serán, por lo tanto:

    B debe coincidir con (y(A), x(A))
    C debe coincidir con (-y(A), x(A))
    D debe coincidir con (-2 - x(A), -2-y(A))
    E debe coincidir con (x(C) - y(C) + y(A), x(C) + y(C) - x(A))

    Bastará variar la posición de A para que la misma construcción ofrezca un nuevo caso particular del mismo problema.

    Herramientas

    No necesitaremos nuevas herramientas. Aparecerá el comando Secuencia, que usaremos para crear una cuadrícula limitada. También usaremos las condiciones de visibilidad para notificar que la posición de cada punto es correcta solo cuando lo sea. Para ello, haremos uso de los operadores lógicos.

    Punto Segmento
    Ángulo Texto

    Para su uso, exportaremos la construcción como un applet de página web.

    Construcción paso a paso

    Antes de empezar, puede ser buena idea echar un vistazo al "Ejemplo de construcción" que se encuentra en esta página. Incluso podemos ayudarnos de la Barra de Navegación para realizar un rápido recorrido por los pasos.

    Primero prepararemos el escenario.

     Preparación

    Sí

    No. En Propiedades de la vista gráfica,  Cuadrícula, activar "Distancia" y establecerla en x:1, y:1.

    Ajusta

    Dibujaremos el "tablero de juego", una cuadrícula limitada.

     Etapa 1

    • Entrada:         

    Secuencia[Segmento[(s, -10), (s, 10)], s, -10, 10]

    Secuencia[Segmento[(-10, s), (10, s)], s, -10, 10]

    • Redimensionamos (rueda del ratón) la vista gráfica hasta ver toda la cuadrícula, asignamos un color gris claro a esas listas y redibujamos los ejes. Entrada:  

    x = 0

    y = 0

    El color claro en la cuadrícula facilitará la percepción de los objetos sobre ella.

     Etapa 2

    • Con la herramienta Punto creamos 5 puntos y los colocamos sobre intersecciones de la cuadrícula. Les damos distintos colores.
    • Introducimos las condiciones de visibilidad, que corresponden a las soluciones del problema:

    testB: B == (y(A), x(A))

    testC: C == (-y(A), x(A))

    testD: D == (-2 - x(A), -2 - y(A))

    testE: E == (x(C) - y(C) + y(A), x(C) + y(C) - x(A))

    • Creamos cuatro puntos de posición para los textos y los ocultamos:

    PB = (12, 10)

    PC = (12, 8)

    PD = (12, 6)

    PE = (12, 4)

    Los puntos de posición de texto nos ayudan a alinear y colocar con precisión los distintos textos.

     Etapa 3

    • Desde el Campo de Entrada (usando comillas) o con la herramienta  Texto (no hacen falta comillas) editamos los siguientes textos, colocándolos en la posición que se indica  (cuadro de diálogo Propiedades):

    "Coloca B." (texto 1) en la posición PB.

    "Coloca C." (texto 2) en la posición PC.

    "Coloca D." (texto 3) en la posición PD.

    "Coloca E." (texto 4) en la posición PE.

    "B está bien."  (texto 5) en la posición PB.

    "C está bien."  (texto 6) en la posición PC.

    "D está bien."  (texto 7) en la posición PD.

    "E está bien."  (texto 8) en la posición PE.

    • En el mismo cuadro de Propiedades, le damos a cada texto igual color que el punto correspondiente y en la pestaña  Avanzado establecemos como condiciones de visibilidad las que aquí se indican:

    Para introducir el operador lógico ! (.NO.) se puede utilizar tanto el teclado como la lista desplegable.

    ! testB para el texto 1.

    ! testC para el texto 2.

    ! testD para el texto 3.

    ! testE para el texto 4.

    testB para el texto 5.

    testC para el texto 6.

    testD para el texto 7.

    testE para el texto 8.

    • Colocamos A en la posición (2, 3), por ejemplo, y el resto de los puntos en posiciones incorrectas.

    Ahora solo falta convertir la construcción en una página web dinámica (applet) y añadir en ella el enunciado del problema.

     Etapa 4

    Coloca los puntos B, C, D y E de forma que:

    B debe ser el simétrico de A respecto a la recta y = x.
    C debe ser el resultado de rotar A 90° alrededor del origen.
    D debe ser el simétrico de A respecto al punto (-1, -1).
    E debe ser el resultado de rotar A 270° alrededor de C.
    • En la pestaña  Avanzado, establecer como Ancho 750, y como Alto 650 píxeles. También se pueden elegir otras opciones, a nuestro gusto.
    • Cuando esté todo como deseamos, pulsamos el botón Exporta. En el cuadro de diálogo Guarda, podemos cambiar el nombre de la página web y elegir la ubicación en el disco duro. Pulsamos Guardar.

    Una vez guardada la página web, cabe la posibilidad de editarla con cualquier editor HTML para mejorarla en lo que deseemos.

     En el caso de que solo se quiera modificar algún detalle del applet no es necesario repetir todo el proceso de exportación; será suficiente con modificar con GeoGebra la construcción (archivo de extensión GGB) que el programa ha creado automáticamente en la misma carpeta donde se ha guardado la página web (archivo de extensión HTML).

    Ejemplo de construcción

     Puntos

    Clic en esta imagen abre la construcción de GeoGebra

     Propuesta de construcción

    Realizar una construcción similar que proponga este enunciado: "B debe ser el simétrico de A respecto a la recta y = -x."
    Comentarios

    Como vemos, resulta sencillo realizar construcciones de autoevaluación para una amplia gama de enunciados, ya sean geométricos o de otra naturaleza. En nuestro ejemplo de construcción, hemos añadido segmentos y ángulos para ayudar a la comprensión de los conceptos implicados. También hemos señalado (zona verde) aquellas intersecciones de la cuadrícula que puede ocupar A de forma que las posiciones correctas del resto de los puntos no queden fuera de ella.

    Otra manera de formular este tipo de problemas es con condiciones que se complementen. Por ejemplo, "colocar el punto P de tal forma que diste 3 unidades de A y a la vez esté en la recta y = x + 4". En algunos casos, como en este ejemplo, puede que haya más de una solución. En tales casos, podemos usar el operador lógico || (.O.) para establecer la condición.

     Investigación:

    • Los enunciados con condiciones de distancia entre puntos pueden originar problemas prácticos al intentar realizar este tipo de construcciones. ¿Por qué?