Lo primero que hay que entender es que las matemáticas son un arte. La diferencia entre las matemáticas y el resto de las artes, como la música y la pintura, es que nuestra cultura no la reconoce como tal.

Paul Lockhart

Dibujos fáciles y precisos

En la Presentación, se contemplaban dos formas generales de usar GeoGebra:

• Herramienta del estudiante: para realizar construcciones desde cero, ya sean dirigidas o abiertas, de resolución o de investigación.
• Herramienta del profesor: para realizar materiales educativos estáticos (imágenes, protocolos de construcción) o dinámicos (demostraciones dinámicas locales, applets en páginas web).

Vamos a fijar ahora nuestra atención en la realización de materiales educativos estáticos por parte del profesor.

Evidentemente, ese no es el fin primordial para el que se desarrolló GeoGebra. Sin embargo, por diversas causas (carencia de ordenadores, limitaciones horarias para usarlos, falta de hábito en el control del espacio informático, etc.), a veces se prescinde completamente de GeoGebra porque se piensa que solo puede ser útil en un aula con ordenadores. Con ello, el profesor renuncia a una cómoda y precisa herramienta con la que crear el material personalizado que a menudo desea presentar a sus alumnos.

En este módulo veremos cómo crear las siguientes imágenes en poco tiempo. Esto nos permitirá, por ejemplo, insertarlas posteriormente en un documento de texto o en una presentación.

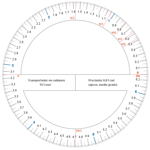
No repararemos en la sencillez o complicación de las herramientas que vamos a usar, por lo que no nos debe preocupar si algún procedimiento nos resulta por ahora especialmente oscuro. Solo queremos mostrar algunos materiales estáticos de diverso tipo creados con GeoGebra, y las pocas instrucciones que hemos necesitado para generarlos.

Particularmente, introduciremos el poderoso comando Secuencia. Si bien este comando es uno de los más difíciles de dominar, es también uno de los que más tiempo y trabajo nos puede ahorrar, por lo que es recomendable que al menos el profesor conozca su existencia desde un principio.

En cualquier caso, aprovecharemos la construcción realizada para, yendo un poco más allá, continuarla de forma que también sea aprovechable como recurso dinámico interactivo.

Sin construir nada, simplemente haciendo un volcado de pantalla al portapapeles (tecla Imp Pant), o mejor aún, exportando como imagen la vista gráfica (Menú Archivo Exporta) con los Ejes o la Cuadrícula visible, ya tenemos una imagen u hoja de trabajo útil como plantilla para proponer cuestiones sobre coordenadas, mallas ortogonales y mallas isométricas.

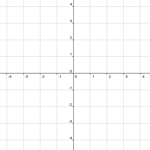
También puede ser buena idea, si tenemos pensado hacer fotocopias, cambiar el color de la Cuadrícula a un gris más oscuro o negro para aumentar el contraste.

Por otra parte, la posibilidad de copiar y pegar objetos permite aumentar rápidamente el número de objetos creados.

Unidades de superficie

El concepto de unidad, como medida de referencia, es fundamental. Para facilitar la comunicación con los alumnos (y entre ellos), en un primer estadio, podemos establecer como unidad de longitud en los Ejes y en la Cuadrícula 1 cm, aunque esta medida no corresponda a "píxeles".

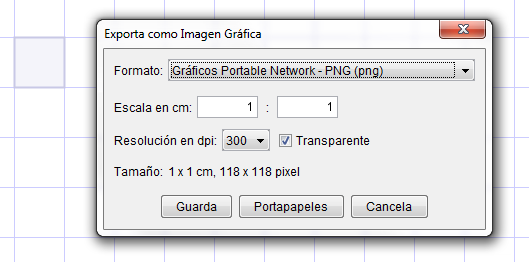
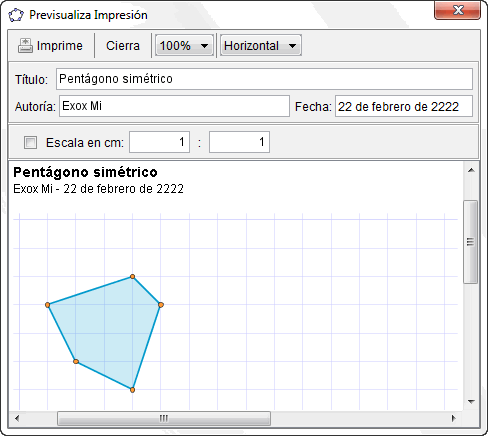
De hecho, en la Cuadrícula por defecto de GeoGebra, si exportamos la imagen como "png" (escala 1:1) y la imprimimos, cada casilla ocupa en el papel exactamente 1 cm². También puede comprobarse directamente desde el Menú Archivo Previsualiza impresión.

Por defecto, con escala de pantalla 1:1, una unidad en los Ejes equivale a 50 píxeles.

Tamaño en papel y tamaño en pantalla.

Por otra parte, el atractivo hacia la Geometría, la más visual de las áreas matemáticas, se ve frecuentemente impulsado por la valoración de la estética de las formas y colores. En todas las construcciones, recomendamos la mejora del acabado estético.

Los ojos de GeoGebra: el ojo gráfico y el ojo algebraico

Desde las primeras actividades mostraremos simultáneamente la vista gráfica y la algebraica. Es importante que, desde el comienzo, nos acostumbremos a visualizar las variaciones que se producen en una de esas vistas cuando interactuamos en la otra. Cuantas más representaciones visuales distintas obtengamos del mismo objeto o relación geométrica, más nítida será la comprensión de su naturaleza y variabilidad, lo que no es óbice para que en determinados momentos o actividades se considere recomendable ocultar la vista algebraica, favoreciendo así la atención en el comportamiento de los objetos gráficos.