|
|
► 3. Creación de recursos estáticos
► 3.+ Otros modelos
Otros ejemplos para observar y analizar
|
Dos listas son suficientes para crear plantillas de papel logarítmico y semilogarítmico. Los objetos libres son parámetros modificables. La forma más sencilla de variar sus valores es hacer clic en el parámetro deseado y pulsar las teclas + o -. |
|
Clic en esta imagen abre la construcción de GeoGebra |
|
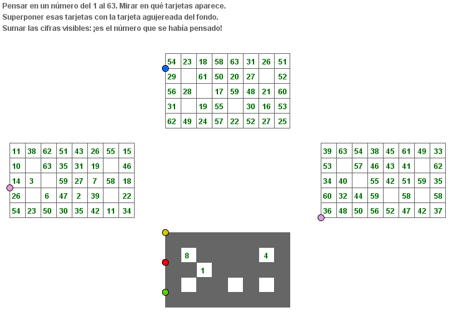
Hemos exportado la imagen como imagen vectorial (tarjetas.eps), la hemos incrustado en Word (tarjetas.doc) y también la hemos convertido a PDF (tarjetas.pdf). |
|
Clic en esta imagen abre la construcción de GeoGebra |
|
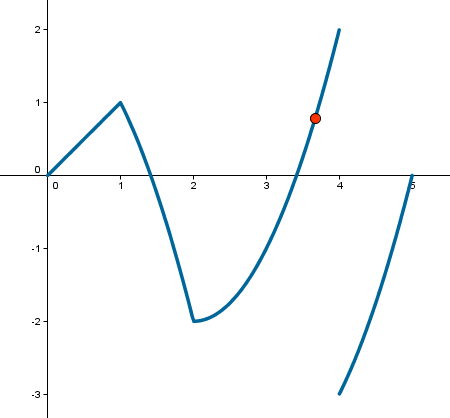
Puede usarse el comando Si para crear una función definida a trozos. |
|
Clic en esta imagen abre la construcción de GeoGebra |
|
Podemos usar
la técnica del Color Dinámico
(ver Módulo 2
En este caso, las líneas de colores se cortarán en el primer punto isogónico (es decir, el punto desde el cual se ven los lados con el mismo ángulo) del triángulo ABC. Este punto coincide con el punto de Fermat si el mayor de los ángulos del triángulo no supera los 120°, y deja de existir en caso contrario.
Damos a cada punto P de la línea de escáner (que trazará el dibujo) el color RGB basado en las diferencias entre los ángulos APB, BPC y CPA. Las posiciones cerca de cumplir APB=CPA se colorearán de rojo, cerca de APB=BPC de verde y cerca de BPC=CPA de azul:
La constante añadida (10) sirve para ajustar la gradación del color. |
|
Clic en esta imagen abre la construcción de GeoGebra |
|
La siguiente construcción dibuja la imagen del conjunto de Mandelbrot
El esquema de construcción de las condiciones de color es el siguiente:
|
|
Clic en esta imagen abre la construcción de GeoGebra
Clic en esta imagen abre la construcción de GeoGebra |