Objetivos

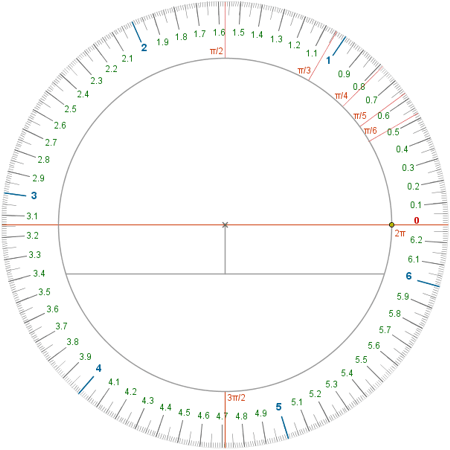
Usaremos GeoGebra para crear rápidamente un transportador de ángulos poco habitual: la unidad será el radián en vez del grado. Mediante su construcción y uso se pretende familiarizar al alumno con esta medida.

En el proceso, aparecerá un comando particularmente útil, el comando Secuencia. Aunque aquí lo usaremos para crear listas de segmentos, este comando crea rápidamente listas de objetos cualesquiera (números, puntos, funciones, curvas...).

Añadiremos a esta construcción dos puntos que nos permitirán trasladar y girar el transportador. Así podremos usarlo también como instrumento dentro de GeoGebra.

Como es habitual, retocaremos a nuestro gusto el estilo de los objetos gráficos.

Herramientas y comandos

En esta actividad crearemos y manejaremos listas. Las listas son colecciones de objetos separados por comas y agrupados por llaves.

Por ejemplo, L = {A, B, C} puede ser la lista (y como tal, un único objeto) de tres puntos.

La sintaxis del comando Secuencia, al que antes nos referimos, es la siguiente:

Secuencia [e(s), s, s₁, s₂, incremento de paso]

donde e(s) es una expresión -numérica o geométrica- dependiente de la variable s, y s₁, s₂ son los valores inicial y final respectivamente que toma la variable s.

El resultado de una secuencia es la lista de todos los valores u objetos {e(s₁), ..., e(s₂)}.

Si no se especifica el incremento de paso, GeoGebra asume que es una unidad.

Además del comando Secuencia, emplearemos los comandos Punto, Centro (o PuntoMedio), Segmento, Circunferencia y Angulo.

Construcción paso a paso

Antes de empezar, puede ser buena idea echar un vistazo al "Ejemplo de construcción" que se encuentra en esta página. Incluso podemos ayudarnos de la Barra de Navegación para realizar un rápido recorrido por los pasos.

Primero prepararemos el escenario.

Creamos el transportador.

Ocultamos el punto B.

Ahora graduamos el transportador con marcas de distinta longitud. A la primera secuencia le daremos más grosor, para destacarla.

Por último, creamos seis marcas más largas para π/6, π/5, π/4, π/3, π/2 y 3π/2.

Para terminar, mejoramos el Estilo.

Ejemplo de construcción

Comentarios

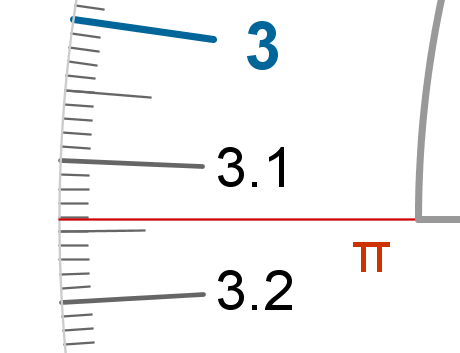
En vez de completar el diseño rotulando las marcas a mano, en el ejemplo que mostramos hemos añadido textos posicionados con precisión. Una imagen preparada para imprimir en una hoja DIN-A4 se puede descargar en este enlace. La siguiente imagen recoge un detalle de esa hoja, en el que podemos apreciar la calidad de las imágenes creadas con GeoGebra:

La clave para añadir los textos reside en la combinación de los comandos Secuencia y Texto:

t1 = Secuencia[t, t, 0, 2pi, 0.1]  (crea los textos numéricos)

t2 = ConservaSi[x ≠ floor(x), t1]  (conserva solo los no enteros)

long = Longitud[t2]

Secuencia[Texto[Elemento[t2,s], A - (0.17, 0.08) + (5.17; a + Elemento[t2,s])], s, 1, long]

El comando Secuencia es un potente comando que puede tener insospechadas aplicaciones. En general, puede ser una buena idea reflexionar si puede ser de ayuda en cualquier situación en la que necesitemos realizar operaciones sobre diversos objetos del mismo tipo (puntos, vectores, números, curvas...)

 Investigación:

• Probar a ejecutar el comando Secuencia refiriéndose a distintos objetos. A continuación, proponemos tres ejemplos (se pueden copiar directamente aquí para pegarlos en el Campo de Entrada). Pensar en algún otro tipo.

Secuencia [s x², s, -0.5, 0.5, 0.02]

Secuencia [(s, 0.5 s²), s, -5, 15, 0.2]

Secuencia [Curva[4 cos(t), 4 sin(s t), t, 0, 2pi], s, 1, 9, 2]