MÓDULO 9

Introducción

Diagonales

Segmentos

Cuadrados

Otros modelos

 

 


Manual       Imágenes      

 
  • Inicio
  • Módulos
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
    •     

    ► 9. ¿Y si...? Curiosidad, intuición y conjeturas

           ► 9.4 Cuadrados

    Objetivos

    Además del razonamiento inductivo, existe otro tipo de razonamiento que suele dar muy buenos resultados al enfrentarnos a problemas de muy diverso tipo. Se trata del razonamiento regresivo. Es decir, razonar a partir de la suposición de que el problema ya ha sido resuelto.

    Mostraremos un ejemplo sencillo. Creamos un simple cuadrado y nos preguntamos si será posible inscribir otro cuadrado en él. También nos preguntamos si es posible trazar más de un cuadrado inscrito.

    Herramientas y comandos

    No usaremos ningún comando ni entrada de directa de operaciones, solo las siguientes herramientas geométricas.

    Punto Intersección Centro
    Recta Segmento Perpendicular
    Polígono Polígono regular Semicircunferencia
    Refleja por punto  
    Construcción paso a paso

    Antes de empezar, puede ser buena idea echar un vistazo al "Ejemplo de construcción" que se encuentra en esta página. Incluso podemos ayudarnos de la Barra de Navegación para realizar un rápido recorrido por los pasos.

    Primero prepararemos el escenario.

     Preparación

    No

    No

    Desactiva

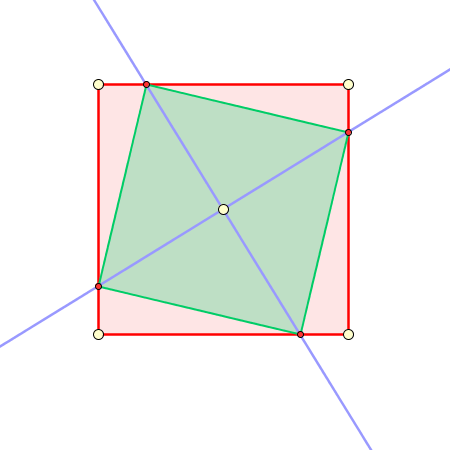
    Dibujaremos una primera solución, que es la que primero suele aparecer.

     Etapa 1

    • Con la herramienta  Polígono regular construimos un cuadrado.
    • Con la herramienta  Centro señalamos los puntos medios de dos lados consecutivos del cuadrado anterior.
    • Con la herramienta  Polígono regular construimos un cuadrado a partir de los dos puntos anteriores.

    Hemos encontrado una solución, un cuadrado inscrito cuya área es exactamente la mitad del cuadrado original.

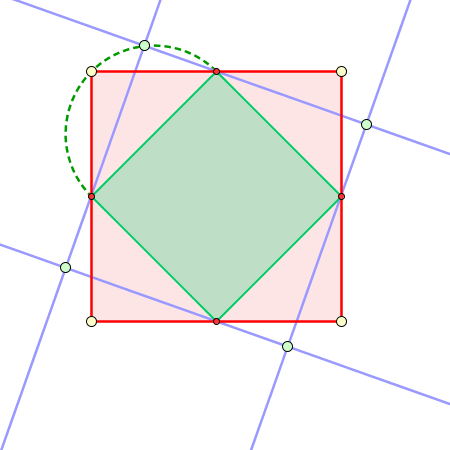
    Nos preguntamos ahora si habrá más soluciones, y cómo construirlas. En vez de atacar el problema de forma progresiva, imaginaremos el problema ya resuelto. Tenemos un cuadrado inscrito en otro. Esto significa que el cuadrado original puede considerarse como circunscrito. Fijémonos en un vértice de ese cuadrado circunscrito. Al ser cuadrado, el ángulo en ese vértice será de 90°. Por lo tanto, se formará un triángulo rectángulo con hipotenusa el lado del triángulo inscrito. Lo que implica que el vértice del cuadrado circunscrito tiene que estar sobre la semicircunferencia que tiene por diámetro el lado del cuadrado inscrito.

     Etapa 2

    • Con la herramienta  Semicircunferencia construimos una semicircunferencia exterior uniendo dos vértices consecutivos del cuadrado inscrito.
    • Con la herramienta  Punto situamos un nuevo punto en esa semicircunferencia.
    • Con la herramienta  Recta unimos el nuevo punto con los extremos de la semicircunferencia.
    • Con la herramienta  Perpendicular completamos el cuadrado circunscrito.

    Observemos que no es lo mismo construir el cuadrado circunscrito que el inscrito, así que todavía no hemos resuelto el problema. Sin embargo, es fácil darse cuenta, variando de posición el punto sobre la semicircunferencia, de la relación existente entre ambos cuadrados. Los vértices del cuadrado inscrito se encuentran siempre situados a la misma distancia (variable entre 0 y la longitud del lado del cuadrado circunscrito) del correspondiente extremo del lado del cuadrado circunscrito donde descansa. Esta observación es suficiente para resolver el problema.

    Ejemplo de construcción

     Cuadrados inscritos (razonamiento regresivo)

    Clic en esta imagen abre la construcción de GeoGebra

     Cuadrados inscritos (solución)

    Clic en esta imagen abre la construcción de GeoGebra

     Propuesta de construcción

    Realizar una construcción similar que inscriba un triángulo equilátero en otro.
    Comentarios

    Por supuesto, lo realmente importante no es el resultado de la cuestión planteada u otras cuestiones similares sino los métodos empleados para obtener soluciones. Heurísticas como el razonamiento inductivo, regresivo y deductivo, unidas a la observación y experimentación, son métodos fundamentales. La facilidad que brinda GeoGebra para explorar y ensayar no solo ayuda en la enseñanza de determinados conceptos o procedimientos, sino que favorece enormemente la curiosidad, el autoaprendizaje y la investigación.

     Investigación:

    • Nos podemos plantear multitud de preguntas relacionadas con polígonos inscritos. ¿Se pueden inscribir triángulos semejantes cualesquiera? ¿Y un cuadrado en un triángulo? ¿Y un cuadrado en un rombo? Etc.