|
|
► 12. Proyecciones 3D
► 12.3 Toro
Objetivos
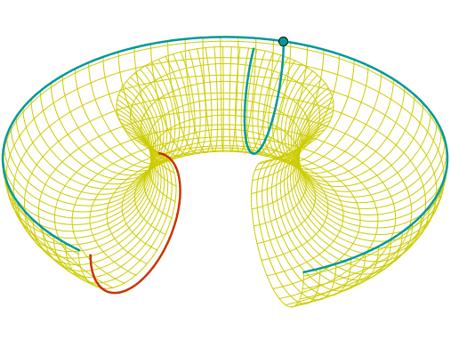
Simularemos la superficie de un toro creando familias de curvas que descansan sobre él.
Un punto tridimensional {px, py, pz} se puede proyectar en la vista gráfica como:
(px sin(β) + py cos(β), -px cos(β) sin(α) + py sin(β) sin(α) + pz cos(α))
donde α y β son los ángulos de inclinación y rotación.
Para simplificar, definimos:
sb = sin(β), cb = cos(β), cs = -cos(β) sin(α), ss = sin(β) sin(α), ca = cos(α)
Con lo que la expresión anterior queda así:
(px sb + py cb, px cs + py ss + pz ca)
Ahora bien, si conocemos las ecuaciones paramétricas de una superficie en el espacio:
(x(u,v), y(u,v), z(u,v))
podemos generar dos familias de curvas sin más que sustituir estas coordenadas en vez de (px, py, pz) en la proyección anterior.
- L1 = Secuencia[Curva[x(u,v) sb + y(u,v) cb, x(u,v) cs + y(u,v) ss + z(u,v) ca, v, v1, v2], u, u1, u2, paso]
- L2 = Secuencia[Curva[x(u,v) sb + y(u,v) cb, x(u,v) cs + y(u,v) ss + z(u,v) ca, u, u1, u2], v, v1, v2, paso]
En la primera lista de curvas, cada curva hace variar únicamente el parámetro v en cada punto. La familia de curvas se obtiene al secuenciar el parámetro u. En la segunda lista, viceversa.
Las constantes u1, u2, v1 y v2 son los valores mínimo y máximo para los que hacemos variar u y v. La constante “paso” se añade para hacer más o menos densa la red de curvas.
En el caso del toro
![]() , la parametrización empleada es:
, la parametrización empleada es:
x(u,v) = (R + r cos(u)) cos(v)
y(u,v) = (R + r cos(u)) sin(v)
z(u,v) = r sin(u)
Construcción paso a paso
Antes de empezar, puede ser buena idea echar un vistazo al "Ejemplo de construcción" que se encuentra en esta página. Incluso podemos ayudarnos de la Barra de Navegación para realizar un rápido recorrido por los pasos.
Preparamos el escenario.
|
|
Para facilitar la percepción espacial, mostraremos solo el punto encargado de mover uno de los ángulos del punto de vista (el ángulo de rotación β).
|
|
Construimos el ángulo β y definimos las variables auxiliares sb, cb, cs, ss y ca:
|
|
Finalmente, creamos las listas de curvas (con algún pequeño ajuste para mejorar la visualización).
|
|
Ejemplo de construcción
|
((R+r cos(u)) cos(v), (R+r cos(u)) sin(v), r sin(u)) |
|
Clic en esta imagen abre la construcción de GeoGebra |
|
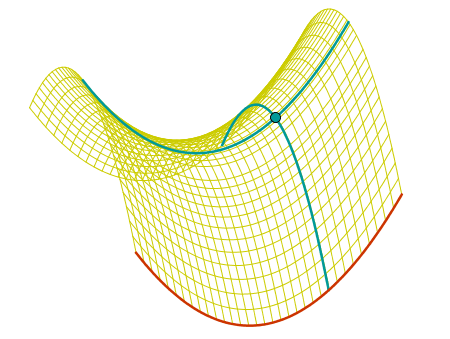
Realizar una construcción similar para un paraboloide hiperbólico ("silla de montar") con la parametrización:
Nota: En la parametrización, se supone que la variable "r" (escala) multiplica a cada componente. |
|
|
Comentarios
En la construcción de ejemplo hemos añadido algunas curvas individuales para potenciar la buena interpretación de la superficie. También hemos convertido las constantes u1, u2, v1, v2 y "paso" en variables que dependen de la posición de algunos puntos en los segmentos que se ven en la parte superior. De esta forma, podemos "abrir" la superficie simplemente arrastrando esos puntos.
![]() Investigación:
Investigación:
- En el apartado "Otros modelos" podemos ver más ejemplos de superficies. Buscar en Internet parametrizaciones correspondientes a otras superficies o curvas espaciales (como las hélices, por ejemplo).