ENTRADA
► Entrada
► Inecuaciones
Inecuaciones
El área (finita o infinita) determinada por un conjunto de inecuaciones es una región.
Podemos introducir en el Campo de Entrada inecuaciones en una o dos variables (x e y). No hay limitaciones en su representación algebraica, pero solo algunos tipos de inecuaciones pueden aparecer representadas en la vista gráfica:
Podemos anotar el nombre de la inecuación encabezando la entrada, seguido de los dos puntos.
- Inecuaciones de polinomios en una variable, como x³ > x o y² > y
- Inecuaciones cuadráticas en dos variables, como x² + y² + x y ≤ 4
- Inecuaciones lineales en una variable, como 2x > sin(y) o y < sqrt(x)
Se pueden usar los signos de desigualdad <, >, ≤ y ≥. También puede usarse la notación <= y >= al introducir las expresiones.
Para determinar si un número x0 [o y0] cumple la inecuación s en x [o y], escribimos s(x0) [o s(y0)] en el Campo de Entrada. Para ver si un par de números número x0 e y0 cumplen la inecuación s en x e y, escribimos s(x0, y0). En este caso, si A es el punto (x0, y0), también se admite la sintaxis s(A). En todos estos casos, el resultado será una constante lógica (true o false).
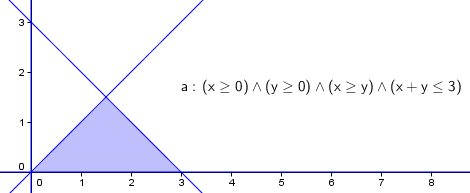
Podemos usar las operaciones lógicas de conjunción y disyunción para representar regiones determinadas por varias inecuaciones simultáneas (programación lineal):
- x > 0 && y >0 && x >y && x+y <3 representa gráficamente la región factible que determinan esas restricciones.
Las herramientas
Punto en Objeto y
Adosa/Libera Punto, así como el comando PuntoEn, nos permite colocar un punto en esta región.