MÓDULO 11

► 11. Conexiones matemáticas

► 11.5 Radiofaros

Objetivos

El dinamismo propio de los fenómenos físicos puede ser aprovechado para la introducción "dinámica" de conceptos matemáticos, a la vez que, gracias a GeoGebra, podemos simular visualmente el movimiento característico del fenómeno.

En este ejemplo mostraremos cómo la medición de una diferencia de tiempo, en microsegundos, en la recepción de dos señales enviadas simultáneamente (en distinta frecuencia) nos permite conocer el lugar geométrico sobre el que se encuentra nuestra posición. Puede ser una excelente introducción a una de las propiedades fundamentales de la hipérbola. De hecho, a la navegación (marítima o aérea) mediante este sistema de localización basado en la emisión de señales simultáneas se le conoce como navegación hiperbólica .

Herramientas y comandos

Usaremos los comandos Distancia, Máximo y Mínimo junto con las siguientes herramientas.

Punto	Segmento	Circunferencia
Hipérbola	Deslizador	Texto
Imagen

Construcción paso a paso

Antes de empezar, puede ser buena idea echar un vistazo al "Ejemplo de construcción" que se encuentra en esta página. Incluso podemos ayudarnos de la Barra de Navegación para realizar un rápido recorrido por los pasos.

Primero prepararemos el escenario.

Preparación

No

No

Desactiva

Distribuimos los elementos y realizamos la construcción.

Etapa 1

Copiar la siguiente imagen al portapapeles (clic derecho, "Copiar").

Herramienta Imagen. Pegamos la imagen con Alt clic, le asignamos 50% de opacidad y la establecemos como fondo.
Herramienta Deslizador. Creamos el parámetro t entre 0 y 20, con incremento de paso 0.01 y ancho 50.
Herramienta Punto. Colocamos un punto (A) sobre zona marítima de la imagen grande y los puntos D y S sobre los radiofaros de Donostia y Santander, respectivamente (sus posiciones están marcadas en la imagen con un punto rojo en la costa, a la derecha Donostia, algo más al centro Santander). Al punto D le ponemos como subtítulo (en propiedades) el nombre Donostia, y al punto S el nombre Santander. Mostramos los rótulos como subtítulos.
Entrada: c = abs(Distancia[A, S] - Distancia[A, D]) / 2
Herramienta Hipérbola. Trazamos la hipérbola con focos S, D y longitud del primer eje c.
Herramienta Punto. Colocamos un punto (B) en la hipérbola.
Copiar la siguiente imagen al portapapeles.

Herramienta Imagen. Pegamos la imagen y le asignamos la posición (esquina1) A - (1, 0.4)

Si el fondo no se muestra transparente, copiar previamente la imagen en el disco duro y escogerla haciendo clic con la herramienta Imagen en una zona vacía de la vista gráfica.

Herramienta Segmento. Creamos los segmentos AS (a), AD (a'), BS (b), BD (b') y DS.
Entrada: f = abs(Distancia[B, S] - Distancia[B, D]) / 2
Herramienta Circunferencia. Trazamos las circunferencias de radio t con centros D y S.

Incorporamos los textos informativos.

Etapa 2

Herramienta Texto. Introducimos los siguientes textos (mixtos, estáticos y dinámicos):

Diferencia = 2c

a = a
a' = a'
Diferencia = 2f
b = b
b' = b'
BIP en la posición A + (-1.3, 0) con la condición de visibilidad t ≥ a

BIP en la posición B + (-0.8, 0) con la condición de visibilidad t ≥ b
BOP en la posición A + (1, 0) con la condición de visibilidad t ≥ a'

BOP en la posición B + (0.3, 0) con la condición de visibilidad t ≥ b'
Mínimo[t, Máximo[a, a']] - Mínimo[a, a'] y condición t ≥ a || t ≥ a'
Mínimo[t, Máximo[b, b']] - Mínimo[b, b'] y condición t ≥ b || t ≥ b'

Colocamos los dos últimos textos a la derecha de las diferencias y mejoramos el estilo de los objetos.

Finalmente, animamos el deslizador t.

Ejemplo de construcción

Radiofaros

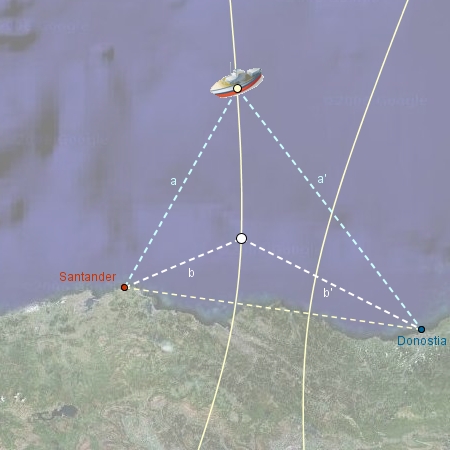
Un receptor en el barco capta señales periódicas y SINCRONIZADAS procedentes de los radiofaros de Santander y Donostia. La diferencia de tiempo en recibir cada señal lo sitúa en una hipérbola de todos los puntos que tienen esa misma propiedad (es decir, en todos esos puntos la diferencia de tiempo o de distancia a los radiofaros es la misma: comprobarlo moviendo el punto blanco). Observar que cuando la diferencia es cero, el barco se sitúa en la mediatriz del segmento Santander-Donostia.

Clic en esta imagen abre la construcción de GeoGebra

Navegación hiperbólica

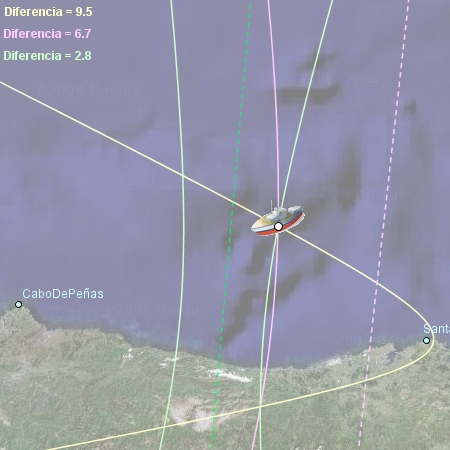
El barco recibe señales SINCRONIZADAS procedentes de tres radiofaros (Cabo de Peñas, Santander y Donostia). La diferencia de tiempo entre cada par de señales lo sitúa en una hipérbola. La intersección de estas hipérbolas determina la posición del barco. (La mayoría de veces, bastan dos hipérbolas; la tercera se comprueba en casos dudosos.)

Clic en esta imagen abre la construcción de GeoGebra

Propuesta de construcción

Realizar una construcción similar a "Radiofaros" con otra imagen costera, colocando dos radiofaros (reales o imaginarios) en ella.

Comentarios

En "Navegación hiperbólica" hemos añadido un tercer radiofaro, gracias al cual podemos determinar la posición exacta del barco. Todas las emisiones están sincronizadas, algo fundamental para el funcionamiento del sistema. Desde el barco se puede medir la diferencia de tiempo entre la recepción de la señal procedente de un radiofaro y de otro y traducirlo a diferencia de distancia. La curva de los puntos cuya diferencia de distancia a dos puntos permanece invariante es una hipérbola, así que tres radiofaros -Cabo de Peñas, Santander y Donostia- generan tres hipérbolas, pues cada par genera una. Allí donde se corten estas hipérbolas estará el barco. En la imagen anterior, las líneas discontinuas corresponden a los puntos equidistantes de cada par de radiofaros (mediatrices).

Investigación:

Todos los sistemas de localización usan conceptos y procedimientos matemáticos. El más conocido actualmente es el sistema GPS. El GPS es un sistema de localización basado en un receptor que usa el tiempo que tarda en llegar las señales procedentes de como mínimo tres satélites (cuatro si se desea precisión) para determinar la posición que ocupa en el espacio (latitud, longitud y altura). Investigar la base matemática de su funcionamiento.