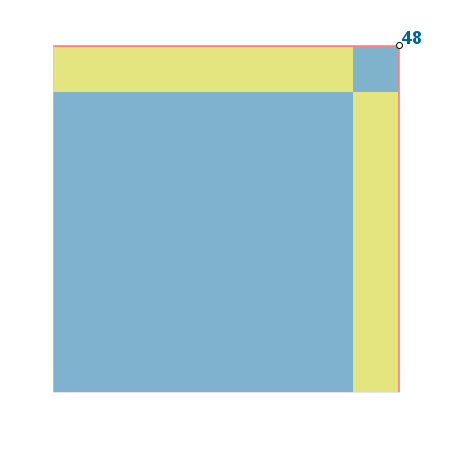|
|
► 11. Conexiones matemáticas
► 11.+ Otros modelos
Otros ejemplos para observar y analizar
|
Mover el punto blanco (con el número azul) hasta el número entero deseado como radicando. Con ayuda de la escala, se puede elegir cualquier entero entre 0 y casi 100 millones. El número corresponde al área del cuadrado de lados grises. El vértice opuesto al punto blanco lo tomamos como origen.
Llevar el primer deslizador hasta su extremo derecho. Se creará el mayor cuadrado (azul) de lado entero que se puede encontrar desde el origen hasta el punto blanco tomando como unidad la escala. El vértice opuesto al origen en ese cuadrado azul se tomará como nuevo origen, y la nueva escala será la décima parte de la anterior. Así, se repite el proceso (en teoría, indefinidamente).
También podemos mantener todos los deslizadores en su extremo derecho. En esta posición, al variar el radicando, la calculadora gráfica nos ofrecerá su raíz cuadrada automáticamente.
|
|
Clic en esta imagen abre la construcción de GeoGebra |
|
Versión GeoGebra de este antiguo juguete educativo, que calcula el producto de dos números y el cuadrado de un número. Mover primero el deslizador del número mayor (pata izquierda del mono, deslizador derecho), y después el deslizador del número menor. |
|
Clic en esta imagen abre la construcción de GeoGebra |
|
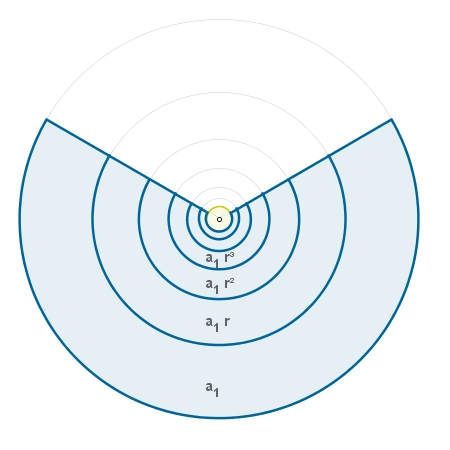
La razón de una progresión geométrica puede entenderse como la constante de una homotecia. Esta asociación permite la visualización de algunos resultados. En este caso, la suma de los infinitos términos de cualquier progresión geométrica decreciente con razón menor que 0.5 y primer término positivo. |
|
Clic en esta imagen abre la construcción de GeoGebra |
|
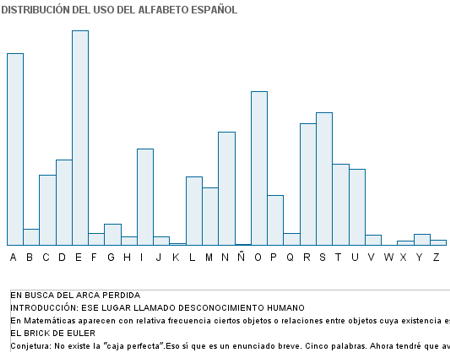
Se ha insertado un texto con el contenido completo de un artículo de varias páginas (previamente, se ha eliminado cualquier formato del texto). Probar a editar el texto y sustituirlo por otro cualquiera.
Sugerencias de actividades a partir de esta construcción estadística:
|
|
Clic en esta imagen abre la construcción de GeoGebra |
|
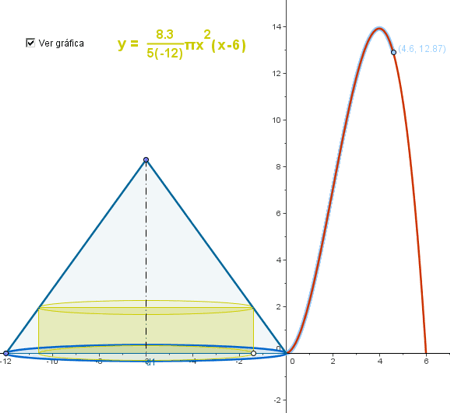
El estudio de la variación de una medida nos permite resolver problemas de optimización. |
|
Clic en esta imagen abre la construcción de GeoGebra |
|
El análisis de la variación de una medida en varios casos concretos puede conducirnos a resultados generales. |
|
Clic en esta imagen abre la construcción de GeoGebra |
|
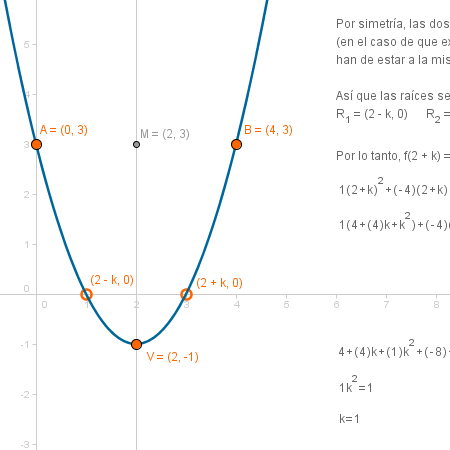
[Comprobación]
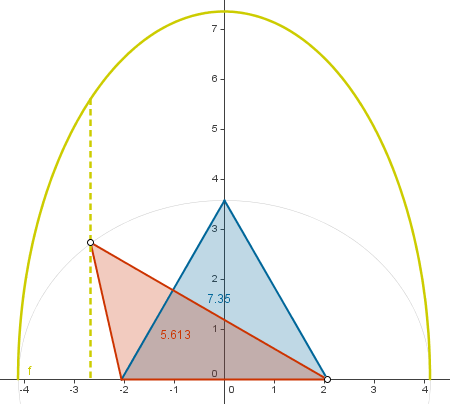
Procedimiento geométrico-funcional para la resolución de una ecuación de segundo grado. |
|
Clic en esta imagen abre la construcción de GeoGebra |
|
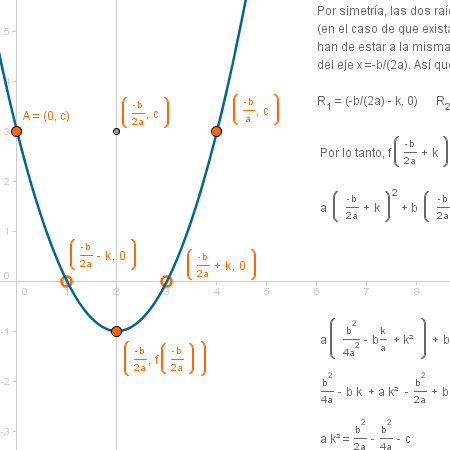
[Demostración]
Obtención de la fórmula de la ecuación de segundo grado por generalización del proceso anterior. |
|
Clic en esta imagen abre la construcción de GeoGebra |