El sonido fundamental no es el único que emite un instrumento al tocar una nota. Simultáneamente, se producen otros sonidos (parciales) de menor intensidad. La distribución e intensidad de estos parciales (timbre) diferencia instrumentos o voces que ejecuten la misma nota.

En el caso de los instrumentos de cuerda y viento, las frecuencias de estos parciales son múltiplos de la frecuencia fundamental F. De estos múltiplos (armónicos), el primero es la propia frecuencia fundamental, el segundo el doble (2F), el tercer armónico el triple (3F), etc.

La cuerda no varía alternativamente entre un armónico y otro, sino que emite todos los sonidos armónicos al mismo tiempo, lo que causó confusión, intriga y discusión entre los matemáticos del siglo XVIII: ¿cómo se las arregla una cuerda para vibrar de varias formas distintas a la vez?

Fourier (con su series ) y Dirichlet (al demostrar su convergencia) resolvieron el problema, abriendo la puerta al análisis armónico. Las series de Fourier representan funciones mucho más generales que las analíticas : el valor de la serie en un entorno no contiene ninguna información sobre el valor en otro entorno.

Resulta, pues, que la cuerda no vibra de ninguno de los modos armónicos, sino de una suma ponderada de ellos. Los coeficientes de la serie de Fourier varían según la intensidad de los distintos armónicos (y por lo tanto, según el timbre del instrumento).

Objetivos

Los guiones no tienen por qué ejecutarse únicamente al hacer clic en un botón o al modificar el valor de una casilla de entrada, sino que cualquier objeto de GeoGebra admite un guión.

En este apartado asociaremos un para de breves guiones a sendas imágenes. Además, usaremos los comandos TocaSonido[TF] y TocaSonido[f, x₁, x₂] para reproducir una función de onda sonora.

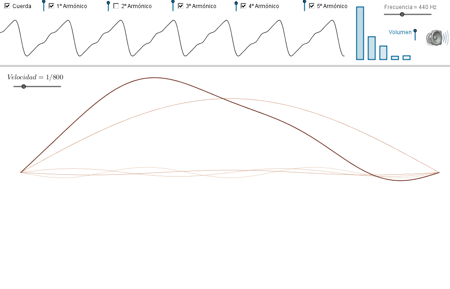
La construcción mostrará tres tipos de información estrechamente relacionados: la gráfica de la función onda, su sonido y el movimiento ralentizado de una cuerda que vibra con la frecuencia elegida.

Pasos de la construcción

Creamos los siguientes deslizadores:

• A1, A2, A3, A4 y A5, entre 0 y 1.5, para recoger las intensidades de los armónicos.
• t, entre 0 y 1000,con paso 0.001, para animar la cuerda vibrante (factor tiempo).
• Frecuencia, entre 100 y 1000 (Hz) (valor inicial, 440 Hz, es la nota "La" de referencia al afinar una orquesta).
• Volumen, entre 0 y 1, para regular el volumen del sonido.
• Velocidad, entre -1000 y -50, con paso 50, para regular la velocidad del movimiento.

Creamos la constante auxiliar k = 2.5, para aumentar la amplitud del movimiento de la cuerda.

Creamos la variable auxiliar v = Frecuencia / (-Velocidad).

Definimos, en el intervalo [-9, 9], las funciones de las ondas estacionarias correspondientes a cada armónico y creamos su suma f(x):

• a1(x) = k A1 sin(π (x/18 + 0.5)) sin(2π t v)
• a2(x) = -k A2/2 sin(2π (x/18 + 1)) sin(4π t v)
• a3(x) = k A3²/6 sin(3π (x/18 + 1.5)) sin(6π t v)
• a4(x) = -k A4⁴/24 sin(4π (x/18 + 2)) sin(8π t v)
• a5(x) = k A5⁵/120 sin(5π (x/18 + 2.5)) sin(10π t v)
• f(x) = a1(x) + a2(x) + a3(x) + a4(x) + a5(x)

Creamos las casillas de control ver1, ver2, ver3, ver4, ver5 y verC para controlar su visualización.

Definimos las funciones correspondientes para la función de onda y su suma (el factor 1/1000 favorece su visualización):

• b1(x) = k A1 sin(Frecuencia/1000 2π x)
• b2(x) = -k A2/2 sin(Frecuencia/1000 4π x)
• b3(x) = k A3²/6 sin(Frecuencia/1000 6π x)
• b4(x) = -k A4⁴/24 sin(Frecuencia/1000 8π x)
• b5(x) = k A5⁵/120 sin(Frecuencia/1000 10π x)
• g(x) = (b1(x) + b2(x) + b3(x) + b4(x) + b5(x))/2.5

Creamos cinco barras para resaltar el valor absoluto de los coeficientes de la serie de Fourier:

• P=(11,-1) (extremo inferior izquierdo del diagrama que vamos a construir).
• pol1 = {Polígono[P, P + (0, 1.5 A1), P + (0.3, 1.5 A1), P + (0.3, 0)]}
• pol2 = {Polígono[P + (0.5, 0), P + (0.5, 1.5 A2/2), P + (0.8, 1.5 A2/2), P + (0.8, 0)]}
• pol3 = {Polígono[P + (1, 0), P + (1, 1.5 A3²/6), P + (1.3, 1.5 A3²/ 6), P + (1.3, 0)]}
• pol4 = {Polígono[P + (1.5, 0), P + (1.5, 1.5 A4⁴/24), P + (1.8, 1.5 A4⁴/24), P + (1.8, 0)]}
• pol5 = {Polígono[P + (2, 0), P + (2, 1.5 A5⁵/120), P + (2.3, 1.5 A5⁵/120), P + (2.3, 0)]}

Insertamos dos imágenes para los altavoces y creamos el valor activado = false para controlar su visiblilidad, introduciendo como condiciones de visibilidad ¬activado y activado, respectivamente:

Guiones GeoGebra

Solo queda asignar un guión a cada imagen.

Imagen  (el factor 1000 neutraliza el factor 1/1000 introducido previamente):

Imagen  :

Ejemplo de construcción

Comentarios

Variando de forma continua el valor de los parámetros, dotamos a las construcciones de movimiento. Así, podemos no solo observar la imagen estática sino el movimiento completo como objeto propio de exploración.

 Investigación:

•  ¿Qué sucede al anular todos los armónicos excepto uno? ¿Cuántos puntos fijos (nodos) aparecen en cada caso?
• Limitando los armónicos a los cinco de la construcción, ¿cuántos puntos de inflexión pueden aparecer como máximo en la función de onda sonora? ¿Y en la cuerda vibrante?
• Busca en Internet más relaciones entre Música y Matemáticas.