MÓDULO 14

Introducción

Inecuaciones

Atracción fractal

Función implícita

Análisis armónico

Otros modelos

 

 


Manual       Imágenes      

 
  • Inicio
  • Módulos
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
    •     

    ► 14. Otros mundos

           ► 14.2 Inecuaciones

    Objetivos

    La versión 4 de GeoGebra incorpora la posibilidad de trabajar con desigualdades e inecuaciones, lo que abre de par en par la puerta a la Programación Lineal.

    Herramientas y comandos

    Usaremos las siguientes herramientas. Las inecuaciones las introduciremos directamente como expresiones en el Campo de Entrada.

    Intersección Punto en objeto Recta

    Propuesta de construcción

    Deberemos realizar una construcción que facilite la comprensión y resolución de un problema típico de Programación Lineal (al nivel de 2º de Bachillerato). El enunciado que hemos elegido como propuesta es el siguiente (P.A.U. Madrid, septiembre 2008):

    Se desea invertir una cantidad de dinero menor o igual que 125000 euros, distribuidos entre acciones del tipo A y del tipo B.

     

    Las acciones del tipo A garantizan una ganancia del 10% anual, siendo obligatorio invertir en ellas un mínimo de 30000 euros y un máximo de 81000 euros. Las acciones del tipo B garantizan una ganancia del 5% anual, siendo obligatorio invertir en ellas un mínimo de 25000 euros.

     

    La cantidad invertida en acciones del tipo B no puede superar el triple de la cantidad invertida en acciones del tipo A.

     

    ¿Cuál debe ser la distribución de la inversión para maximizar la ganancia anual? Determínese dicha ganancia máxima.

    Más abajo mostramos un ejemplo de una construcción similar, ya realizada. El enunciado que hemos elegido para ese ejemplo es el siguiente (P.A.U. Madrid, junio 2008):

    Un distribuidor de aceite de oliva compra la materia prima a dos almazaras, A y B. Las almazaras A y B venden el aceite a 2000 y 3000 euros por tonelada, respectivamente.

     

    Cada almazara le vende un mínimo de 2 toneladas y un máximo de 7 y para atender a su demanda, el distribuidor debe comprar en total un mínimo de 6 toneladas. El distribuidor debe comprar como máximo a la almazara A el doble de aceite que a la almazara B.


    ¿Qué cantidad de aceite debe comprar el distribuidor a cada una de las almazaras para obtener el mínimo coste? Determínese dicho coste mínimo.

    Este enunciado debemos plantearlo, es decir, traducirlo a un sistema de inecuaciones y una función objetivo antes de poder emplear GeoGebra:

    x: número de toneladas de aceite de la almazara A
    y: número de toneladas de aceite de la almazara B

    Función objetivo (que debemos minimizar):

    F(x, y) = 2000x + 3000y

    El siguiente conjunto de restricciones representará gráficamente la región factible:

    0 ≤ x   ∧   0 ≤ y   ∧   2 ≤ x ≤ 7   ∧   2 ≤ y ≤7   ∧   6 ≤ x + y   ∧   x ≤ 2y

     Revisión del modelo ya realizado

    • Usamos la Barra de Navegación para ir viendo toda la construcción paso a paso.
    • Observamos la relación de cada nuevo objeto con los anteriores.

    Ahora realizaremos nuestra propia construcción.

     Realización de nuestro propio modelo

    • Procuremos ser ordenados y claros en el proceso constructivo, siguiendo las etapas lógicas de construcción: función objetivo, inecuaciones, rectas de los lados, vértices de la región factible y valores de la función objetivo en cada vértice.
    • Desde el punto de vista didáctico, resulta muy recomendable aprovechar la herramienta Punto en objeto para situar un punto en la región factible y ver cómo varía el valor de la función objetivo según su posición.
    • Nunca debemos olvidar el cuidado de una cierta estética que añada atractivo a la construcción.
    Ejemplo de construcción similar

     Ejemplo de Programación Lineal: las dos almazaras

     

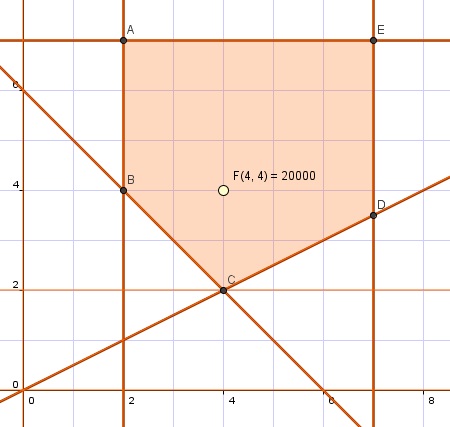
    Una vez construida la región factible con GeoGebra, hayamos sus vértices como puntos de intersección de las rectas que constituyen los lados del recinto. Estos vértices son: A(2,7), B(2,4), C(4,2), D(7,3.5) y E(7,7).

     

    Comparando el valor que alcanza la función objetivo F en cada uno de ellos (25000, 16000, 14000, 24500 y 35000 euros, respectivamente) concluimos que el coste mínimo de 14000 euros se obtiene en el punto C, es decir, adquiriendo 4 toneladas de la almazara A y 2 toneladas de la almazara B.

    Clic en esta imagen abre la construcción de GeoGebra

    Comentarios

    Dependiendo de la experiencia previa con desigualdades, inecuaciones y sistemas, podemos diseñar diferentes actividades ajustadas a esa experiencia.

    Por ejemplo, podemos representar una recta, un semiplano que la tenga como frontera y dos puntos, uno libre y otro restringido a ese semiplano. Moviendo ambos puntos y observando sus coordenadas podemos profundizar en la correspondencia entre la inecuación algebraica y el semiplano correspondiente a su representación gráfica.

    Igualmente, podemos avanzar paulatinamente en puntos restringidos cada vez a más condiciones: un intervalo, un intervalo y un semiplano, tres semiplanos, cuatro semiplanos, etc.

    En cuanto a los vértices de la región factible, al margen del posible ejercicio de resolución del sistema lineal correspondiente para calcular sus coordenadas a mano, podemos usar el punto restringido a la región factible para resaltar el carácter "non plus ultra" de esos vértices.

     Investigación:

    • Explorar las bases lógicas del algoritmo símplex .