TIPOS DE OBJETOS

Introducción

Recorridos

Regiones

Números y ángulos

Valores lógicos

Listas y matrices

Controladores

Textos

Imágenes

MANUAL

 

 

 


Manual       Imágenes      

 
  • Inicio
  • Módulos
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15

    • ► Tipos de objetos

           ► Regiones

     

    Contenido

    1. Introducción
    2. Polígonos
    3. Círculos
    4. Sectores (o arcos)
    5. Cónicas
    6. Intervalos
    7. Inecuaciones
    Introducción

    Algunos de los tipos de objeto con recorrido (y las inecuaciones, que no son recorridos) disponen además de área, es decir, de una región plana asociada.

    Las herramientas  Punto en Objeto y  Adosa/Libera Punto, así como el comando PuntoEn, nos permite colocar puntos en esas regiones.

    Los lugares geométricos pueden rellenarse como si fueran regiones, pero no lo son (no se puede colocar un punto en su sombreado).

    Algunas herramientas y comandos colorean algunas regiones para favorecer la interpretación visual de un resultado. Por ejemplo, la herramienta  Pendiente o el comando IntegralEntre. Pero estos sombreados no son regiones que podamos reutilizar como elementos geométricos, no son objetos, solo son representaciones gráficas.

    Polígonos

    El área de un polígono es una región. El valor del polígono es su medida.

    Las herramientas  Punto en Objeto y  Adosa/Libera Punto, así como el comando PuntoEn, nos permite colocar un punto en esta región.
    Círculos

    El área interior a una circunferencia es una región.

    Las herramientas  Punto en Objeto y  Adosa/Libera Punto, así como el comando PuntoEn, nos permite colocar un punto en esta región.
    Sectores (o arcos)

    El área de un sector es una región. El valor del sector es su medida.

    Las herramientas  Punto en Objeto y  Adosa/Libera Punto, así como el comando PuntoEn, nos permite colocar un punto en esta región.
    Cónicas

    El área de un cónica es una región (su área será considerada indefinida a menos que sea una elipse o una circunferencia).

    Las herramientas  Punto en Objeto y  Adosa/Libera Punto, así como el comando PuntoEn, nos permite colocar un punto en esta región.
    Intervalos

    El área (infinita) de la franja determinada por un intervalo es una región.

    Las herramientas  Punto en Objeto y  Adosa/Libera Punto, así como el comando PuntoEn, nos permite colocar un punto en esta región.

    Inecuaciones

    El área (finita o infinita) determinada por un sistema de inecuaciones es una región.

    Podemos introducir en el Campo de Entrada inecuaciones en una o dos variables (x e y). No hay limitaciones en su representación algebraica, pero solo algunos tipos de inecuaciones pueden aparecer representadas en las vistas gráficas:

    • Inecuaciones de polinomios en una variable, como x³ > x o y² > y
    • Inecuaciones cuadráticas en dos variables (cónicas), como x² + y² + x y ≤ 4
    • Inecuaciones con funciones o funciones recíprocas, como 2x > sin(y) o y < sqrt(x)

    Se pueden usar los signos de desigualdad <, >, ≤ y ≥. También puede usarse la notación <= y >= al introducir las expresiones.

    Para determinar si un número x0 [o y0] cumple la inecuación s en x [o y], escribimos s(x0) [o s(y0)] en el Campo de Entrada. Para ver si un par de números número x0 e y0 cumplen la inecuación s en x e y, escribimos s(x0, y0). En este caso, si A es el punto (x0, y0), también se admite la sintaxis s(A). En todos estos casos, el resultado será una constante lógica (true o false).

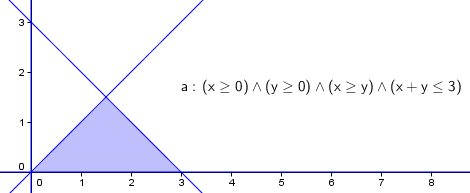
    Podemos usar las operaciones lógicas de conjunción y disyunción para representar regiones determinadas por varias inecuaciones simultáneas (programación lineal):

    • x ≥ 0 && y ≥0 && x ≥y && x+y ≤3 representa gráficamente la región factible que determinan esas restricciones.

    Las herramientas  Punto en Objeto y  Adosa/Libera Punto, así como el comando PuntoEn, nos permiten colocar un punto en esta región.