|
|
► 2. Construcciones ultraligeras
► 2.5 Funciones
Objetivos
El estudio de las familias de funciones es especialmente sencillo con GeoGebra. Basta crear los deslizadores correspondientes a los coeficientes o parámetros que deseamos variar para observar su efecto en la función.
GeoGebra también permite toda clase de operaciones con funciones, incluidas la composición, derivación e integración.
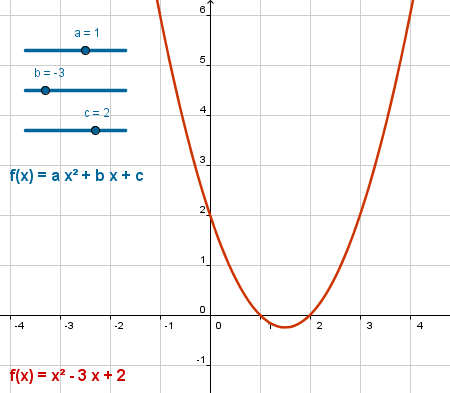
En este ejemplo prepararemos una construcción que facilite la observación del papel que juega cada coeficiente de una cuadrática.
Herramientas y comandos
Veremos la diferencia entre introducir un lugar geométrico e introducir una función. También usaremos las herramientas:
|
|
|
Texto |
Construcción paso a paso
Preparamos el escenario.
|
|
Crearemos la familia de funciones lineales.
|
|
En la expresión anterior, no hay que omitir el espacio entre a y x, y entre b y x, pues tal espacio es el operador de multiplicación. Ver uso de los espacios.
Si hubiéramos introducido la expresión y = a x² + b x + c (como una ecuación en x e y), GeoGebra consideraría a la cuadrática como objeto "parábola" (o "cónica") en vez de como objeto "función". La diferencia entre ambas consideraciones se revela en las distintas acciones que podemos efectuar a través de los comandos (la lista no es exhaustiva):
Comandos de parábola
y = a x² + b x + c
Comandos de función cuadrática
f(x) = a x² + b x + c
Vértices Extremo Tangente Tangente Foco Raíz Directriz Factoriza Parámetro PolinomioTaylor Ejes PuntoInflexión EjePrincipal Simplifica EjeSecundario Desarrolla Angulo Longitud DiámetroConjugado Curvatura Polar VectorCurvatura CírculoOsculador Derivada ListaDeIteración SumaTrapezoidal Integral
|
|
Ejemplo de construcción
Comentarios
Algo similar ocurre con la recta (como lugar geométrico) y la función afín. Si introducimos y = 2x +3, GeoGebra entiende una recta mientras que si introducimos simplemente 2x + 3 se entenderá y nombrará como una función.
![]() Investigación:
Investigación:
- ¿Qué trayectoria describe el vértice de la parábola al variar b? Crear el vértice Extremo[f], activar su rastro y variar b. Comprobar que la trayectoria del vértice sigue la función h(x) = -a x² + c. ¿Por qué?
- ¿Qué sucede con las funciones afines definidas como f(x) = a x + a? ¿Y con las cuadráticas definidas como f(x) = a x² + a x + a? Activar el rastro de cada una de estas funciones antes de variar el valor del deslizador a.
- ¿Cómo es la familia de funciones f(x) = (25 - x²)^(1/n)? (n natural). ¿Converge hacia alguna función al aumentar n?
- Realizar pruebas con los comandos específicos de funciones que aparecen en la tabla anterior. Para conocer la sintaxis de cada uno, basta introducir su nombre en el Campo de Entrada y pulsar F1.