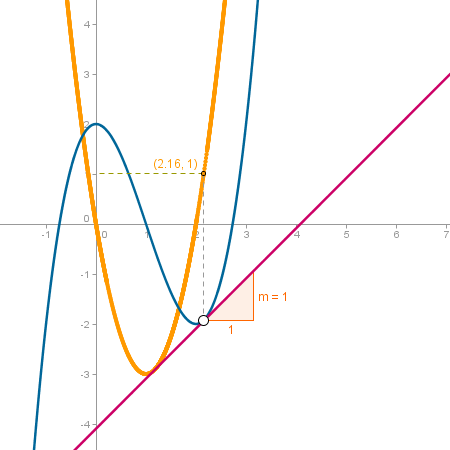MÓDULO 2

Introducción

Geoplanos

Fantasmas

Puntos simétricos

Funciones

Derivada

Otros modelos

 

 


Manual       Imágenes      

 
  • Inicio
  • Módulos
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
    •     

    ► 2. Construcciones ultraligeras

           ► 2.6 Derivada

    Objetivos

    El aprendizaje del estudio local de una función requiere la observación de las variaciones que se producen en cada punto de la gráfica de la función. Al poder colocar un punto móvil sobre cualquier gráfica obtenemos una rápida visualización de lo que sucede para distintos puntos.

    En este ejemplo prepararemos una construcción que facilite la observación de la relación entre la pendiente de la recta tangente a la gráfica de una función en un punto y el valor de la función derivada en ese punto.

    Herramientas y comandos

    Usaremos el comando Segmento y las herramientas:

    Elige y mueve

    		 Punto

    Tangentes

    		 Pendiente
    Construcción paso a paso

    Preparamos el escenario.

     Preparación

    Sí

    No

    Desactiva

    Trazamos la gráfica de la función y la recta tangente en un punto de ella.

     Etapa 1

    • Entrada: x³ - 3x² + 2  (se creará la función f).
    • Herramienta  Punto. Colocamos un punto (A) sobre la gráfica de la función.
    • Herramienta  Tangentes. Trazamos la recta tangente a la gráfica de la función por el punto A.
    • Herramienta  Pendiente. Visualizamos la pendiente (m) de esa recta tangente.
    • Entrada: (x(A), m)  (se creará el punto B).

    Activamos el rastro de B y movemos A. Recordemos que Ctrl+F elimina el rastro.

    Para remarcar todavía más la relación entre A y B, trazamos segmentos de guía y mostramos el rótulo con el valor de B.

     Etapa 2

    • Entrada:

    Segmento[A, B]

    Segmento[B, (0,y(B))]
    Ejemplo de construcción

     Derivada

    Clic en esta imagen abre la construcción de GeoGebra

     Propuesta de construcción

    Realizar una construcción similar para estudiar la función segunda derivada.
    Comentarios

    Si en el proceso anterior queremos impedir que se desplace la función f (por error, al intentar mover el punto A), podemos crear una variable nula, por ejemplo nada=0, y sumarla a la definición de la función:

     x³ - 3x² + 2 + nada

     De esta forma, la función pasa de ser un objeto libre a ser un objeto dependiente y se evita su arrastre accidental. Otra forma es fijar el objeto f, pero tiene el inconveniente de que tenemos que cambiar esta propiedad cada vez que queramos modificar su expresión (los objetos fijos no pueden ser modificados ni eliminados). En este enlace se muestra otro ejemplo de uso de una variable auxiliar nula.

    GeoGebra dispone de varios comandos especializados, incluyendo raíces, derivadas e integrales, que facilitan el análisis de las funciones y curvas paramétricas. Se pueden encontrar en el apartado Funciones de la sección Comandos del manual.

     Investigación:

    • Observar la sintaxis de esos comandos aplicándolos a alguna función concreta y comprobar cómo se visualiza el resultado al usar cada uno de ellos.
    • Modificar en la construcción anterior el valor de f(x) para comprobar el “significado gráfico” de los siguientes resultados:

      La función derivada de una función constante es la función constante cero.

      La derivada de la función identidad es la función constante 1.

      La función derivada de la exponencial es ella misma.