MÓDULO 5

► 5. Deslizadores y animaciones

► 5.6 Cicloides

Objetivos

La geometría se mueve, cobra vida, gracias a los programas de geometría dinámica como GeoGebra. Podemos realizar construcciones cuya manipulación y animación clarifica en gran medida las relaciones geométricas entre los objetos de la escena.

En esta actividad veremos cómo unas pocas instrucciones nos permiten visualizar y manipular las familias de epicicloides, epitrocoides, hipocicloides e hipotrocoides.

Herramientas y comandos

Usaremos las siguientes herramientas.

Punto	Intersección	Segmento
Semirrecta	Lugar	Circunferencia radio
Ángulo	Rota ángulo	Deslizador

Construcción paso a paso

Antes de empezar, puede ser buena idea echar un vistazo al "Ejemplo de construcción" que se encuentra en esta página. Incluso podemos ayudarnos de la Barra de Navegación para realizar un rápido recorrido por los pasos.

Preparamos el escenario.

Preparación

No

No

Desactiva

Creamos rápidamente los parámetros iniciales.

Etapa 1

Entrada:

(4, 0) (se creará el punto A).
A + (1, 0) (se creará el punto B).
3 (se creará el número a).

1 (se creará el número b).

1 (se creará el número c).

k = a/b

Mostramos los deslizadores a, b y c que acabamos de crear. Fijamos sus intervalos respectivos en [0, 6], [-3, 3] y [0, 6].

Con ayuda de las herramientas, podemos construir rápidamente el resto.

Etapa 2

Herramienta Circunferencia radio. Trazamos la circunferencia (d) de centro A y radio a.
Herramienta Circunferencia radio. Trazamos la circunferencia con centro A y radio a + b.
Herramienta Punto. Colocamos un punto (C) en la circunferencia anterior.
Herramienta Ángulo. Creamos el ángulo (α) entre B, A y C (en este orden).
Herramienta Semirrecta. Semirrecta de origen A que pasa por C.
Herramienta Circunferencia radio. Circunferencia de centro A y radio a + b + c.
Herramienta Intersección. Punto de intersección (D) de los dos objetos anteriores (semirrecta y circunferencia).
Herramienta Circunferencia radio. Circunferencia de centro C y radio abs(b).
Herramienta Rota ángulo. Rota D alrededor de C el ángulo k α .
Herramienta Segmento. Segmento entre C y D'.
Herramienta Lugar. Lugar geométrico que recorre el punto D' al mover C.

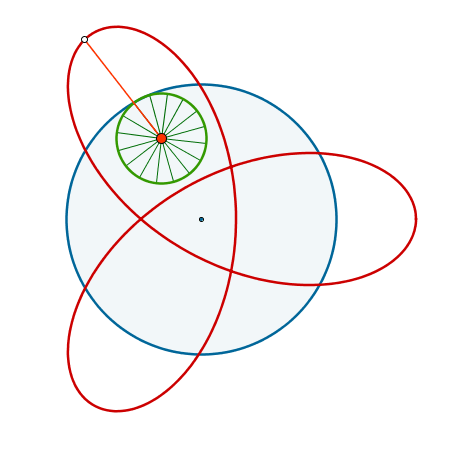
Activamos el rastro de D' y movemos suavemente C, ya sea directamente o seleccionándolo y pulsando las teclas + o -.

Ejemplo de construcción

Epicicloides, epitrocoides, hipocicloides e hipotrocoides

Clic en esta imagen abre la construcción de GeoGebra

Propuesta de construcción

Realizar una construcción similar sobre una recta en vez de sobre una circunferencia, es decir, una construcción que permita visualizar la cicloide y la trocoide.

Comentarios

En la construcción de ejemplo hemos añadido "los radios de la rueda" combinando los comandos Rota, Segmento y Secuencia:

Punto de intersección (E) de la semirrecta y la circunferencia d.
Secuencia[Segmento[C, Rota[E, k α + s pi, C]], s, 0, 2, 1/8]

Además, hemos añadido una curva parametrizada que se encarga de "prolongar" el lugar geométrico para valores superiores a 2pi:

Curva[x(A) + (a+b) cos(t) + c cos((k+1)t), y(A) + (a+b) sin(t) + c sin((k+1)t), t, 0, 20pi]

El comando Curva es muy versátil, pero tiene el inconveniente de que consume muchos recursos, ralentizando la animación.

Investigación:

¿Qué tipo de movimiento realiza el punto blanco cuando los valores (a, b, c) son del tipo (2k, -k, k)?
¿En qué condiciones la "curva" coincide con el "lugar"?
Una moneda gira alrededor de otra idéntica, sin perder contacto y sin deslizarse. Cuando haya completado una vuelta completa, habrá rotado dos veces en vez de solo una. ¿Por qué? Comprobarlo en la construcción anterior (asignar a=2, b=2, c=2).
Existe una gran diversidad de curvas generadas a partir del movimiento de un punto con ciertas limitaciones. Resulta muy interesante buscar algunas de ellas en Internet y comparar las formas de generarlas. Muchas páginas web también ofrecen parametrizaciones de esas curvas.