MÓDULO 7

► 7. Percepción y medición

► 7.2 Ilusiones ópticas

Objetivos

Se pretende realizar una construcción como modelo del uso de GeoGebra para comparar dos imágenes mediante traslaciones o giros.

Los matemáticos, desde hace miles de años, no nos fiamos excesivamente de la vista. Queremos, necesitamos, comprobar la exactitud de la observación y, si es posible, incluso hallar una explicación razonada en las relaciones de las medidas encontradas.

Las mediciones son necesarias para averiguar distintas características de un objeto, como área, volumen, inclinación, peso, etc. Pero además evitan que nos dejemos engañar por nuestra percepción visual.

A continuación comprobaremos con GeoGebra tres ilusiones ópticas.

Herramientas y comandos

Usaremos las siguientes herramientas y no necesitaremos comandos.

	Punto		Circunferencia radio		Rota ángulo
	Deslizador		Imagen

Construcción 1 paso a paso

Antes de empezar, puede ser buena idea echar un vistazo al "Ejemplo de construcción 1" que se encuentra en esta página. Incluso podemos ayudarnos de la Barra de Navegación para realizar un rápido recorrido por los pasos.

Primero prepararemos el escenario.

Preparación

No

No

Automático

Ahora construiremos la primera ilusión.

Etapa 1

Con la herramienta Imagen, pegamos (Alt clic) las dos siguientes imágenes después de copiar cada una al portapapeles (clic derecho, "Copiar"):

Si el fondo no se muestra transparente, copiar previamente las imágenes en el disco duro y escogerlas haciendo clic con la herramienta Imagen en una zona vacía de la vista gráfica.

Con la herramienta Deslizador, creamos un deslizador angular (α) que varíe entre 0° y 74°. Situarlo en 74°.
Con la herramienta Punto, creamos un punto A.
Con la herramienta Rota ángulo, rotamos la mesa verde alrededor del punto A el ángulo α.
Hacemos coincidir la mesa amarilla con la verde.
Opcionalmente, podemos crear circunferencias y arcos que remarquen el recorrido de la mesa.

Ejemplo de construcción 1

Perspectiva

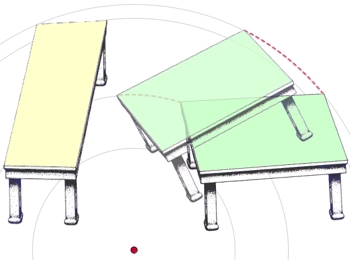
En la construcción las superficies amarilla y verde de las mesas son congruentes: tienen la misma forma y dimensiones. Sin embargo, percibimos la superficie amarilla como “menos ancha y más larga” que la verde. Una rotación dinámica nos puede sacar de nuestro error.

Clic en esta imagen abre la construcción de GeoGebra

Construcción 2 paso a paso

Construiremos la segunda ilusión.

Etapa 2

Abrimos un archivo nuevo y, si es necesario, mostramos los Ejes.
Con la herramienta Punto, creamos dos puntos (A y B) sobre el eje X.
Con la herramienta Imagen, pegamos la siguiente imagen después de copiarla al portapapeles. En la pestaña Posición elegimos como Esquina 1 el punto A.

Si el fondo no se muestra transparente, copiar previamente la imagen en el disco duro y escogerla haciendo clic con la herramienta Imagen en una zona vacía de la vista gráfica.

Con la herramienta Imagen, insertamos de nuevo la misma imagen, pero en esta ocasión probemos a posicionarla directamente en el punto B, señalándolo con la herramienta justo al principio (en vez de hacer clic sobre una parte vacía de la vista gráfica, hacemos clic sobre el punto B).
Ocultamos los Ejes y en las Propiedades de la vista gráfica elegimos negro como color de fondo.
Arrastramos A o B hasta que las dos imágenes se encuentren una al lado de la otra.

Ejemplo de construcción 2

Efecto banana

En la construcción la imagen de la derecha (sea cual sea, ambas son idénticas) siempre parecerá más pequeña. Se debe a que comparamos la curvatura de los arcos limítrofes con el espacio que las separa, con forma de banana. Asociamos menor curvatura con mayor tamaño.

Clic en esta imagen abre la construcción de GeoGebra

Construcción 3 paso a paso

Construiremos la tercera ilusión. En ella, insertaremos y posicionaremos una imagen de 277 píxeles de ancho. Como cada unidad de los ejes cartesianos equivale a 50 píxeles (en la vista estándar), el radio que usaremos para rotar la imagen lo fijaremos en 277/50 unidades.

Etapa 3

Abrimos un archivo nuevo y, si es necesario, ocultamos los Ejes.
Con la herramienta Circunferencia radio, creamos una circunferencia de centro A de radio 277/50.
Con la herramienta Punto, colocamos un punto B sobre esa circunferencia.
Con la herramienta Imagen, pegamos la siguiente imagen después de copiarla al portapapeles, señalando el punto A al hacer clic con la herramienta.

Si el fondo no se muestra transparente, copiar previamente la imagen en el disco duro y escogerla haciendo clic con la herramienta Imagen en una zona vacía de la vista gráfica.

Abrimos las Propiedades de la imagen y en la pestaña Posición asignamos como Esquina 2 el punto B.
Ocultamos A y la circunferencia.
Giremos B y observemos el efecto cóncavo/convexo. Cuando B ocupe la esquina inferior derecha, nos parecerá ver 16 hoyos. Cuando B ocupe la esquina superior izquierda, nos parecerá que el número de hoyos se ha triplicado.

Ejemplo de construcción 3

Iluminación

Al girar la imagen media vuelta, lo que interpretamos como hoyos parecen transformarse en salientes, y viceversa. Se debe a que interpretamos las partes más oscuras como sombras originadas por una luz procedente de la parte superior de la imagen, que es la orientación más habitual en nuestra experiencia.

Clic en esta imagen abre la construcción de GeoGebra

Propuesta de construcción

Realizar una construcción similar que haga girar un cuadrado azul por debajo de otros cuatro cuadrados rojos (asignarles capa 1 en propiedades avanzadas de objeto) al hacer girar un punto sobre una circunferencia (ambos, punto y circunferencia, en capa 2).

Como puede apreciarse (es decir, como "parece percibirse"), el cuadrado azul de la figura de la derecha parece mayor que el de la izquierda, cuando simplemente es el mismo cuadrado rotado. La causa reside en que valoramos las dimensiones del cuadrado azul por el mayor "ancho" visible, así que a medida que los vértices se acercan a la parte visible el ancho parece aumentar hasta alcanzar el tamaño de la diagonal.

Comentarios

Muchas ilusiones ópticas se basan en ciertos mecanismos compensatorios que el cerebro realiza automáticamente a la hora de evaluar una imagen. No es que nuestra mente no se adapte bien al entorno, se trata más bien de todo lo contrario. De hecho, se adapta tan bien a la mayoría de las situaciones que, para no errar en la estimación, redimensiona o sobrevalora ciertos aspectos. La experiencia (la evolución, la supervivencia en definitiva) ha demostrado que tales procedimientos de compensación son útiles y eficaces en la mayoría de las situaciones. Un ejemplo evidente lo encontramos en la "constancia del tamaño", es decir, en nuestra percepción de que apenas varía el tamaño de un objeto al acercarnos o alejarnos de él, a pesar de que el tamaño de su imagen en nuestra retina varía considerablemente.

Sin embargo, si se diseñan cuidadosamente algunas imágenes para provocar la aparición indebida de esos mecanismos de compensación, conseguimos que nuestra propia mente nos engañe. Decimos que estamos ante una ilusión óptica.

Investigación:

Buscar más ilusiones ópticas en Internet y estimar cuáles de las que tienen relación con algún concepto matemático serían susceptibles de ser fácilmente construidas con GeoGebra.