Fermat

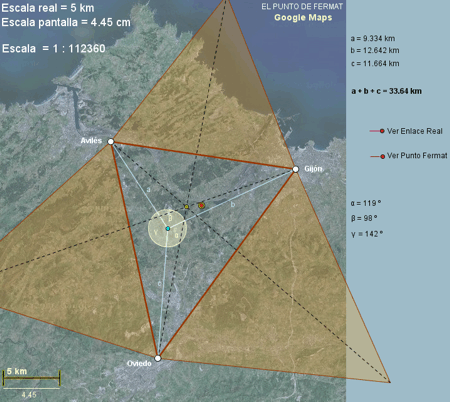
En este ejemplo se desean interconectar tres ciudades mediante una autopista de forma que la longitud total sea mínima, para ahorrar costes. La solución teórica se conoce como punto de Fermat.

Normalmente, las restricciones impuestas por la presencia de poblaciones, accidentes geográficos y naturaleza del terreno, no permiten situar el enlace de las vías en la posición exacta del punto de Fermat. Pero podemos apreciar en la imagen que la solución teórica, en donde los ángulos que forman las semirrectas hacia las ciudades son iguales, no se aleja mucho de la elegida por los ingenieros.

Clic en esta imagen abre la construcción de GeoGebra

 Horizonte

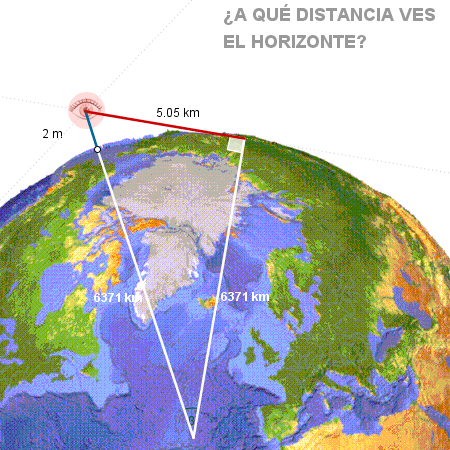
A veces las dimensiones de los objetos implicados no permiten una correcta visualización proporcional, es decir, a escala. Un conocido ejemplo es la representación habitual de los planetas orbitando alrededor del sol. Deberemos entonces sustituir la escala por un esquema.

En la siguiente imagen tenemos un ejemplo. Se desea calcular la distancia entre los ojos de una persona (situados en la imagen a 2 m sobre el nivel del mar) y la línea de horizonte. La elevación de la persona es muy pequeña con relación al radio de la Tierra, así que, con el fin de crear una figura que nos ayude en la resolución del problema, diseñamos la construcción de forma que los objetos no sean proporcionales.

Lo importante es que la mirada del estudiante se dirija hacia dos claves: el ángulo recto que forma la línea de visión con el radio de la tierra en el horizonte y la diferencia de altura con respecto al centro del planeta. El teorema de Pitágoras se encarga del resto.

Clic en esta imagen abre la construcción de GeoGebra

 Efecto Hering

Las rectas paralelas parecen curvarse, debido a la variación angular que experimentan con el haz de rectas concurrentes.

Clic en esta imagen abre la construcción de GeoGebra

 London Eye

La posibilidad de introducir en escena cualquier imagen, ya sea para emplearla como fondo sobre la que trabajar como para usarla como un objeto geométrico más, permite aumentar tanto la calidad estética como el atractivo de algunas construcciones.

En la siguiente figura se ve el resultado de aplicar una homotecia a una imagen. Observemos las tangentes comunes a las circunferencias correspondientes al London Eye. El centro y los radios de la noria también están construidos con GeoGebra.

Clic en esta imagen abre la construcción de GeoGebra

 H (Principio de Huygens )

Cada punto de un frente de onda puede considerarse como nueva fuente de ondas. Estas ondas se extienden en todas direcciones con la misma velocidad, frecuencia y longitud de onda que el frente original.

Clic en esta imagen abre la construcción de GeoGebra

 Burberry's

Repetir una imagen patrón es muy sencillo con el comando Secuencia de GeoGebra.

Clic en esta imagen abre la construcción de GeoGebra