MÓDULO 7

► 7. Percepción y medición

► 7.3 Corona

Objetivos

Nos valdremos de GeoGebra para plantear un problema de forma muy rápida. La visualización dinámica junto con las herramientas de GeoGebra podrán ayudar a los alumnos a resolverlo.

El enunciado es:

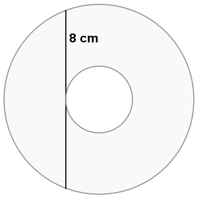
Averiguar el área de la corona circular de la siguiente figura.

Herramientas y comandos

Solo usaremos las siguientes herramientas.

	Punto		Segmento		Circunferencia
	Circunferencia radio		Deslizador		Texto

Construcción paso a paso

Antes de empezar, puede ser buena idea echar un vistazo al "Ejemplo de construcción" que se encuentra en esta página. Incluso podemos ayudarnos de la Barra de Navegación para realizar un rápido recorrido por los pasos.

Primero prepararemos el escenario.

Preparación

Sí

Sí

Fijado

Creamos la figura correspondiente al problema.

Etapa 1

Herramienta Punto. Colocamos los puntos (0,-4) y (0, 4).
Herramienta Segmento. Unimos los puntos anteriores.
Herramienta Deslizador. Creamos un parámetro r entre 0.001 y 8, con incremento 0.01.
Entrada: (r, 0)
Herramienta Circunferencia radio. Trazamos dos circunferencias con centro C y radio r. A una le damos 100% de opacidad y color blanco. A la otra, si es preciso para su visualización, le asignamos una capa superior (p.e. la capa 1, en propiedades avanzadas).
Herramienta Circunferencia. Trazamos la circunferencia con centro C que pasa por A.
Herramienta Texto. Introducimos el siguiente texto mixto:

Área de la corona = Area[e] - Area[c] = Area[e] - Area[c]

Finalmente, adecuamos el Estilo a nuestro gusto.

Ejemplo de construcción

Corona

Clic en esta imagen abre la construcción de GeoGebra

Propuesta de construcción

Realizar otra construcción cualquiera en donde el área de un recinto variable permanezca constante (por ejemplo, el área del rectángulo de vértices opuestos (0,0) y (x, f(x)), bajo la rama hiperbólica f(x) = k/x).

Comentarios

Tanto las posibilidades dinámicas (variaciones de posición y tamaño) como las distintas herramientas disponibles ayudan primero a explorar el problema, buscando relaciones entre los distintos elementos, y posteriormente a ensayar y comprobar las ideas que vayan surgiendo.

Por otra parte, la observación de que variaciones de una dimensión (la longitud) permiten sin embargo la constancia de otras (el área) refuerza la distinción entre los conceptos de ambas magnitudes.

La herramienta Área permite averiguar el área de cada círculo y establecer su diferencia, pudiendo observarse su invariabilidad.

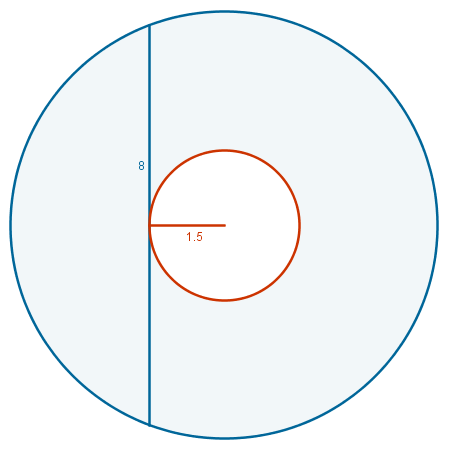
También se puede completar el triángulo rectángulo de catetos los radios y aplicar el teorema de Pitágoras para deducir que la diferencia de los cuadrados de los radios permanece constante (4² = 16 u.c.), y por lo tanto el área de la corona también.

Una vez constatada la independencia del área de la corona respecto al radio del círculo interior, la respuesta surge fácilmente al hacer este radio igual a cero.

Investigación:

Enunciar una versión tridimensional del mismo problema.