|
|
► 8. Subconstrucciones
► 8.4 Periodicidad
Objetivos
Construiremos un mosaico semirregular, creando previamente una herramienta personal que nos permita insertar el patrón generador por traslación, sin tener que construirlo en cada nueva ampliación.
Herramientas y comandos
No se determinan. Existen múltiples formas de construir un cuadrado y un octógono regular inscrito, por lo que la determinación de las herramientas a emplear podría conducir en exceso el método a seguir. Lo dejamos, pues, abierto.
No obstante, para facilitar la colocación de las piezas, debemos partir de dos vértices contiguos del cuadrado, no de dos vértices contiguos del octógono regular (lo que simplificaría la construcción, pero no el uso).
Construcción paso a paso
Primero guardamos en un lugar localizable del disco duro la imagen que asignaremos a la nueva herramienta.
|
|
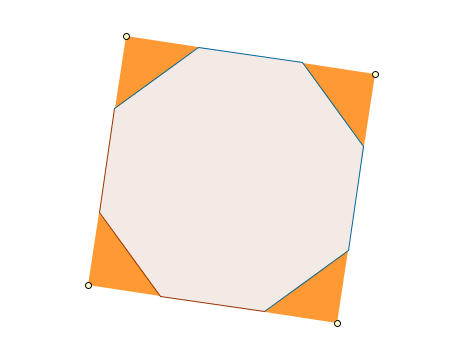
Creamos el patrón.
|
|
Ahora crearemos la nueva herramienta.
|
|
Podemos probar la nueva herramienta haciendo un par de clics en la vista gráfica (o pulsando sobre dos puntos ya existentes).
Guardaremos la nueva herramienta como un archivo GGT, para poder usarla en cualquier construcción:
|
|
Ahora probaremos a abrir la herramienta "patron.ggt" desde cualquier otra construcción.
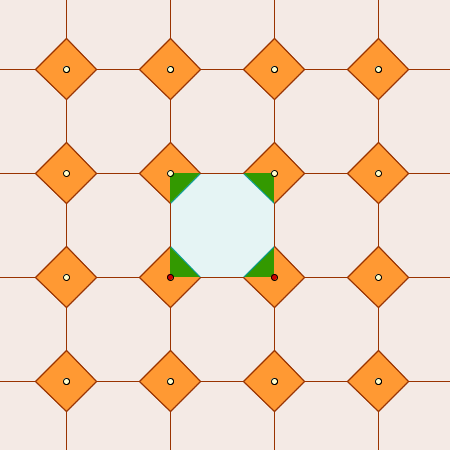
Por último, usamos la herramienta para crear el teselado.
Ejemplo de construcción
|
|
|
Realizar una construcción similar que permita generar un mosaico semirregular diferente al 4-8-8, diseñando la tesela. |
Comentarios
Existen 3 teselados regulares (un polígono regular) y 8 semirregulares (dos o más polígonos regulares). Una muestra de cada una se puede ver en el apartado Teselados de la sección Imágenes.
![]() Investigación:
Investigación:
- Además de teselados con polígonos regulares, existen multitud de formas que también teselan el plano, muchas de ellas empleadas para adoquinar pavimentos o decorar murales. Cabe destacar más de una docena de tipos de pentágonos (irregulares, claro) que teselan el plano, así como los polígonos equiláteros (convexos o no), como la cruz griega. Por supuesto, sin olvidarnos de las transformaciones del tipo "quitar y poner" a las que podemos someter los patrones más simples, como el cuadrado, el triángulo equilátero o el hexágono regular, hasta convertirlos en figuras animales o humanas, como hizo Escher (ver Reptiles en "Otros modelos" del módulo 4). Buscar más información en Internet.