|
|
► 15. Proyecto Gauss
► 15.4 Matemáticas
Matemáticas
En general, el conocimiento adquirido adopta una estructura en red, un conjunto de parcelas interconectadas, con fronteras difusas, en vez de una suma de parcelas aisladas y perfiladas.
Una de las características de las Matemáticas es que en ellas esta característica general del conocimiento se hace más patente, prácticamente omnipresente. En cualquier tema y nivel podemos apreciar la fuerte conexión con conceptos y métodos procedentes de otras ramas. Es por ello que muchas construcciones se prestan a una multiplicidad de puntos de vista, o a establecer relaciones con otras.
Detallaremos un ejemplo de cómo podemos aprovechar estas interconexiones para usar un mismo applet con distintos objetivos, es decir, crear otro ítem didáctico a partir del mismo applet.
Por otra parte, además de este tipo de interconexiones matemáticas, también abunda otro tipo de conexiones debidas a la enorme aplicabilidad de las matemáticas, como son las conexiones con la lógica, los juegos, la naturaleza, la música, los mecanismos, la informática, la astronomía, la logística (entendida como organización), la economía, las teorías físicas, la comunicación, etc.
El ítem didáctico original
Usaremos como ejemplo el ítem didáctico "Omnipoliedro" del Proyecto Gauss:
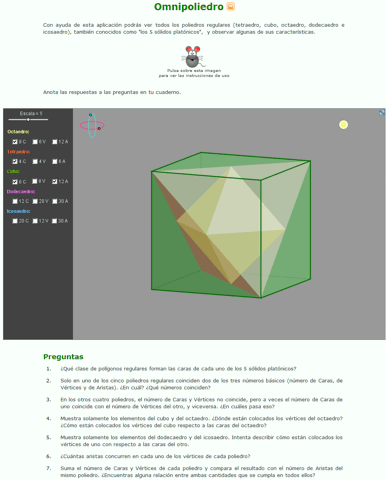
Clic en la imagen para abrir el ítem didáctico
El enunciado de la actividad es:
|
Con ayuda de esta aplicación podrás ver todos los poliedros regulares (tetraedro, cubo, octaedro, dodecaedro e icosaedro), también conocidos como "los 5 sólidos platónicos", y observar algunas de sus características.
Anota las respuestas a las preguntas en tu cuaderno. |
y la batería de preguntas dirigidas elegidas para ese enunciado es:
|
Antes de realizar las siguientes variantes, haremos una pequeña modificación en la página web. Para ello, editamos el archivo HTML y añadimos a la etiqueta <applet> el siguiente parámetro:
<param name= "showAlgebraInput" value= "true" />
Con ello conseguimos que se visualice la Barra de Entrada de GeoGebra.
El nuevo ítem
Enunciado:
|
Con ayuda de esta aplicación podrás ver todos los poliedros regulares (tetraedro, cubo, octaedro, dodecaedro e icosaedro), también conocidos como "los 5 sólidos platónicos", y observar algunas de sus características.
Todos ellos comparten el mismo centro O. Los ocho vértices del cubo tienen por coordenadas O + (±1,±1,±1). Es decir, O+(1,1,1), O+(-1,1,1), O+(1,-1,1), etc.
Usando los vectores de la base canónica i=(1,0,0), j=(0,1,0), k=(0,0,1), esas coordenadas se pueden expresar como O ± i ± j ± k. Es decir, O+i+j+k, O-i+j+k, etc.
Así, por ejemplo, el punto (5,2,3) lo expresaremos como O + 5i + 2j + 3k. |
Preguntas:
|
Propuesta de trabajo
Diseñar un ítem didáctico partiendo de esta versión en inglés
(lo que añade otra conexión) de Geo-GeoGebra
![]() .
.
Comentarios
Muchas situaciones pueden ser analizadas desde distintos puntos de vista y a distintos niveles. Las figuras geométricas pueden servir para realizar las más elementales preguntas, como ¿cuántas esquinas tiene un cuadrado?, hasta las más difíciles, como ¿cuál es el mínimo número de cuadrados, de tamaño variable, que pueden teselar otro cuadrado? (La solución, 21, no aporta gran cosa sobre la forma de construirlo, que dejamos al incansable lector...)
Con frecuencia, el cambio del enunciado y las preguntas solo exige pequeños cambios en el applet, fáciles de llevar a cabo sin necesidad de reconstruirlo por entero.
![]() Investigación:
Investigación:
- Recorre otras construcciones en las páginas "Otros modelos" de cada módulo y analiza si alguno de ellos podría ser de utilidad para otro tipo diferente de actividad.