Construcciones contra dibujos

Las herramientas de GeoGebra no son herramientas de edición gráfica. Las construcciones de GeoGebra no son dibujos. Construir no es lo mismo que dibujar. En una construcción unos elementos se apoyan en otros, de modo que el borrado de una parte puede provocar la eliminación de toda la construcción.

Además, los elementos no se relacionan entre sí por cercanía, ni por tamaño, ni por color. Se relacionan por mantener una dependencia, añadir unas limitaciones.

Sin embargo, las construcciones, consideradas como imágenes, se pueden exportar (Menú Archivo) en formato vectorial para su uso en un editor de gráficos vectoriales. Un punto que hemos colocado con GeoGebra sobre una recta, puede ser desplazado de ella exportando la imagen vectorial y abriéndola con un editor de gráficos vectoriales.

Por otra parte, un dibujo (o cualquier imagen) ajeno a GeoGebra puede servir de modelo a reproducir en forma de construcción, como fondo de la pantalla a modo de planilla, o como un elemento más de la propia construcción, susceptible de ser transformado por diversas operaciones geométricas.

Para más información, ver la sección Módulo 2.4: Imágenes.

Queremos proponer un modelo de actividad como ejemplo de la diferencia existente entre construcción y dibujo.

Para ello, construiremos triángulos con apariencia de triángulos equiláteros. Todos serán iguales a la vista... hasta que se tire de sus vértices. Al hacerlo, revelarán las propiedades geométricas que los distinguen.

Dicho de otra forma, solo uno de ellos deberá ser construido con la condición de mantener sus lados o ángulos siempre iguales entre sí, mientras que los demás serán otros tipos de triángulos más generales que, al mover sus vértices, podrán tomar otras formas además de la equilátera.

Herramientas y comandos

Usaremos las siguientes herramientas.

	Punto		Intersección		Segmento
	Perpendicular		Polígono		Circunferencia

La herramienta fundamental  Elige y mueve la damos por supuesta.

Propuesta de trabajo

Con las herramientas anteriores, proponemos construir en la vista gráfica tres triángulos con estas características:

• Todos deben ser diferentes (equilátero, isósceles, escaleno).
• Todos deben tener la misma apariencia de triángulo equilátero, todos ellos congruentes entre sí. Es decir, aparentemente todos tendrán la misma forma y tamaño. Videoclip

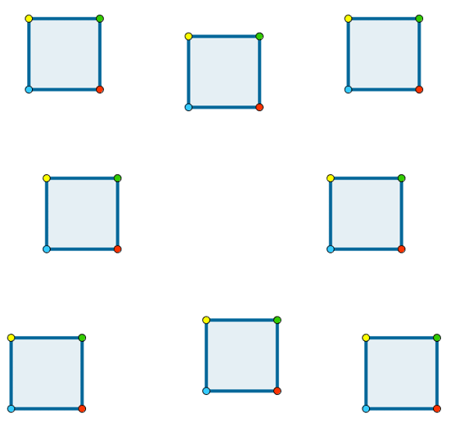
Como construcción de referencia, se puede ver el archivo ocho_cuadrados_A.html, en donde hemos realizado algo similar pero con aspecto de cuadrados en vez de triángulos equiláteros. Hacemos doble clic sobre el applet para abrir la construcción en una nueva ventana. En él hemos construido ocho cuadriláteros donde solo uno de ellos es un cuadrado legítimo y los demás son todos ellos de diferente tipo.

Ahora realizaremos nuestra propia construcción.

Ejemplo de construcción similar

Comentarios

Diferenciar un dibujo de una construcción geométrica requiere cierto entrenamiento, una mirada más abstracta, más inteligente (menos sensorial y más intelectual), sobre lo que vemos. Justamente en esta diferencia reside el contenido matemático que subyace bajo la figura.

La rapidez con la que, gracias a GeoGebra, podemos verificar las variaciones y los invariantes de las figuras al desplazar los puntos que las componen, hace de GeoGebra un excelente recurso para entrar veloz y profundamente en el centro de ese contenido geométrico.

La comprensión que se alcanza mediante esta interacción con las figuras no solo es mucho más rápida que mediante otros métodos sino que además es más permanente y sólida. Lo que a priori era una desventaja (ver con los ojos en vez de con "la mente") se convierte en un aliado ("los ojos" refutan su propia conjetura al observar el comportamiento de la construcción).

 Investigación:

• Resulta interesante proponer formas distintas de construcción de un mismo objeto geométrico, incluso conservando todas las propiedades que le caracterizan (es decir, una verdadera construcción geométrica). En el ejemplo anterior aparece una forma de construir un cuadrado. ¿Conocemos, o podemos descubrir, otras?