Objetivos

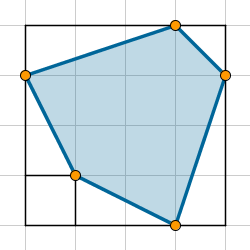
Usaremos GeoGebra para crear rápidamente figuras poligonales con vértices en la Cuadrícula (como si fuera un geoplano). El área de cada una de estas figuras es sencilla de calcular simplemente contando cuántas casillas o fracciones de casillas abarca. No hace falta recurrir a ninguna fórmula, así que es una buena actividad para profundizar en los conceptos de área y unidades de área.

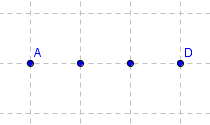
Por otra parte, es habitual la confusión numérica entre número de "intersecciones o puntos de la Cuadrícula" y número de segmentos unidad. Por ejemplo, en la siguiente imagen se aprecia que la separación entre los 4 puntos no es de 4 unidades lineales, sino solo 3:

Se podrán redistribuir los vértices del polígono, así como crear nuevos polígonos.

 Esta actividad es muy flexible en cuanto a la forma de las figuras creadas, por lo que puede ser aprovechada para impulsar la imaginación y creatividad de los alumnos.

Herramientas y comandos

Solo precisaremos de dos herramientas: la herramienta fundamental para mover y seleccionar (herramienta  Elige y mueve) y la herramienta  Polígono. Una vez dibujado un polígono, procederemos a variar su Estilo (grosor de los segmentos, colores, transparencia...) a nuestro gusto.

Practicaremos también los procedimientos para guardar archivos y exportar imágenes, descritos en el Menú Archivo.

 Los botones Deshace y Rehace son muy útiles para devolver la construcción a un estado anterior.

Construcción paso a paso

Primero prepararemos el escenario.

En la Barra de Estilo, desactivamos ver Ejes, activamos ver Cuadrícula y elegimos la tercera opción de atracción a cuadrícula: "Fijado a Cuadrícula".

Ahora construimos una figura poligonal usando la herramienta  Polígono:

• Marcamos varios puntos diferentes y cerramos el polígono volviendo a hacer clic sobre el primer punto marcado.
• Seleccionar la herramienta  Elige y mueve (o pulsar la tecla Esc). Probar a mover el polígono con ayuda de esta herramienta.
• Clic sobre el polígono, sus vértices y sus lados para variar las propiedades de Estilo a gusto, usando la Barra de Estilo de la vista gráfica.

 Podemos hacer clic sobre el objeto en la Vista Gráfica o en la Vista Algebraica. A veces, debido a la cercanía de los objetos geométricos, resulta más cómodo emplear esta última.

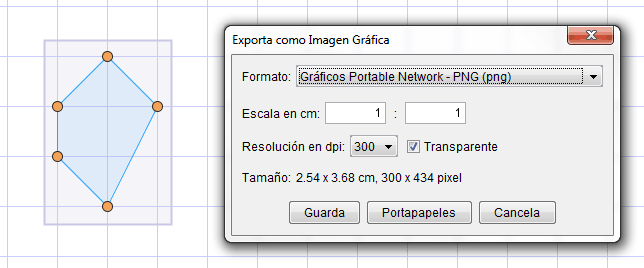
Por último, exportamos la imagen de la figura obtenida:

• Enmarcar la figura arrastrando el ratón y exportar el cuadro enmarcado como imagen PNG usando la opción del Menú Archivo Exporta Vista gráfica como imagen.

• Guardar el archivo a través de Menú Archivo Guarda.

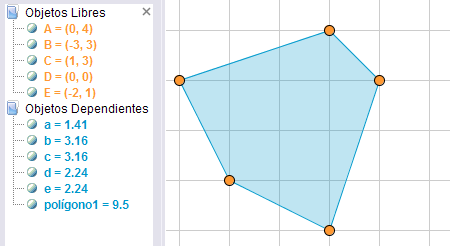
Ejemplo de construcción

Pentágono   Una vez realizada la construcción podemos hacer un volcado de pantalla al portapapeles (tecla Imp Pant), o exportar como imagen la vista gráfica con la cuadrícula visible, para su impresión. La imagen obtenida nos servirá para preguntar sobre el área de su superficie. Basta mover los vértices para obtener rápidamente distintas variantes del mismo problema.

Clic en esta imagen abre la construcción de GeoGebra

Propuesta de trabajo

Realizar una construcción similar que muestre un recinto heptagonal. Deben verse los rótulos de los vértices, pero no los rótulos de los lados ni el rótulo del polígono. Escribir el enunciado de un problema basado en la figura construida.

Comentarios

Una ventaja de usar el soporte dinámico frente al estático es que una sola construcción nos vale para plantear multitud de problemas del mismo tipo, simplemente variando la posición de los vértices.

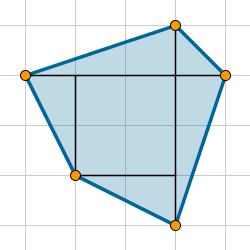
Existen diversos procedimientos para contar las casillas o fracciones de casillas correspondientes al área de la figura. Algunos emplean la disección y adición, cortando y sumando las partes simples resultantes. Otros emplean la sustracción, restando el área de aquellas partes que faltan para obtener un rectángulo.

Merece la pena dedicar tiempo a discutir la eficacia de estos métodos y sus variantes sobre diversas figuras. Un método puede ser muy rápido sobre alguna figura, pero volverse relativamente lento sobre otras. Esto es muy habitual en Matemáticas, de ahí la conveniencia de disponer siempre de varios métodos o formas de enfocar el problema.

A los pocos ensayos, los alumnos se darán cuenta de que el área que buscan aparece en la Vista Algebraica como valor del polígono. Si se quiere impedir esto, basta ocultar la vista algebraica en el applet.

También se puede formular el problema a la inversa: prefijar el valor (entero o mitad de entero) de un área y solicitar el correspondiente ejemplo de polígono (uno cualquiera o con un número prefijado de lados o con alguna propiedad como cierta simetría...).

 Investigación:

• Valorar la dificultad del siguiente problema: "Encontrar todos los triángulos de área 1 que se pueden disponer sobre una cuadrícula de 3x3 unidades." ¿Es tan fácil como parece? ¿Tiene la misma dificultad resolverlo en papel que con GeoGebra?
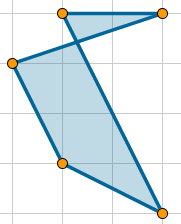
• ¿Qué sucede con los polígonos cruzados (los no simples, aquellos en los que al menos dos lados se intersecan)? ¿Continúa siendo sencillo el cálculo del área? ¿El valor que GeoGebra otorga al polígono sigue correspondiendo al área?