|
|
► 2. Deslizadores y animaciones
► 2.+ Otros modelos
Otros ejemplos para observar y analizar
|
Un ajedrez virtual es un sencillo ejemplo de imágenes móviles sobre una imagen fija. |
|
Clic en la imagen para abrir el applet de GeoGebra |
|
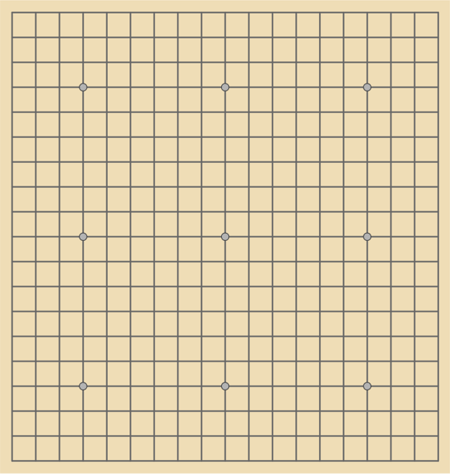
El tablero de Go es una gran cuadrícula que podemos aprovechar para proponer un montón de problemas, ya sean de Go, de Go-moku, de configuración, de medición... |
|
Clic en la imagen para abrir el applet de GeoGebra |
|
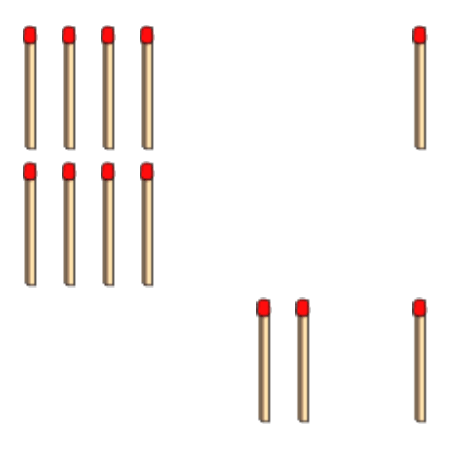
Existe una gran variedad de juegos y rompecabezas basados en la configuración de una colección de objetos: piedras, monedas, palillos, cerillas... Algunos, como el Nim, tienen varios siglos de antigüedad. En este ejemplo, el movimiento de los puntos está limitado a un segmento. |
|
Clic en la imagen para abrir el applet de GeoGebra |
|
Las piezas pueden dejarse libres o bien dirigidas por puntos atraídos a la cuadrícula. |
|
Clic en la imagen para abrir el applet de GeoGebra |
|
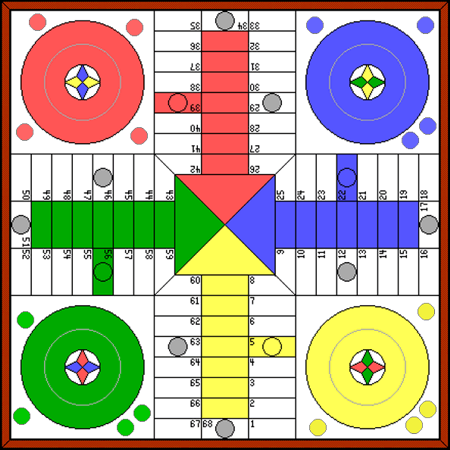
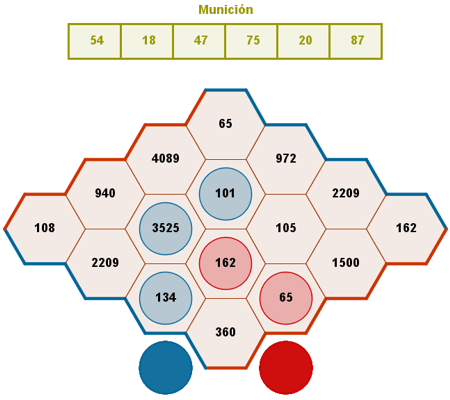
La mayor parte de los juegos de mesa son de estrategia, de azar o ambas cosas combinadas. En cualquier caso, son fuente inagotable de problemas matemáticos (configuraciones, combinatoria, probabilidad, estadística...). |
|
Clic en la imagen para abrir el applet de GeoGebra |
|
Con GeoGebra es fácil diseñar tableros de juego personalizados. Podemos escoger como plantilla una cuadrícula ortogonal o una plantilla isométrica. |
|
Clic en la imagen para abrir el applet de GeoGebra |
|
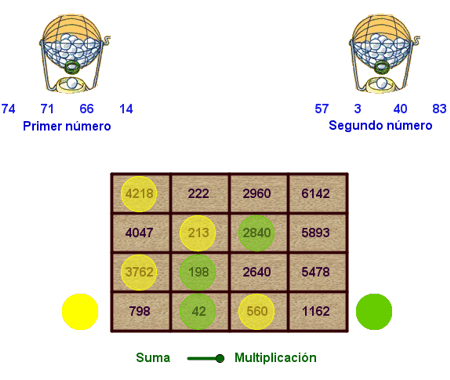
La posibilidad de generar números aleatorios permite crear rápidamente nuevos retos en el mismo escenario. |
|
Clic en la imagen para abrir el applet de GeoGebra |
|
Una ventaja de las construcciones virtuales es que las piezas no se pierden, ni se rompen, ni se tiran... Pero si queremos podemos convertirlas en cartulina simplemente imprimiéndolas. |
|
Clic en la imagen para abrir el applet de GeoGebra |
|
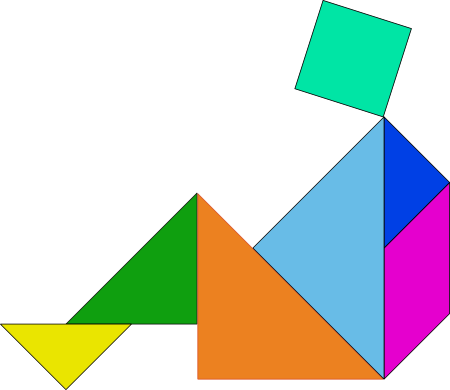
Siete polígonos pueden formar incontables figuras diferentes. |
|
Clic en la imagen para abrir el applet de GeoGebra |
|
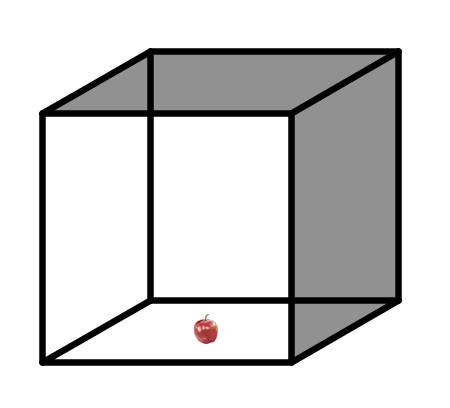
La mirada matemática es la mirada que no se conforma con ver, es la mirada que quiere observar, buscar, explorar, encontrar cualquier tipo de relación entre lo que ya conoce y lo que ve. |
|
Clic en la imagen para abrir el applet de GeoGebra |
|
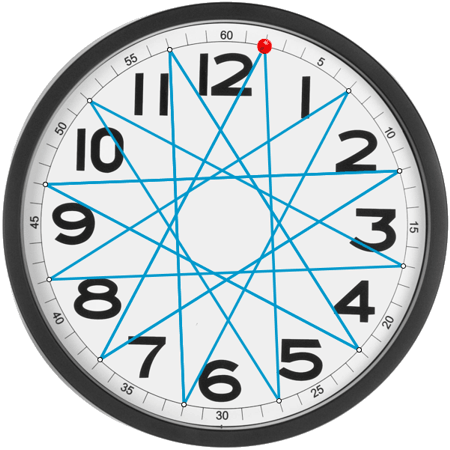
Un reloj analógico permite plantear un sinfín de cuestiones matemáticas. |
|
Clic en la imagen para abrir el applet de GeoGebra |
|
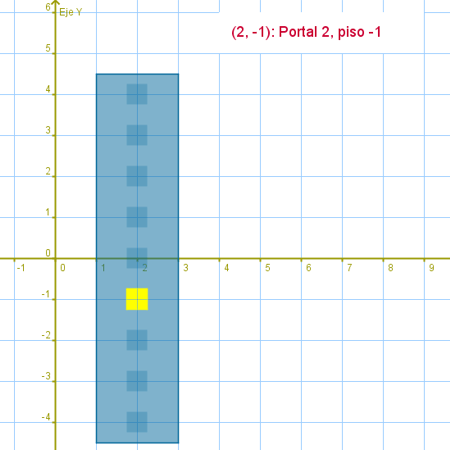
La cuadrícula de GeoGebra es de gran ayuda para realizar rápidamente gráficos acordes a nuestros objetivos. |
|
Clic en la imagen para abrir el applet de GeoGebra |
|
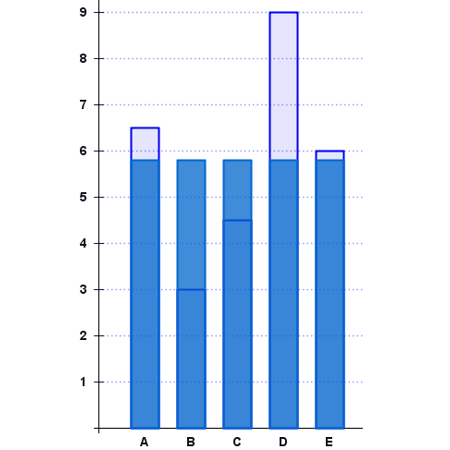
Las imágenes y gráficos cada vez abundan más en la sociedad actual. Su correcta interpretación es fundamental para posibilitar una auténtica libertad en el criterio personal acerca del entorno. |
|
Clic en la imagen para abrir el applet de GeoGebra |
|
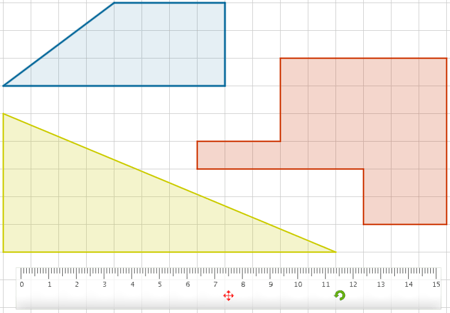
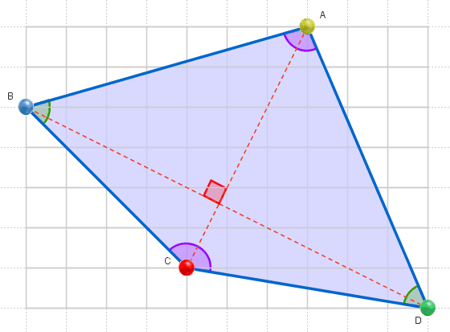
También podemos trazar rápidamente distintas figuras con las que trabajar la medición de longitudes y áreas. |
|
Clic en la imagen para abrir el applet de GeoGebra |
|
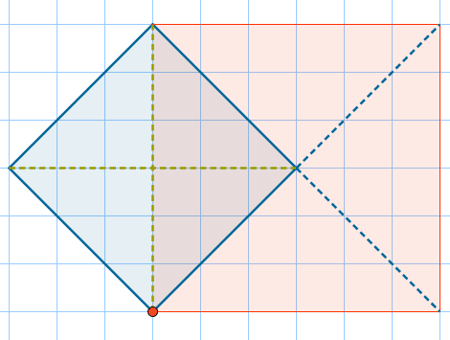
El problema de la relación entre el lado de un cuadrado y su diagonal está lleno de historia y conceptualización. |
|
Clic en la imagen para abrir el applet de GeoGebra |
|
Copiando las imágenes en un editor de texto podemos obtener rápidamente un montón de hojas con gráficos personalizados que sirvan como ejemplos o ejercicios. |
|
Clic en la imagen para abrir el applet de GeoGebra |
|
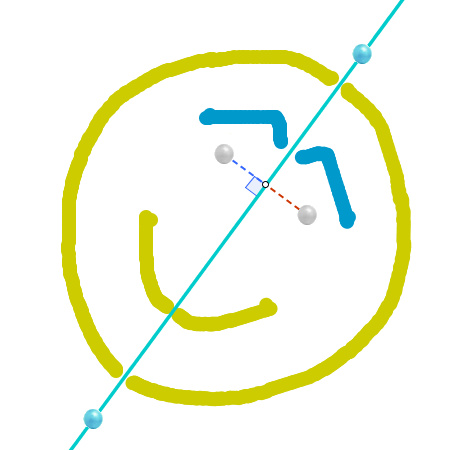
La opción Activa Rastro nos permite convertir los puntos en pinceles. |
|
Clic en la imagen para abrir el applet de GeoGebra |