Bastan muy pocos elementos para crear una escena en la que proponer la observación del comportamiento de los objetos.

Clic en la imagen para abrir el applet de GeoGebra

La ventaja de mostrar pocos elementos es que favorece la concentración de la atención en las relaciones ocultas e invariantes que rigen los movimientos.

Clic en la imagen para abrir el applet de GeoGebra

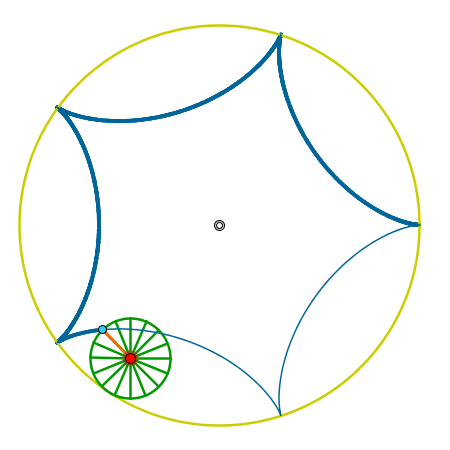
La visualización de los conceptos matemáticos es más mental que física. La ocultación de líneas que dirijan al ojo puede ayudar a ejercitar la sustitución de la imagen física por la imagen mental.

Clic en la imagen para abrir el applet de GeoGebra

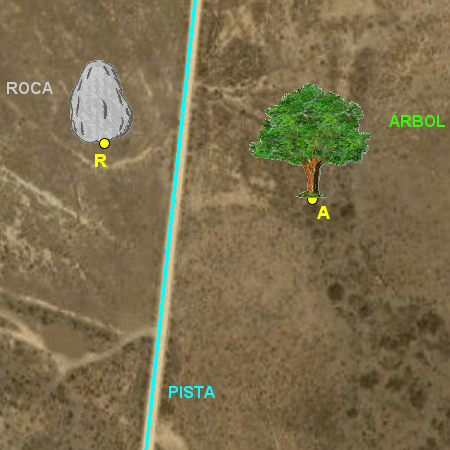
Este tipo de ejercicios de abstracción se puede aplicar a prácticamente a cualquier escenario en donde existan objetos relacionados.

Clic en la imagen para abrir el applet de GeoGebra

Las casillas de control permiten al usuario elegir en cada momento los objetos a visualizar. En este ejemplo se combina el uso de casillas de control, rastro activo y color dinámico para producir el resultado deseado.

Clic en la imagen para abrir el applet de GeoGebra

Las casillas de control, además de permitir visualizar u ocultar objetos a voluntad, también permiten (aparentemente) al usuario variar las propiedades de un objeto. Todo lo que tenemos que hacer es duplicar el objeto, asignarle a la copia otras propiedades y condicionar la aparición de uno u otro a la activación de la casilla de control.

Clic en la imagen para abrir el applet de GeoGebra

El uso del rastro que deja un punto nos permite seguir con facilidad la trayectoria recorrida.

Clic en la imagen para abrir el applet de GeoGebra

Las animaciones ayudan a comprender el comportamiento de cualquier tipo de variación, ya sea en el espacio o en el tiempo.

Clic en la imagen para abrir el applet de GeoGebra

Básicamente existen dos formas, complementarias, de entrenarse en la resolución de problemas: resolver problemas de dificultad progresiva y analizar estrategias de resolución en problemas resueltos. En este (difícil) problema se muestra una combinación de ambas formas.

Clic en la imagen para abrir el applet de GeoGebra

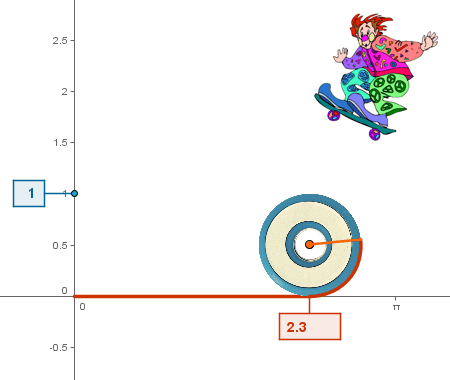
La simulación de la rectificación de una circunferencia de radio variable es una excelente visualización de la relación existente entre el diámetro y la longitud de la circunferencia.

Clic en la imagen para abrir el applet de GeoGebra

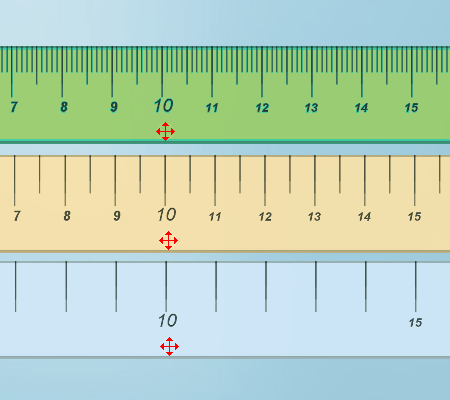
Los propios materiales de construcción y medición son muy válidos como objetos de observación matemática.

Clic en la imagen para abrir el applet de GeoGebra

 Paralelas

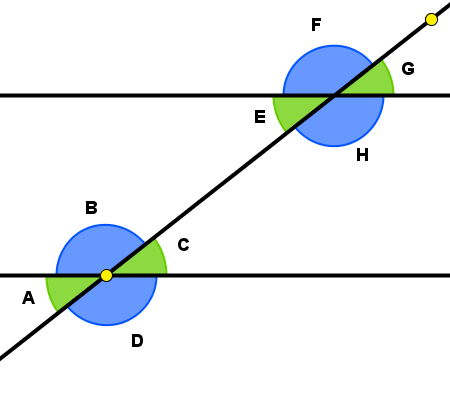
En este ejemplo encontramos una vez más cómo la naturaleza de las relaciones matemáticas se visualiza mucho mejor gracias al dinamismo de los objetos, de forma que rápidamente podemos detectar qué tipo de cosas varían y qué tipo de cosas permanecen invariantes.

Clic en la imagen para abrir el applet de GeoGebra