MÓDULO 14

► 14. Otros mundos

► 14.3 Atracción fractal

Objetivos

Los fractales (como los generados con GeoGebra por Manuel Sada ) son objetos matemáticos recientes y muy atractivos, tanto desde el punto de vista teórico como práctico. Con el nombre de "El juego del caos" (Chaos game o "algoritmo de iteración aleatoria" ) se conoce a un tipo de iteración que, a veces, genera un modelo fractal de forma no recursiva, como atractor de un sistema dinámico caótico .

Se eligen n puntos o vértices y otro punto D cualquiera. En cada paso, y aleatoriamente (con igual probabilidad 1/n), el punto D se dirige hacia uno de los n vértices, recorriendo solo una fracción constante de la distancia que los separa.

En este apartado, veremos cómo usar guiones GeoGebra y guiones JavaScript para generar el triángulo de Sierpinski mediante este proceso iterativo.

Protocolo de construcción

Nombre	Definición	Valor	Subtítulo
Punto A		A = (-1, -2)
Punto B		B = (9, -1)
Punto C		C = (5, 5)
Triángulo tri	Polígono A, B, C	tri = 32
Segmento a	Segmento [A, B] de Triángulo tri	a = 10.05
Segmento b	Segmento [B, C] de Triángulo tri	b = 7.21
Segmento c	Segmento [C, A] de Triángulo tri	c = 9.22
Número r		r = 0
Número v		v = 0
Número z		z= 0
Número m		m = 0
Valor Booleano dV		dV = true
Valor Booleano eV		eV = true
Punto D		D = (3, 0)
Punto D'	D	D' = (3, 0)
Punto E		E = (3, 0)
Segmento d	Segmento [D, E]	d = 0
Segmento e	Segmento [D, 2D - E]	e = 0
Botón botón1		botón1	Una iteración
Botón botón2		botón2	Mil iteraciones
Botón botón3		botón3	Borrar

Construcción paso a paso

Creamos el triángulo ABC (cualquiera). Asignamos a A el color naranja, a B el color azul y a C el color rojo.

Creamos las variables auxiliares r = 0, v = 0, z = 0, m = 0, dV = true y eV = true.

Añadimos los puntos D = (3, 0) y D' = D.

Minimizamos el tamaño del punto D y activamos su rastro. (El punto D' sirve para distinguir claramente su posición.)

Añadimos el punto E = (3, 0) (que ocultamos) y los segmentos d = Segmento [D, E] y e = Segmento [D, 2D - E].

Asignamos a los puntos D y D' y a los segmentos d y e el color dinámico R: r, G: v, B: z.

Asignamos a d y e la condición de visibilidad dV y eV, respectivamente, y a e un estilo discontinuo de trazo.

Finalmente, añadimos tres botones, con los subtítulos que aparecen en el Protocolo.

Guiones GeoGebra

Solo queda asignar un guión (una serie de instrucciones) a cada pulsación de los botones. Usaremos guiones de GeoGebra para los botones 1 y 3, y un guión JavaScript para el botón 2.

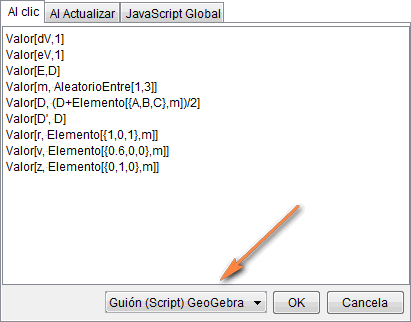
Botón 1, "Una iteración":

Valor[dV,1] asigna a dV el valor 1 (true): el segmento d permanecerá visible.
Valor[eV,1] asigna a eV el valor 1 (true): el segmento e permanecerá visible.
Valor[E,D] asigna a E el valor de D: el punto E será la posición de partida de D.
Valor[m, AleatorioEntre[1,3]] asigna a m un entero aleatorio entre 1 y 3.
Valor[D, (D+Elemento[{A,B,C},m])/2] asigna a D el punto medio entre D y un vértice elegido al azar.
Valor[D', D] asigna a D' el mismo valor que tiene D.
Valor[r, Elemento[{1,0,1},m]] asigna al componente rojo un valor dependiente del vértice elegido.
Valor[v, Elemento[{0.6,0,0},m]] asigna al componente verde un valor dependiente del vértice elegido.
Valor[z, Elemento[{0,1,0},m]] asigna al componente azul un valor dependiente del vértice elegido.

Al acabar, debemos pulsar el botón .

Observemos que se usa el comando Valor en vez del signo =, debido a que, en un guión de GeoGebra, el signo = redefine el objeto, mientras que el comando Valor solo modifica el valor del objeto.

Botón 3, "Borra":

Valor[E,D] asigna a E el valor de D.
ZoomAleja[1] actualiza la vista gráfica, lo que provoca el borrado de los rastros.

Guiones JavaScript

Los guiones de GeoGebra son mucho más sencillos que los guiones JavaScript, pero estos últimos tienen mayor versatilidad y potencia.

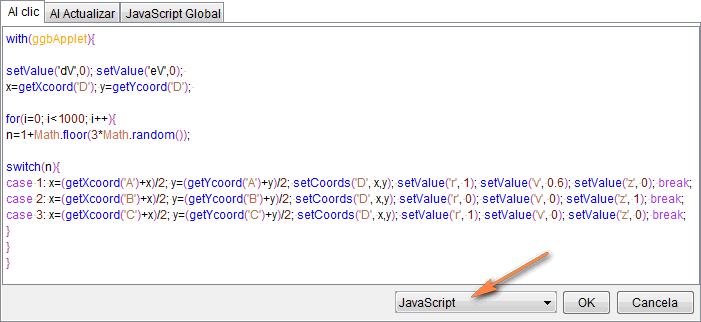
En el botón 2, "Mil iteraciones", se hace uso de los comandos de JavaScript específicos de GeoGebra setValue, getXcoord, getYcoord y setCoords, así como de los comandos generales with, for y switch:

with(ggbApplet){ aplica el prefijo "ggbApplet." a todas las instrucciones siguientes.

setValue('dV',0); setValue('eV',0); asigna el valor 0 a dV y eV (oculta d y v).

x=getXcoord('D'); y=getYcoord('D'); recupera las coordenadas de D (x, y).

for(i=0; i<1000; i++){ Reitera mil veces.

n=1+Math.floor(3*Math.random()); crea un entero aleatorio entre 1 y 3.

switch(n){ según el valor de n, actualiza el valor de D y el color correspondiente.

case 1:

x=(getXcoord('A')+x)/2; y=(getYcoord('A')+y)/2;

setCoords('D', x,y); setValue('r', 1); setValue('v', 0.6); setValue('z', 0); break;

case 2:

x=(getXcoord('B')+x)/2; y=(getYcoord('B')+y)/2;

setCoords('D', x,y); setValue('r', 0); setValue('v', 0); setValue('z', 1); break;

case 3:

x=(getXcoord('C')+x)/2; y=(getYcoord('C')+y)/2;

setCoords('D', x,y); setValue('r', 1); setValue('v', 0); setValue('z', 0); break;

} cierra el switch, es decir, el selector según el valor de n.

} cierra el bucle for que reitera mil veces.

} cierra la instrucción with.

Al acabar, debemos pulsar el botón .

Ejemplo de construcción

Atracción fractal

$Construcción: Atracción fractal$

Clic en esta imagen abre la construcción de GeoGebra

Propuesta de construcción

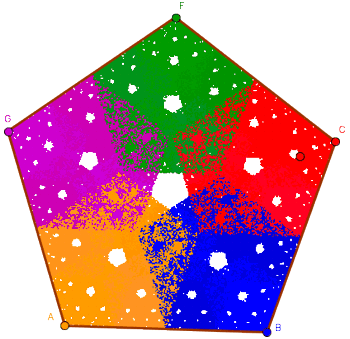
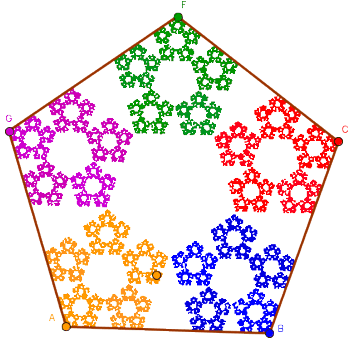
Realizar una construcción similar para cinco vértices y una fracción constante recorrida de 1/2 (imagen izquierda) o de 5/8 (imagen derecha).

El símbolo de multiplicación en JavaScript es el asterisco * (no se admite el espacio).

Comentarios

Los guiones (scripts) abren un sinfín de posibilidades, prácticamente solo limitadas por nuestra imaginación.

El uso de los guiones de GeoGebra no precisa de ninguna experiencia previa con la programación. Por su parte, el uso de guiones JavaScript permite todavía más posibilidades a los que posean nociones básicas de este lenguaje.

Investigación:

Busca en Internet algún manual básico de JavaScript.