MÓDULO 14
Manual
Imágenes
Inicio
  |
► 14. Otros mundos
► 14.4 Función implícita
Objetivos
Queremos hacer uso de las funciones implícitas para visualizar los pares de puntos del plano que cumplen una relación dada. En concreto, esta relación viene dada por el siguiente problema.
|
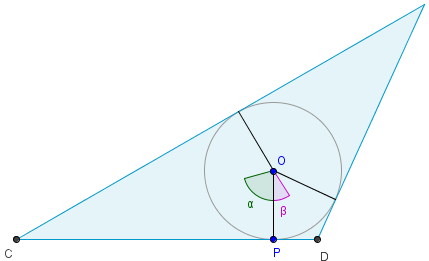
Tomemos el círculo de radio 2 centrado en el origen. Podemos considerar todos los triángulos que lo tienen
como círculo inscrito. Hay una infinitud de tales triángulos, pero no todos de
igual área. Fijemos, pues, un área A. Para evitar repeticiones por rotación,
consideremos que la base CD es horizontal. La cuestión es, ¿qué relación existe entre
todos esos triángulos que tengan la misma área dada?
|
Obsérvese
que, en este contexto, el área coincide con el perímetro.Llamando α (∡POC), β (∡POD) y γ a la mitad de los ángulos centrales, tenemos que:
tan(α) + tan(β) + tan(γ) = A/4
Como γ = π - α - β, llamando x e y a tan(α) y tan(β), respectivamente, tenemos:
x + y + (x+y)/(xy-1) = A/4
Ecuación que quitando denominadores, y tomando k = -A/4, podemos expresar como:
x² y + x y² + k x y = k
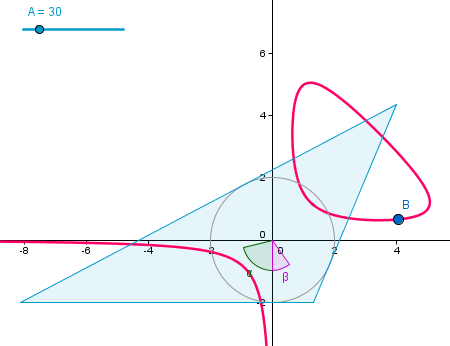
Esta ecuación corresponde a una curva algebraica plana. Para cada valor (x, y) de esta curva (con ambas coordenadas positivas), habrá un triángulo. Y viceversa, cada triángulo determinará un valor x (positivo) correspondiente a uno o dos puntos de la curva.
Ejemplo de construcción
|
La construcción es sencilla y fácil de reproducir. La importante novedad es la gran facilidad con la que podemos crear la curva algebraica. Partiendo del deslizador A (que representa el área fija), introducimos k = -A/4 y, finalmente, la ecuación x² y + x y² + k x y = k. Así de simple. |
|
Clic en esta imagen abre la construcción de GeoGebra |
Curvas
algebraicas planas
|
|
|
Realizar una construcción similar a partir del punto P(0,2) en vez de (0,-2). |
Comentarios
Las funciones implícitas nos permiten explorar relaciones entre dos variables que no admiten una expresión explícita (despejar una en función de la otra). Además, sirven como apoyo en el proceso constructivo, ya que podemos definir funciones auxiliares (de dos o más variables), como por ejemplo f(a, b, n) = (a+3b)/b^n.
Investigación:
- Sea la familia de curvas elípticas y² = x³ - p x - q (con p y q deslizadores). Comprobar que si A, B y C son los puntos de corte de una recta cualquiera con una de esas curvas, entonces la suma A+B+C permanece constante (mientras esté definida) para cualquier otra curva de la familia, es decir, para cualquier par de valores p y q.
