Suma

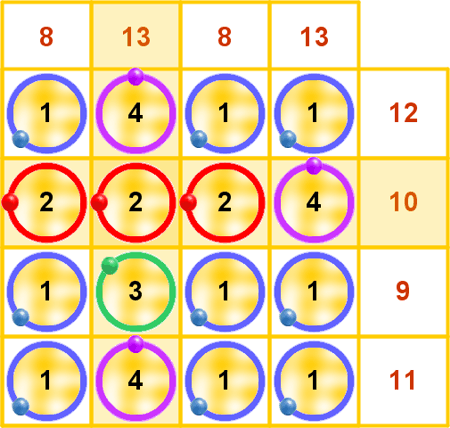
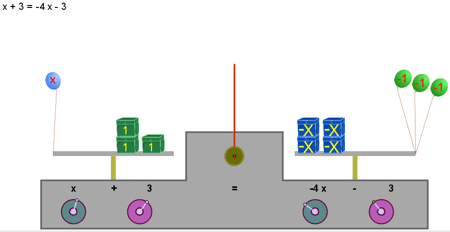
En este ejemplo, la construcción plantea al azar un ejercicio aritmético y comprueba el resultado. Mientras se realiza la comprobación el usuario no puede "ensayar" otros resultados.

Clic en la imagen para abrir el applet de GeoGebra

 Eje

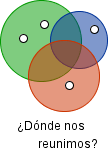
Las respuestas a las preguntas autoevaluables pueden no estar determinadas. En este ejemplo, la construcción valora positivamente cualquier diseño simétrico con respecto a un eje.

Clic en la imagen para abrir el applet de GeoGebra

 Sus + y sus -

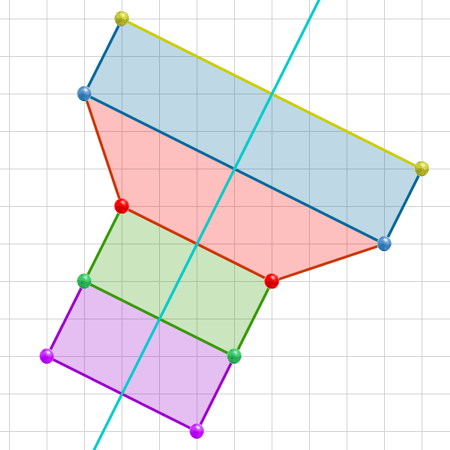
Podemos asociar un comportamiento determinado según sea la información sobre la posición de determinados objetos, lo que permite evaluar los resultados.

Clic en la imagen para abrir el applet de GeoGebra

 4x4

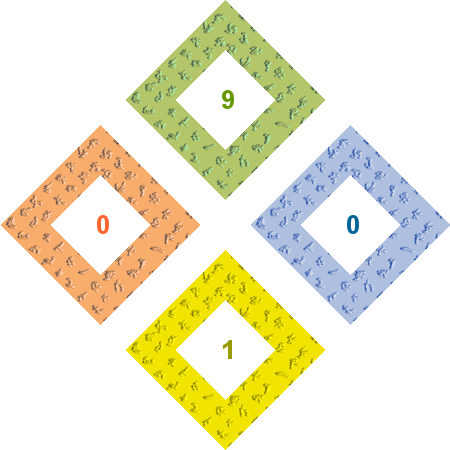
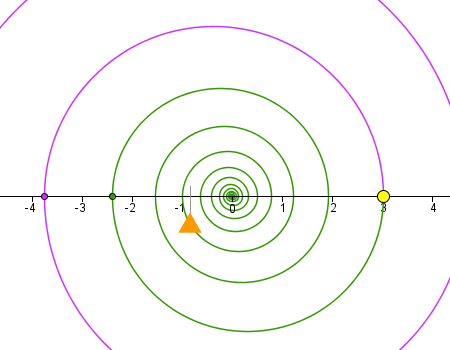
En este ejemplo la condición de visibilidad de cada número depende de la posición de un punto en un arco de la circunferencia que lo rodea. A cada posición le corresponde un valor determinado, por lo que la construcción puede evaluar si cada línea verifica o no la condición establecida.

Clic en la imagen para abrir el applet de GeoGebra

 Más, menos, por, entre

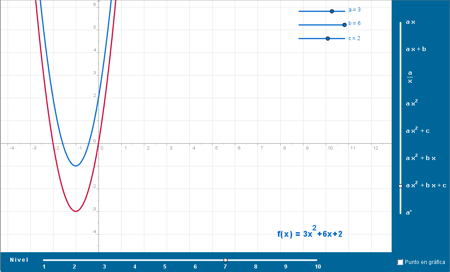
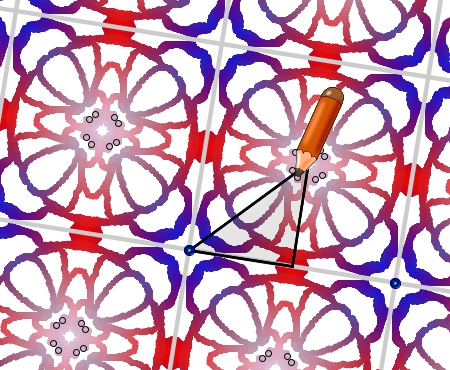
La visualización de modelos que representen relaciones abstractas ayuda a captar y profundizar en su significado.

Clic en la imagen para abrir el applet de GeoGebra

 Arco iris

Los fenómenos físicos suele estar "repletos" de Matemáticas. Desde Arquímedes a Einstein, los principios que rigen el universo han necesitado el lenguaje matemático para desentrañar su naturaleza. En este ejemplo se recrea un experimento realizado por el filósofo y matemático René Descartes .

Clic en la imagen para abrir el applet de GeoGebra

 Las dimensiones del hipercubo

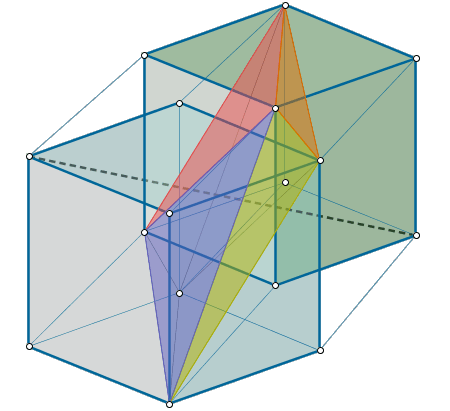
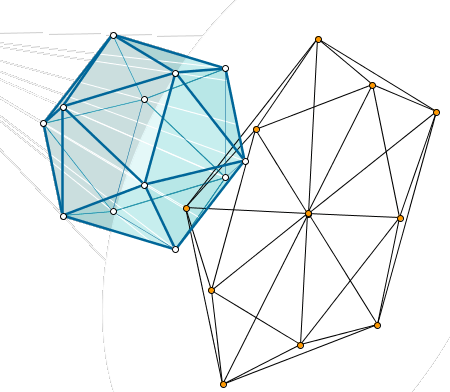
En este ejemplo se visualizan las secciones poliédricas de un hipercubo (dimensión 4). Para facilitar la observación del procedimiento empleado, podemos ver previamente ese mismo procedimiento aplicado a un segmento (dimensión 1), a un cuadrado (dimensión 2) y a un cubo (dimensión 3). Un aluvión de preguntas dirige la exploración.

Clic en la imagen para abrir el applet de GeoGebra

 La balanza

La manipulación de los elementos presentes en el escenario, junto con la inmediata respuesta (retroalimentación) visual a nuestras propias acciones, facilita la adquisición de representaciones mentales más significativas, no algorítmicas.

Clic en la imagen para abrir el applet de GeoGebra

 Sol y Luna

Esta es una de las tres actividades en las que se reproduce el método que usó el matemático griego Aristarco (siglo III a.C. ), tal vez el primero en proclamar que la Tierra orbita alrededor del Sol, para calcular el tamaño de la Luna y el Sol, así como la distancia que nos separa de ambos.

Clic en la imagen para abrir el applet de GeoGebra

 El juego de las funciones

En ocasiones, es el propio escenario el que plantea las preguntas...

Clic en la imagen para abrir el applet de GeoGebra

 Creador de mosaicos

Bellas Artes: arquitectura, escultura, pintura, literatura, música y danza, teatro, cine, matemáticas...

Clic en la imagen para abrir el applet de GeoGebra

 Ombra mai fu

Algunas construcciones son especialmente ricas en conexiones matemáticas. Esta es una de ellas.

Clic en la imagen para abrir el applet de GeoGebra

 Cerezas

Una simple colección de objetos puede convertirse en un estupendo juego de estrategia pura, con un montón de variantes posibles que podemos ajustar al nivel de los alumnos.

Clic en la imagen para abrir el applet de GeoGebra

 Dos siglos

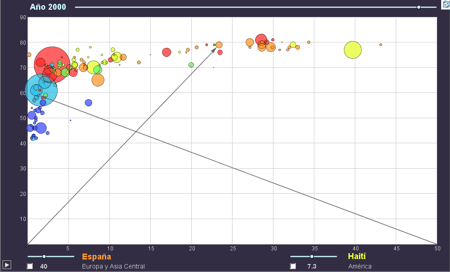
Los gráficos estadísticos reviven gracias al dinamismo que permite GeoGebra.

Clic en la imagen para abrir el applet de GeoGebra