|
FACILIDADE: Geometria CAS
Distâncias
Equidistâncias
Distâncias constantes
Eqs. algébricas e inequações
Ângulos
Distância do táxi
Corpos
VERSATILIDADE
Listas de poligonais
FLEXIBILIDADE: Geometria Elástica
Geometria elástica
Newton's Principia
Tensegridades |
Resumo
Desde o seu início, o GeoGebra
foi projetado especificamente para mostrar a representação dual, gráfica e
algébrica, dos objetos matemáticos. Nesta apresentação, com foco central,
vou destacar alguns procedimentos que exploram as possibilidades didáticas
dessa dualidade.
Esses procedimentos, apresentados a estudantes de 15 ou 16 anos, são tão
simples, atraentes e rápidos de criar que permitem que os próprios alunos os
gerem e utilizem do zero... com grande sucesso!
Apesar de sua simplicidade, veremos que são tão poderosos que nos permitem
mergulhar em profundidades matemáticas praticamente inabordáveis na sala de aula
do ensino médio sem a ajuda do GeoGebra, desde estruturas algébricas
(como corpos) até métricas não euclidianas (como a distância do
táxi). |
Nota: Todas as construções GeoGebra
vinculadas a esta página web foram criadas pela pessoa que as apresenta
aqui. Nenhuma delas, exceto a construção Bolhas, faz
uso de programação JavaScript.
O autor
Em meus 40 anos de ensino como Professor de Ensino Médio, na busca por
incentivar o interesse dos alunos, pesquisei a relação das Matemáticas com
outras áreas tão diversas quanto Jogos
 ,
Percepção ,
Percepção
 e Música
e Música
 .
A chegada da Geometria Dinâmica trouxe novas e grandes oportunidades para
atrair os estudantes e promover a criação de suas próprias construções. .
A chegada da Geometria Dinâmica trouxe novas e grandes oportunidades para
atrair os estudantes e promover a criação de suas próprias construções.
Minha relação com o GeoGebra remonta a 2005, quando conheci este programa
criado por Markus Hohenwarter [7], embora
já tivesse trabalhado com outros programas de geometria dinâmica. Dois
anos depois, em 2007, o professor Tomás Recio
 me convocou para o Centro Internacional de Encontros Matemáticos (CIEM
me convocou para o Centro Internacional de Encontros Matemáticos (CIEM
 ,
Cantábria) que reuniu, entre outros, vários professores de ensino médio
espanhóis pioneiros no uso educacional da geometria dinâmica. Nessa
reunião, defendi a eficácia do GeoGebra [10] em
comparação com outros programas como o Cabri. Uma consequência desse
encontro foi a formação do grupo G⁴D ,
Cantábria) que reuniu, entre outros, vários professores de ensino médio
espanhóis pioneiros no uso educacional da geometria dinâmica. Nessa
reunião, defendi a eficácia do GeoGebra [10] em
comparação com outros programas como o Cabri. Uma consequência desse
encontro foi a formação do grupo G⁴D  ,
composto por J.M. Arranz ,
composto por J.M. Arranz  , J.A. Mora , J.A. Mora  , M. Sada , M. Sada  e eu
e eu
 . .
Dois anos depois, a partir do Ministério da Educação da Espanha, Antonio Pérez  ,
na época diretor do Instituto de Tecnologias Educacionais (ITE, hoje INTEF ,
na época diretor do Instituto de Tecnologias Educacionais (ITE, hoje INTEF  ),
me encarregou de realizar cursos de formação em GeoGebra para professores
do Ensino Fundamental e Médio [11,
13], bem como
a criação de um conjunto de atividades completas (introdução ao tópico,
construção a ser explorada e questionário) para os alunos, classificadas
por temas e níveis, que denominamos Projeto Gauss [14,
1]. Simultaneamente, Tomás Recio lançou o primeiro
Instituto GeoGebra em língua espanhola, o Instituto GeoGebra de
Cantábria ),
me encarregou de realizar cursos de formação em GeoGebra para professores
do Ensino Fundamental e Médio [11,
13], bem como
a criação de um conjunto de atividades completas (introdução ao tópico,
construção a ser explorada e questionário) para os alunos, classificadas
por temas e níveis, que denominamos Projeto Gauss [14,
1]. Simultaneamente, Tomás Recio lançou o primeiro
Instituto GeoGebra em língua espanhola, o Instituto GeoGebra de
Cantábria  ,
do qual sou instrutor desde sua fundação. ,
do qual sou instrutor desde sua fundação.
Introdução
O principal objetivo desta conferência é mostrar a estreita relação entre
procedimentos algébricos e geométricos usando o GeoGebra. Grande parte do tempo
será dedicada à apresentação de atividades que podem ser abordadas por
estudantes do ensino secundário por meio de construções feitas por eles mesmos.
Além de poderem ser usadas esporadicamente para explorar conteúdos específicos,
esse tipo de construção ganha todo o seu poder educacional em um ensino de
matemática baseado na aquisição de competências.
Na primeira parte desta apresentação, detalharei procedimentos muito
simples que exploram a forte interconexão entre geometria e álgebra
que dá nome ao GeoGebra (daí o título de Principia) e
permitem que estudantes do ensino secundário (por volta dos 15 ou 16 anos)
realizem explorações matemáticas que, "em princípio", estão além de seu
alcance, deixando as poderosas ferramentas do GeoGebra realizarem os
cálculos álgebro-geométricos complexos, da mesma forma que atualmente
deixamos calculadoras e folhas de cálculo realizar cálculos aritméticos
complexos e tediosos.
Especificamente, a facilidade com que podemos criar retas e
circunferências paralelas nos ajudará a construir um offset
dinâmico cujo traço colorido permite visualizar uma variedade de lugares
geométricos. Ao mesmo tempo, o CAS (Sistema de Álgebra
Computacional), aplicado a distâncias euclidianas, nos auxiliará na
criação de curvas implícitas que se ajustam a esses lugares. Também
veremos como, em algumas ocasiões, essas curvas implícitas podem ser
convertidas em equações e inequações.
Ampliaremos o uso do CAS para lidar com ângulos e também abordaremos
outras distâncias não euclidianas, como a distância do táxi.
Encerraremos esta primeira parte com um exemplo recíproco, no qual
recorrer à geometria nos ajudará a visualizar e manipular os conceitos e
propriedades inerentes à estrutura algébrica de um corpo.
Na segunda parte, apresentarei algumas ideias para realizar construções um
pouco mais sofisticadas, mas não menos atrativas, que podem servir como
modelos a serem analisados ou modificados pelos alunos.
Primeiro, veremos como as listas no GeoGebra facilitam a
incorporação de uma grande quantidade de dados. Como exemplo,
representaremos a linha costeira dos continentes em uma única lista,
criando um modelo da Terra.
Em seguida, usaremos vetores para modificar instantaneamente a
posição dos pontos de acordo com nossos interesses, graças aos scripts
do GeoGebra. Esses vetores podem ser usados para combinar forças
repulsivas (como partículas com a mesma carga), forças atrativas (como as
usadas por Newton para formular sua lei da gravitação universal) ou
simplesmente forças reativas (como em colisões elásticas).
Além disso, podemos usar vetores para criar uma "geometria elástica".
Nessa abordagem, os pontos não têm uma posição definida, mas sua posição
em cada momento é o resultado da aplicação das forças mencionadas. Por
exemplo, na geometria elástica, um ponto não "está" em uma circunferência,
mas é irresistivelmente atraído por ela, tendo "seu limite" nela.
Por fim, como aplicação desse tipo de geometria elástica, veremos exemplos
de construção de tensegridades.
FACILIDADE: Geometria CAS
GeoGebra: Geometria e Álgebra
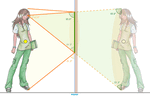
Desde o seu nascimento, o GeoGebra permite a construção rápida e simples
de modelos geométricos, o que facilita tanto a aprendizagem quanto o
ensino e a pesquisa. Essa facilidade promove o efeito IKEA
 (valorizamos mais o que somos capazes de construir por nós mesmos, daí o
sucesso dos jogos clássicos de construção, como o Meccano ou
o Lego).
Aqui é mostrada uma das construções que apresentei na reunião de 2007 no
CIEM [9] e que usei para defender o uso deste
programa no ensino. Escolhi esta construção porque Markus a popularizou,
mantendo-a por anos como parte do cabeçalho do site oficial do GeoGebra
(valorizamos mais o que somos capazes de construir por nós mesmos, daí o
sucesso dos jogos clássicos de construção, como o Meccano ou
o Lego).
Aqui é mostrada uma das construções que apresentei na reunião de 2007 no
CIEM [9] e que usei para defender o uso deste
programa no ensino. Escolhi esta construção porque Markus a popularizou,
mantendo-a por anos como parte do cabeçalho do site oficial do GeoGebra
 . .
Desde então, o GeoGebra se desenvolveu enormemente. Podemos construir uma
infinidade de modelos e aplicativos relacionados a áreas como Aritmética,
Equações, Funções, Isometrias, Variável Complexa, Estatística,
Probabilidade...
A variedade de procedimentos também é enorme: desde cortar um hipercubo em
fatias [15] até demonstrar automaticamente uma
proposição [12,
17, 18, 28].
É evidente que o que caracteriza a geometria dinâmica é
precisamente o seu dinamismo. Assim como na maioria dos animais que
possuem um sistema visual, a evolução levou a que um alerta mental seja
acionado quando qualquer objeto ou ser em nosso ambiente entra em
movimento. Portanto, o movimento é um meio natural e excelente para focar
a atenção.
No entanto, como podemos visualizar facilmente lugares geométricos
sem recorrer a construções complexas ou usar equações algébricas
complicadas? Veremos que uma possível resposta é usar o CAS.
Distâncias
O conceito matemático sobre o qual vou me concentrar é um conceito fundamental:
a distância.
|
Ao colocar um
ponto em um espaço, o conceito de distância a ele se comporta como o que
os físicos chamam de "campo": não se manifesta até que introduzamos
outro objeto nele.
Usaremos dois procedimentos simples para visualizar lugares geométricos
relacionados com a distância: a criação de curvas implícitas e o
uso do
offset dinâmico com traço ativado. |
Método clássico: sequências de curvas paralelas
(offset estático)
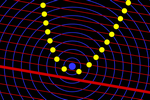
Utilizando o comando VetorUnitárioPerpendicular (e seu vetor oposto),
é simples criar sequências de retas paralelas a uma reta, a distâncias
progressivas. Para cada reta r,
encontramos um par de sequências:
Sequência(Translação(r, k
VetorUnitárioPerpendicular(r)),
k, 0, 20, 0.2)
Sequência(Translação(r, –k
VetorUnitárioPerpendicular(r)),
k, 0, 20, 0.2)
Graças ao comando VetorCurvatura e à ferramenta Lugar Geométrico,
podemos generalizar o paralelismo para muitas curvas (offset  ).
Se P é um ponto na curva c, as duas curvas paralelas a uma
distância k serão dadas pelo lugar geométrico dos pontos: ).
Se P é um ponto na curva c, as duas curvas paralelas a uma
distância k serão dadas pelo lugar geométrico dos pontos:
P ± k VetorUnitário(VetorCurvatura(P, c))
Note que, em geral, as curvas offset não são congruentes com a curva
original. Ou seja, as curvas paralelas não são simples translações, a
menos que sejam retas.
Mas, no caso da circunferência (com centro em O e raio 4),
cujo offset também é uma circunferência, não precisamos do comando
VetorCurvatura ou da ferramenta Lugar Geométrico, pois basta
variar adequadamente o raio da circunferência original:
Sequência(Circunferência(O, 4 + k), k, 0, 20,
0.2)
Sequência(Circunferência(O, 4 – k), k, 0, 20,
0.2)
Além disso, se considerarmos um ponto O como uma circunferência de
raio 0, obtemos uma única sequência de offsets centrados nele:
Sequência(Circunferência(O, k), k, 0, 20,
0.2)
|
Resumindo: podemos facilmente criar sequências de curvas paralelas a
retas, circunferências e pontos. |
Offset dinâmico com traço ativado
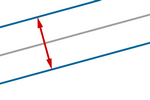
Agora, substituiremos cada sequência de curvas paralelas por uma única
curva paralela dinâmica. Como antes, usando o comando
VetorUnitárioPerpendicular (e seu vetor oposto), é simples criar
curvas paralelas a uma reta, a uma distância d dada.
Para cada reta r, encontramos um par de curvas paralelas:
Translação(r, d
VetorUnitárioPerpendicular(r))
Translação(r, –d VetorUnitárioPerpendicular(r))
Graças ao comando VetorCurvatura e à ferramenta Lugar Geométrico,
podemos generalizar o paralelismo para muitas curvas (offset). Se
P é um ponto na curva c, as duas curvas paralelas a uma
distância d serão determinadas pelo lugar geométrico dos pontos:
P ± d VetorUnitário(VetorCurvatura(P, c))
Observemos que, em geral, as curvas offset não são congruentes com a curva
original. Ou seja, as curvas paralelas não são simples translações, a
menos que sejam retas.
Mas, no caso da circunferência (com centro em O e raio 4),
cujo offset também é uma circunferência, não precisamos do comando
VetorCurvatura ou da ferramenta Lugar Geométrico, pois basta
variar adequadamente o raio da circunferência original:
Circunferência(O, 4 + d)
Circunferência(O, 4 – d)
Além disso, se considerarmos um ponto O como uma circunferência de
raio 0, obtemos um único offset centrado nele:
Circunferência(O, d)
|
Resumindo: podemos facilmente criar offsets de retas, circunferências e
pontos. |
Também podemos criar os pontos de interseção entre dois
objetos e o Lugar Geométrico (Locus) correspondente. O problema com
o uso do comando ou da ferramenta Lugar Geométrico é que, em muitas
situações mais complicadas do que a mostrada aqui, não é possível utilizá-los
adequadamente.
Como o GeoGebra é um programa de Geometria Dinâmica, não
apenas podemos mover objetos geométricos à vontade, mas também podemos
estabelecer animações automáticas [22].
Para fazer isso, ativamos o traço do offset e escolhemos
um valor d decrescente (oposto a um seletor "incrementar
uma vez"). Nota: alternativamente, podemos escolher um valor de
d crescente (incrementar uma vez) e atribuir a ele uma velocidade
de -1 em vez de 1.
Dessa forma, ao fazer offset simultaneamente em um ponto e uma reta, por
exemplo, podemos visualizar a parábola por contraste de cor.
|
A vantagem do
offset em relação à curva implícita, que veremos a seguir, é que nos
permite interromper a reprodução do procedimento a qualquer momento e
observar como os traços das linhas se cruzam para entender por que
esses pontos de interseção fazem parte do lugar geométrico procurado. |
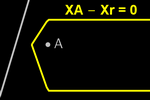
Curvas implícitas
a partir de definições em CAS

Uma parábola pode ser definida como o lugar geométrico dos pontos no plano
que estão equidistantes de uma reta (diretriz) e um ponto externo a ela
(foco). Localizar um ponto (o vértice) é fácil, mas como localizar os
outros?
Com o GeoGebra, podemos criar um ponto livre para explorar o terreno e
marcar as posições onde as distâncias são iguais. Isso é muito didático,
mas depois de vários exercícios pode se tornar tedioso.
Alternativamente, podemos construir um ponto genérico que crie o lugar
geométrico, mas essa construção só servirá para este caso ou casos
semelhantes.
Também podemos criar a curva implícita definindo, na
folha CAS,
um ponto arbitrário X(x,y):
X:= (x, y)
a distância de X ao foco F:
XF(x,y):= Distância(X, F)
a distância de X à diretriz r:
Xr(x,y):= Distância(X, r)
e igualando ambas distâncias:
XF – Xr = 0
O GeoGebra utiliza algoritmos numéricos para criar essa curva implícita,
portanto, em alguns casos, podem ocorrer pequenos erros ou omissões.
Nota: Pelo menos por enquanto,
o GeoGebra não representa equações desse tipo em três variáveis. Ou seja,
ele reconhece x² + y² + z² = 16 como uma
esfera, mas não reconhece como tal a equação equivalente
(sqrt(x² + y² + z²))² = 16.
Equidistâncias
Agora só precisamos usar essas ferramentas simples para investigar uma
variedade de situações com sua ajuda.
Daqui para frente, consideramos definidas as distâncias de um ponto
arbitrário X(x,y) a A e B como:
XA(x,y):= Distância(X, A)
XB(x,y):= Distância(X, B)
a uma reta r como:
Xr(x,y):= Distância(X, r)
e a uma circunferência c como:
Xc(x,y):= Distância(X, c)
Equidistância a dois ou três pontos

Ao contrair as circunferências com o traço ativado, em cada ponto do
plano permanece a cor correspondente ao centro mais próximo, assim obtemos
a mediatriz.
A curva implícita da mediatriz de AB tem a seguinte equação:
XA – XB = 0
No caso de três pontos, podemos visualizar o circuncentro [2]
do triângulo que eles determinam.
|
Já vimos... |
Equidistância a um ponto e uma reta

Ao aproximar simultaneamente uma reta paralela à
reta r e uma circunferência centrada em A, com o traço
ativado, a cor do objeto mais próximo (reta ou ponto) permanece,
resultando na correspondente parábola. Como já vimos, neste caso também é
simples construir esse locus.
|
Equidistância a um ponto e uma circunferência
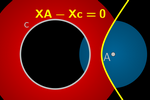
Se o ponto estiver dentro do círculo, obtemos uma elipse, e se estiver
fora, obtemos um braço de hipérbole.
A curva implícita da elipse ou do braço de hipérbole tem a seguinte
equação:
XA – Xc = 0
Note que uma construção semelhante à da parábola também nos permite gerar
esse lugar geométrico.
|
Mais... |
Equidistância a um ponto e a uma cônica
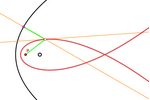
Essas construções dos lugares geométricos dos pontos que equidistam de
um ponto e de uma cônica são muito semelhantes à construção dos lugares
que equidistam de um ponto e de uma circunferência. No entanto, a
equação é muito mais complicada de encontrar.
|
Equidistância entre duas retas

Ao aproximar simultaneamente retas paralelas, com o
traço
ativado, a cor correspondente à reta mais próxima é preservada, resultando
nas bissetrizes. No caso de três retas, podemos visualizar o incentro e os
exincentros do triângulo que elas formam.
Como caso particular, podemos visualizar o eixo medial
 de um polígono como uma fronteira (composta por segmentos e arcos de
parábolas) entre os traços sobreviventes.
de um polígono como uma fronteira (composta por segmentos e arcos de
parábolas) entre os traços sobreviventes.
Da mesma forma que mencionado anteriormente, também podemos visualizar e
construir facilmente o lugar geométrico correspondente à bissetriz.
Equidistância entre reta e circunferência e entre
duas circunferências
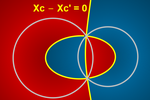
O lugar geométrico dos pontos que equidistam de uma reta e de uma
circunferência é geralmente formado por uma parábola, ou, se elas se
interceptam, por duas parábolas.
O lugar geométrico dos pontos que equidistam de duas circunferências é
geralmente formado por um braço de hipérbole ou, se elas se interceptam, por
uma elipse.
Diagrama de Voronoi
e mapas similares

Embora a curva implícita seja mais rápida de criar e usar, o método de
offset permite lidar com problemas que a curva implícita não pode abordar.
Por exemplo, se em vez da equidistância entre dois pontos (mediatriz),
aplicarmos o método de offset a vários pontos, obtemos o diagrama de Voronoi
(ou
polígonos de Thiessen).
Da mesma forma, também podemos criar o mapa das regiões mais próximas a
uma coleção de retas ou circunferências.
Nota: O comando Voronoi no GeoGebra não colore cada
região. É possível ver uma maneira dinâmica de fazê-lo aqui
 . .
Equidistância entre duas curvas

Podemos aplicar o método de offset a duas curvas, desde que possamos
calcular o vetor normal em cada ponto de ambas.
No caso em que não possamos calcular os vetores normais, sempre podemos
criar um mapa de calor usando a técnica do scanner de cores dinâmicas [3,
19, 26, 27,
31].
Distâncias constantes
Ponto-Ponto
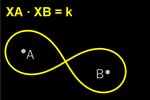
Quando a soma das distâncias dos pontos do lugar desejado aos
pontos A e B é constante, obtemos uma elipse.
Quando a diferença das distâncias dos pontos do lugar desejado aos
pontos A e B é constante, obtemos um braço de hipérbole. (No
caso em que a constante seja 0, obtemos a mediatriz.)
Quando o produto das distâncias dos pontos do lugar desejado aos
pontos A e B é constante, obtemos um oval de Cassini
 .
Se a constante coincidir com o quadrado da metade da distância AB, obtemos
uma lemniscata de Bernoulli .
Se a constante coincidir com o quadrado da metade da distância AB, obtemos
uma lemniscata de Bernoulli
 . .
Quando o quociente das distâncias dos pontos do lugar desejado aos
pontos A e B é constante, obtemos, surpreendentemente
 ,
uma circunferência. (No caso em que a constante seja 1, obtemos a
mediatriz.) ,
uma circunferência. (No caso em que a constante seja 1, obtemos a
mediatriz.)
Quociente constante ponto-reta

Quando a razão das distâncias dos pontos do lugar procurado ao ponto A
e à reta r é uma constante k, obtemos uma cônica, que será
uma elipse, uma parábola ou uma hipérbole, dependendo do valor de k
(excentricidade) ser menor, igual ou maior que 1, respectivamente
 . .
Combinação linear constante
Podemos generalizar as somas e diferenças para qualquer combinação linear
de distâncias entre pontos, ponto e reta, ponto e circunferência, etc.
Dessa forma, surgem cônicas e quárticas (ovais cartesianos, produtos de
retas...), o caracol de Pascal
 ,
bem como curvas de grau superior resultantes das anteriores. ,
bem como curvas de grau superior resultantes das anteriores.
|
Mais... |
Combinação linear logarítmica constante
 Também
podemos generalizar os produtos e quocientes para qualquer combinação
linear de logaritmos de distâncias. Também
podemos generalizar os produtos e quocientes para qualquer combinação
linear de logaritmos de distâncias.
|
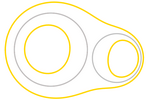
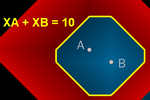
Soma constante de três ou quatro pontos
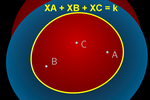
No caso da soma constante k das distâncias aos três pontos A,
B e C, basta introduzir:
XA + XB + XC = k
Para realizar o offset, o que
fazemos é sobrepor o traço das elipses Elipse(A, B, (k–h)/2) com as
circunferências Circunferência(C, h), onde h é um parâmetro real
positivo que diminui do valor k até zero. Os pontos de fronteira coloridos
serão então exatamente os pontos que satisfaçam:
Elipse(A, B, (k–h)/2) = Circunferência(C, h)
Isso é equivalente a que a soma
das distâncias desses pontos a A, B e C seja exatamente
a quantidade pré-determinada k (pois XA + XB = k – h, XC = h). Dessa
forma, conseguimos mostrar uma 3-elipse
 .
No caso de quatro pontos, os traços de duas elipses se sobrepõem,
determinando uma 4-elipse. .
No caso de quatro pontos, os traços de duas elipses se sobrepõem,
determinando uma 4-elipse.
Nota: Uma
abordagem algébrica dessa situação, também com o GeoGebra, pode ser vista
neste artigo [8] de Zoltán Kovács.
Eqs. algébricas e inequações
Equidistância a um ponto e uma circunferência:
equação algébrica
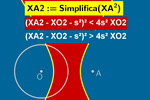
Anteriormente, definimos diretamente a distância de um ponto X(x,y)
à circunferência c como:
Xc(x,y):= Distância(X, c)
Com isso, a equação para os pontos equidistantes de um ponto e uma
circunferência se reduz a:
XA – Xc = 0
Se a circunferência tem centro O e raio s, podemos redefinir
a equação anterior como:
|XO – s| = XA
Essa redefinição nos permitirá visualizar as duas ramificações da
hipérbole. Para isso, basta transformar a equação irracional anterior em
uma equação algébrica, elevando ao quadrado para eliminar as raízes
(atingir a expressão a seguir é fácil, pois não requer processos de
agrupamento, simplificação ou cancelamento, mas também não há problema em
ajudar estudantes com poucos recursos em álgebra a resolver este pequeno
exercício, o resultado vale a pena):
(XA² – XO² – s²)² = 4s² XO²
As equações algébricas também têm a vantagem de permitir representar as
respectivas inequaçãos sem recorrer ao offset. Para isso, basta definir:
XA2(x,y) := Simplificar(XA^2)
XO2(x,y) := Simplificar(XO^2)
Dessa forma, podemos introduzir as inequaçãos:
(XA2 – XO2 – s²)² < 4s² XO2
(XA2– XO2 – s²)² > 4s² XO2
Restrições na
representação de desigualdades
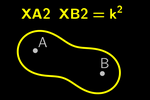
No entanto, nem sempre a equação algébrica permite que o GeoGebra
represente as inequaçãos correspondentes. Conforme aparece no manual
oficial
 ,
essa representação está limitada aos seguintes casos: ,
essa representação está limitada aos seguintes casos:
-
inequaçãos polinomiais em uma variável, como x³ > x + 1
-
inequaçãos quadráticas em duas variáveis, como x² + y² + x y < 4
-
inequaçãos ineares em uma das variáveis, como 2x > sen(y)
Ao encontrar a equação algébrica correspondente a XA – XB = k, obtemos a
mesma equação correspondente a XA + XB = k:
4 XB2 XA2 = (k² – XA2 – XB2)²
Esta equação se reduz a uma equação quadrática em duas variáveis, o que
permite ao GeoGebra representar suas inequaçãos correspondentes.
Nota: A equação quadrática comum à elipse e à
hipérbole não é nada mais do que a equação geral da cônica:
a x² + b x
y + c y² + d x + e y + f = 0
na
qual a elipse e a hipérbole se distinguem apenas pelo sinal do
discriminante b² – 4 a c.
No entanto, a equação algébrica correspondente a XA XB = k não representa
uma cônica, portanto, o GeoGebra não pode representar as inequaçãos
correspondentes. Por outro lado, a equação algébrica correspondente a XA =
k XB novamente é uma cônica, o que permite ao GeoGebra representar as
inequaçãos correspondentes.
Somas iguais de distâncias a dois pares de pontos

Se introduzirmos XA + XB = XC, o lugar geométrico resultante corresponde à
interseção de uma família de elipses XA + XB = k e uma família de
circunferências XC = k, à medida que o parâmetro k varia.
No caso de quatro pontos, XA + XB = XC + XD corresponderá à interseção de
duas famílias de elipses.
Nota: Os valores mínimo e máximo de k que garantem a
existência de interseção não são simples de calcular. Um enfoque
aproximado pode ser visto em [6].
Também é mostrado o caso XA + XB = XR, assim como a representação das
equações algébricas correspondentes.
Famílias de curvas

Em resumo, o campo a explorar pode ser expandido indefinidamente. Como
últimos exemplos envolvendo distâncias, aqui podemos observar alguns
resultados com potências.
É fácil demonstrar que a representação de XA2 + XB2 = k, com k constante,
é uma circunferência centrada no ponto médio de A e B.
Nota: O raio dessa circunferência é sqrt(k/2 − (x(A-B)/2)²
− (y(A-B)/2)²).
Disso, concluímos que o lugar onde a soma dos quadrados das distâncias a
vários pontos é constante é uma circunferência centrada no ponto médio
desses pontos.
Além disso, tomando D = XA2, podemos observar que a
representação no plano real de qualquer polinômio p(D) é composta
exclusivamente por uma ou mais circunferências.
Nota: Isso é uma consequência do teorema fundamental
do álgebra, uma vez que p(D) pode ser decomposto em fatores (D − c),
onde c é um número complexo. Se c for real e não negativo, então D − c = 0
corresponde a uma circunferência com raio igual à raiz quadrada de c; caso
contrário, nada é visualizado.
Aqui também vemos que podemos representar várias curvas de uma mesma
família, como, por exemplo, XAn = XB, e observar seu
comportamento simultaneamente.
Ângulos
A seguinte é uma das imagens geradas usando o scanner de cores dinâmico
que mais gosto. O scanner possui uma versatilidade incrível e é capaz de
criar um mapa de calor de praticamente qualquer situação.
[3,
19, 26, 27,
31].

Neste caso, o primeiro ponto isogónico I1 é visualizado através da
interseção dos lugares geométricos dos pontos a partir dos quais se vê sob
o mesmo ângulo cada par de
lados do triângulo.
Nota: I1 coincide com o ponto de Fermat
quando o maior ângulo do triângulo não excede 120º; caso contrário, o
ponto de Fermat coincide com o vértice correspondente a esse ângulo. Pode
ser calculado diretamente como o centro X(13)
 do triângulo:
do triângulo:
I1 = PontosNotáveisdoTriângulo(O, A, B, 13).

Entretanto, construir o scanner demanda algum trabalho. No entanto,
podemos usar o CAS para não apenas definir distâncias, mas também ângulos.
Se alguém ainda acha que usar a expressão XA em vez da expressão
sqrt((x − x(A))² + (y − y(A))²) também não economiza tanto trabalho,
talvez agora repense, já que pode usar a expressão OXA, definida na
folha CAS como:
OXA(x,y):= Ângulo(O, X, A)
em vez de sua equivalente algébrica (sendo O=(a, b) e A=(c, d)):
cos–1((a c – a x + b d – b y – c
x – d y + x² + y²) sqrt(a² c² – 2a² c x + a² d² – 2a² d y + a² x² + a² y²
– 2a c² x + 4a c x² – 2a d² x + 4a d x y – 2a x³ – 2a x y² + b² c² – 2b² c
x + b² d² – 2b² d y + b² x² + b² y² – 2b c² y + 4b c x y – 2b d² y + 4b d
y² – 2b x² y – 2b y³ + c² x² + c² y² – 2c x³ – 2c x y² + d² x² + d² y² –
2d x² y – 2d y³ + x⁴ + 2x² y² + y⁴) / (a² c² – 2a² c x + a² d²
– 2a² d y + a² x² + a² y² – 2a c² x + 4a c x² – 2a d² x + 4a d x y – 2a x³
– 2a x y² +
b² c² – 2b² c x + b² d² – 2b² d y + b² x² + b² y² – 2b c² y + 4b c x y –
2b d² y + 4b d y² – 2b x² y – 2b y³ + c² x² + c² y² – 2c x³ – 2c x y² + d²
x² + d² y² – 2d x² y – 2d y³ + x⁴ + 2x² y² + y⁴))
Naturalmente, essa expressão não passa de um desenvolvimento deduzido do produto
escalar de dois vetores:
vO(x,y):= Vetor(X, O)
vA(x,y):= Vetor(X, A)
OXA(x,y):= acos((vO vA)/(|vO|*|vA|))
A grande vantagem, além da conveniência, reside no fato de que o comando Ângulo
nos permite explorar as relações angulares sem precisar conhecer sequer as
operações básicas com vetores, como o produto escalar.
Aqui, por exemplo, podemos ver o lugar geométrico correspondente aos pontos que
formam com o segmento OA um ângulo igual (em radianos) à distância até o ponto
A:
OXA − XA = 0
Nota: As circunferências cujos arcos abrangem um ângulo
OXA equivalente a XA radianos têm centros em:
(O + A)/2 ± VetorPerpendicular(OA)/(2 tan(XA))
E aqueles que veem os segmentos OA e OB do mesmo ângulo:
OXA − OXB = 0
Finalmente, a interseção deste último lugar geométrico com o correspondente à equação OXA –
AXB = 0 é o ponto de Fermat procurado.
Distância do táxi
Nota: Esta seção surgiu devido ao confinamento decretado
em Espanha em 2020, em resposta à pandemia de covid-19. A Conselharia de
Educação das Astúrias, onde eu trabalhava como professor, decidiu substituir as
aulas presenciais por aulas remotas, ao mesmo tempo que decretou a proibição de
avançar com o currículo em qualquer disciplina. Isso me levou a buscar um campo
de exploração matemática fora do currículo oficial, mas acessível aos alunos do
4º ano do Ensino Secundário (com 15 ou 16 anos). Para os alunos, foi um
incentivo saber que estavam investigando um tópico praticamente desconhecido
para a grande maioria dos professores de matemática. Além disso, a mudança na
métrica trouxe muitas surpresas e perguntas. Uma festa matemática.
Agora, vamos sair da métrica euclidiana familiar:
|
A distância do
táxi (ou Manhattan) é especialmente simples de introduzir como projeto
de pesquisa no ensino secundário, uma vez que sua forma algébrica se
reduz a equações lineares. |
Distâncias de Minkowski
A forma da circunferência é determinante em qualquer geometria plana. Aqui
vemos a definição da distância de Minkowski
 de um ponto arbitrário
X(x,
y)
até a origem O. de um ponto arbitrário
X(x,
y)
até a origem O.
XO(x,y):= (|x|p+|y|p)1/p
Para p = 2, temos a distância euclidiana. Para p = 1, temos a distância do
táxi. Variando p, podemos observar como a forma da circunferência evolui
em cada caso.
Geometria do Táxi

Efetivamente, como Magritte diria, C'eci n'est pas un disque (isto
não é um disco)
 ,
mas veremos que pode ser a representação de um círculo se considerarmos a
métrica do Táxi. ,
mas veremos que pode ser a representação de um círculo se considerarmos a
métrica do Táxi.
Vou usar os prefixos T e E para distinguir a métrica
do Táxi da métrica Euclidiana.
Nota: Embora um T-círculo tenha uma forma quadrada,
Magritte ainda afirmaria, com razão, que o T-círculo que vemos é apenas
uma representação, uma imagem do disco; mas aqui, ao contrário de uma
pipa, o disco representado é uma abstração mental (uma forma matemática
ideal) em vez de algo material, o que torna a possível confusão ainda
maior.
Na métrica do Táxi (ou Manhattan
 )
as distâncias são medidas na horizontal e vertical, nunca na diagonal.
Assim, a T-distância de um ponto arbitrário (x, y) ao ponto O
é a soma das diferenças horizontais e verticais, em valor absoluto, de
suas coordenadas: )
as distâncias são medidas na horizontal e vertical, nunca na diagonal.
Assim, a T-distância de um ponto arbitrário (x, y) ao ponto O
é a soma das diferenças horizontais e verticais, em valor absoluto, de
suas coordenadas:
XO(x,y) := |x – x(O)| + |y –
y(O)|
|
Ao contrário
do que ocorre na métrica euclidiana, o GeoGebra não possui o comando
T-distância implementado, portanto, teremos que formular "manualmente"
tanto a distância entre dois pontos quanto a distância entre um ponto e
uma reta, fornecendo ambas as fórmulas aos alunos. |
Assim como o GeoGebra representa um segmento ajustando-o à grade de pixels
da tela, podemos imaginar um segmento na diagonal composto por segmentos
horizontais ou verticais tão pequenos quanto desejarmos: a T-distância
entre dois pontos B e C não mudará.
A T-distância entre B e C também será a mesma para qualquer arco crescente
ou decrescente de uma função cujo gráfico vá de B a C.
|
Na geometria
do táxi, pode haver infinitos caminhos mínimos entre dois pontos
diferentes. |
Tudo isso não simplifica a geometria, mas a complica. Isso ocorre porque o
comprimento de cada segmento não é uniforme na direção, mas depende de sua
inclinação.
Na E-ilusão mostrada [21], o quadrado azul parece
variar de tamanho, mas isso é apenas um problema de percepção que
desaparece quando vemos completamente seus lados (clique no quadrado
azul). Explicação: quando os cantos são visíveis, estimamos o tamanho do
quadrado pela diagonal; quando não são visíveis, o avaliamos pela
distância entre lados opostos (comprimento do lado).
No entanto, na geometria do táxi, o quadrado azul realmente varia sua área
dependendo da inclinação de seus lados (enquanto o T-comprimento de seus
lados e seus ângulos permanecem constantes).
Analisando o quadrado em detalhes, vemos que o T-perímetro do quadrado
azul e do quadrado amarelo é o mesmo, mas a área não é: a área do quadrado
amarelo é (b + c)², mas a área do quadrado azul é b² + c², que é mínima quando b = c. Portanto, na geometria taxista, as T-áreas coincidem com as
E-áreas, mas:
|
A área de um
T-quadrado NÃO é igual, em geral, ao quadrado do lado. |
Podemos imaginar a T-circunferência como uma compressão da
E-circunferência. Devido ao fato de que o T-comprimento não é uniforme em
cada direção, a T-circunferência é comprimida em uma forma quadrada, com
suas diagonais paralelas aos eixos cartesianos.
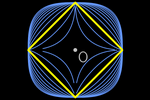
T-construções básicas
Se fixarmos um ponto O no plano, podemos considerar a distância do táxi do
restante dos pontos para O.
Como vimos, os pontos que estão T-equidistantes de O formam um quadrado
(com diagonais paralelas aos eixos). Se o raio for r, o perímetro é 8r,
então a razão entre a T-circunferência e o seu T-diâmetro é 4 (em vez de 𝜋).
Ao fixar outro ponto I diferente de O, estabelecemos uma orientação de O→I
e uma reta. Tomaremos a T-distância de O a I como unidade. Podemos
continuar pensando nas T-retas como se fossem E-retas, já que apenas o
modo de medir cada segmento muda. Lembre-se de que os pixels fazem com que
a própria reta desenhada pelo GeoGebra seja composta por segmentos
horizontais e verticais!
Dado um ponto A na reta r, existe apenas um outro ponto A' a mesma
distância de O que A. Este T-simétrico coincide com o E-simétrico.
Dado dois pontos distintos A e B, podemos encontrar todos os pontos que
estão equidistantes deles.
Essa T-mediatriz não coincide com a euclidiana.
Ao intersectar a T-mediatriz com a reta, obtemos o ponto médio, que
coincide com o ponto médio euclidiano.
As perpendiculares e paralelas são as mesmas da geometria euclidiana, mas
a projeção ortogonal de um ponto em uma reta não fornece, em geral, o
ponto mais próximo na reta. (Além disso, "o ponto mais próximo" também não
está unicamente determinado quando a reta tem declive 1 ou -1.)
Para realizar uma T-inversão
 ,
levamos A e I até a linha horizontal que passa por O, invertemos (x(A),
y(O)) na E-circunferência pontilhada, com centro em O que passa por (x(I),
y(O)), e criamos triângulos semelhantes que garantem a nova inversão. ,
levamos A e I até a linha horizontal que passa por O, invertemos (x(A),
y(O)) na E-circunferência pontilhada, com centro em O que passa por (x(I),
y(O)), e criamos triângulos semelhantes que garantem a nova inversão.
O T-inverso de A não coincide com o E-inverso de A.
T-ângulos

No T-círculo unitário, podemos definir o T-radiano da mesma forma que
definimos um E-radiano no E-círculo. Para T-medir um ângulo, basta medir o
T-comprimento do arco (reto) correspondente no T-círculo unitário. Um
T-círculo tem 8 T-radianos.
A perpendicularidade e a paralelismo são preservados sob rotações, mas, em
geral, as T-distâncias não
são invariantes em relação às E-rotações... nem em relação às T-rotações!
De fato, uma das peculiaridades da T-distância é que ela é sensível à
orientação das retas: um segmento, quando T-girado, já não mede o mesmo.

Quadrinho de Mafalda, por Quino
"Olha, eu penso nisso, e não há jeito!
Como diabos o tempo dobra as esquinas nos relógios quadrados?"
A soma dos ângulos de qualquer T-triângulo é de 4 T-radianos. Um
T-triângulo pode ser equilátero ou equiangular, mas nunca pode ser
regular.
Qualquer E-quadrado também é um T-quadrado. No entanto, como a distância
do táxi não é uniforme em qualquer direção, esses dois T-quadrados têm o
mesmo perímetro (embora não a mesma área):

O quadrado à esquerda é também um T-círculo.
O da direita não o é.
As T-funções trigonométricas são muito mais simples do que suas
equivalentes euclidianas. Por exemplo, a função T-seno não é apenas
transcendental, mas é linear por partes. A função T-tangente é formada,
por partes, por E-hipérboles euclidianas.
Nota: Uma possível expressão para a
função T-seno é: tsen(x) = 1 - 2 |1/2 - x/4 + 2 floor(1/4 + x/8)|. Assim,
a função T-cosseno pode ser definida como tcos(x) = tsen(x+2). A função
T-tangente é, por partes, uma função homográfica
 . .
T-equidistâncias
Ao encurtar as T-circunferências com o traço ativado, em cada ponto do
plano permanece a cor correspondente ao centro mais próximo.
Com vários pontos, podemos visualizar o diagrama de Voronoi e compará-lo
com o correspondente à distância euclidiana.
Para analisar a equidistância ponto-reta, precisamos conhecer a distância
de um ponto (x, y) a uma reta r: a x + b y + c = 0. Essa distância é (esta
fórmula é fornecida aos alunos e pode ser introduzida diretamente na
folha algébrica):
Xr(x,y) = |a x + b y + c| / Máximo(|a|, |b|)
Da equidistância ponto-reta surge a T-parábola, enquanto da equidistância
ponto-circunferência surgem a T-elipse e a T-hipérbole.
Se considerarmos a equidistância em relação aos lados de um polígono,
surge o seu esqueleto e o seu eixo medial. Podemos percorrê-lo com um disco
bitangente para verificá-lo.
Finalmente, também podemos encontrar o caminho T-equidistante entre duas
curvas, seja por meio de offset (como mostrado aqui) ou gerando um mapa de
calor.
T-cônicas
Como já vimos, a T-circunferência tem a forma quadrada (com as diagonais
paralelas aos eixos).
A T-elipse tem, em geral, a forma de um octógono. Se A e B estiverem na
mesma vertical ou horizontal, ela assume a forma de um hexágono. Quando a
soma constante coincide com a T-distância de A para B, a elipse degenera
em um retângulo com diagonal AB.
A T-parábola é formada, em geral, por duas semirretas (horizontais ou
verticais) e dois segmentos.
Por último, cada braço da T-hipérbole é formado, em geral, por duas
semirretas (horizontais ou verticais) e um segmento.
|
Mais... |
Combinação linear T-constante

Assim como fizemos na geometria euclidiana, podemos
generalizar a soma ou diferença constante para qualquer combinação linear.
Combinação linear logarítmica T-constante
Aqui é importante destacar que as distâncias
inversamente proporcionais a dois pontos NÃO resultam em
T-circunferências, como acontece com a métrica euclidiana.
Isso significa que a possível definição de
circunferência como o conjunto de pontos no plano cujo quociente das
distâncias a dois pontos fixos é constante não é válida para todas as
métricas.
|
T-esfera
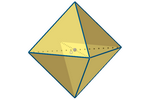
Uma T-esfera é formada pelos pontos do espaço que estão T-equidistantes do
seu centro. Ela tem a forma de um E-octaedro regular (que não é T-regular,
já que triângulos T-regulares não existem), com suas diagonais paralelas
aos eixos. Também pode ser gerada T-rotacionando uma T-circunferência ao
longo do diâmetro horizontal ou vertical.
|
Os lugares
geométricos que surgem na geometria do táxi nos convidam a perguntar: o
que "algo" precisa ter para ser esse "algo"? O que caracteriza um
objeto? Por exemplo, a E-esfera é considerada redonda porque seus pontos
estão equidistantes de seu centro, ou ela é redonda devido à
uniformidade na direção da distância euclidiana? |
T-elipsoide
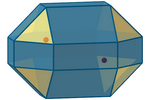
Um T-elipsoide é o lugar geométrico dos pontos no espaço cuja soma das
T-distâncias aos focos é constante (k). Em geral, ele tem a forma de um
poliedro com 18 faces retangulares e 8 faces triangulares (E-regulares,
mas não T-regulares).
O T-elipsoide degenera em um E-cuboctaedro quando as diferenças absolutas
das coordenadas dos focos coincidem; degenera em um E-cubo quando essas
diferenças também coincidem com k; e degenera em uma T-esfera (E-octaedro
regular) quando os focos coincidem.
Para certas posições especiais dos focos, um T-elipsoide com todas as suas
faces formadas por E-polígonos regulares aparece, mas ele não é um
E-poliedro regular nem semirregular, pois seus vértices não são uniformes.
Finalmente, quando a T-distância entre os focos é igual a k, obtemos um
ortoedro.
Corpos
Vamos voltar à nossa métrica euclidiana familiar. Até agora, usamos
álgebra para facilitar a observação de lugares geométricos. Vamos agora
ver um exemplo do processo recíproco: usar a geometria para facilitar a
observação de estruturas algébricas.
Normalmente, pensamos em estruturas algébricas (grupos, anéis, corpos...)
como algo inerente a certas estruturas numéricas, como números inteiros ou
números reais.
No entanto, podemos criar facilmente estruturas geométricas equivalentes,
com a vantagem de que assim podemos visualizar cada operação
aritmética como uma construção geométrica.
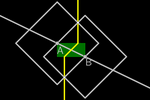
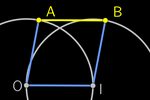
Construções preliminares
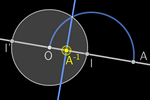
Se fixarmos um ponto O no plano, podemos considerar a distância
(euclidiana) do restante dos pontos até O. Denotaremos OP como a
distância de O até P.
Os pontos que equidistam de O formam uma CIRCUNFERÊNCIA.
Ao fixarmos outro ponto I diferente de O, estabelecemos uma DIREÇÃO, uma
ORIENTAÇÃO O→I e uma RETA r.
Tomaremos a distância OI como UNIDADE. Além disso, dois pontos na reta
limitam uma semicircunferência. Um ponto P está na reta r se
cumprir uma das seguintes igualdades:
OI = OP + PI (P está entre O e I)
OP = OI + IP (I está entre O e P)
PI = PO + OI (O está entre P e I)
-
Simétrico: Se A está na reta, nela existe apenas outro ponto A' à mesma
distância de O que A.
Mediatriz: Dados dois pontos distintos A e B, podemos encontrar todos os
pontos que equidistam deles.
Ponto médio: Intersectando a mediatriz com a reta r, obtemos o ponto médio MAB.
Perpendicular: A mediatriz nos permite traçar perpendiculares (basta
traçar a circunferência com centro P em um ponto qualquer de r).
Paralela: Com duas perpendiculares, obtemos uma reta paralela à r.
Inversão
 :
Com a circunferência e a perpendicular, podemos construir a inversão de A, A–1. :
Com a circunferência e a perpendicular, podemos construir a inversão de A, A–1.
O corpo dos pontos de uma reta
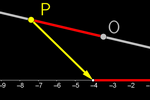
Continuaremos com nosso processo de construção da estrutura. Agora
definiremos as quatro operações elementares.
-
Soma: Para obter A + B, refletimos O em MAB para obter um
novo ponto em r.
-
Subtração: Para obter A − B, somamos A + B'.
-
Multiplicação: Criamos o produto construindo triângulos semelhantes,
obtendo um novo ponto em r.
-
Divisão: Para obter A/B, multiplicamos A x B–1. A divisão
não é comutativa.
-
Ordem: A simetria I' O I permite definir uma RELAÇÃO DE ORDEM:
A ≤ O :⇔AI' ≤ AI A ≤ B :⇔A − B ≤ O
Estrutura: Com base em tudo o que foi mencionado anteriormente, o conjunto
de pontos da reta r, dotado das operações de adição e multiplicação
definidas dessa maneira, constitui uma estrutura semelhante ("corpo
ordenado") à dos números reais ℝ. Na verdade,
podemos estabelecer uma bijeção (isomorfismo) entre essas duas estruturas:
(r, O, +, ×) → (ℝ, +, ×)
associando a cada ponto P de r o número real -OP se P<O e o número real OP
se P≥O.
Nota: Observamos que não abordamos a questão mais
complexa de como construir geometricamente todos os pontos da reta
(completude da reta real). Assumimos que a cada ponto corresponde um
número e vice-versa. No entanto, se desejarmos restringir-nos aos pontos
construíveis com as operações indicadas, podemos estabelecer um
isomorfismo desses pontos (que não seria toda a reta) com o corpo dos
números construíveis.
|
Os pontos de
uma reta não são os únicos objetos geométricos aos quais podemos
atribuir a estrutura de corpo. Podemos aplicar isso a qualquer conjunto
de objetos que compartilhem a mesma definição na qual existe apenas um
ponto livre residente em uma reta. Abaixo, alguns exemplos. |
|
Mais... |
O corpo das mediatrizes equidistantes de um ponto
fixo e outro livre em uma reta fixa
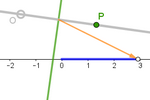
Seja r a reta que passa pelos pontos fixos O e I.
Seja A um ponto em r. Chamaremos mA à mediatriz do segmento OA.
Agora, basta aplicar todas as operações já vistas
entre dois pontos A e B às correspondentes entre as mediatrizes mA e mB.
Se coincidirmos a origem das coordenadas com O e o
ponto (1,0) com I, o ponto P corresponderá a (p,0), de modo que podemos
representar a mediatriz mP com a equação: x = p/2.
O corpo das parábolas equidistantes de uma reta
fixa e um ponto livre em uma reta perpendicular
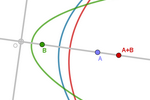
Seja r a reta que passa pelos pontos fixos O e I.
Seja a reta d, perpendicular a r no ponto O, e seja A um ponto em r.
Chamaremos dA à parábola com foco em A e diretriz d.
Agora, basta aplicar todas as operações já vistas
entre dois pontos A e B às correspondentes entre as parábolas dA e dB.
Se coincidirmos a origem das coordenadas com O e o
ponto (1,0) com I, o ponto P corresponderá a (p,0), de modo que podemos
representar a parábola dP com a equação: y² = 2p x − p².
O corpo das cônicas equidistantes de uma
circunferência fixa e um ponto livre em uma reta diametral
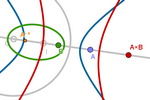
Seja a circunferência com raio s centrada em O, e
seja A um ponto na reta r que passa por O e I. Chamaremos sA à cônica com
semieixo s e focos em O (fixo) e A.
Agora, basta aplicar todas as operações já vistas
entre dois pontos A e B às correspondentes entre as cônicas sA e sB.
Se coincidirmos a origem das coordenadas com O e o
ponto (1,0) com I, o ponto P corresponderá a (p,0), de modo que podemos
representar a cônica sP com a equação correspondente: (2x-p)²/s² −
4y²/(p²-s²) = 1.
|
VERSATILIDADE
Listas de poligonais
As listas permitem agrupar uma grande quantidade de dados em um
único objeto. Neste exemplo, as poligonais simples, apesar de não
terem a elegância presente em muitas curvas, compensam com a versatilidade
proporcionada pela sua organização em uma única lista.
A poligonal fechada estática
Podemos importar grandes quantidades de dados para uma folha de cálculo.
Neste caso, 6122 coordenadas geográficas provenientes de dados públicos da
North American Cartographic Information Society
 que, uma vez depuradas em um processador de texto e devidamente
organizadas, são convertidas em listas.
que, uma vez depuradas em um processador de texto e devidamente
organizadas, são convertidas em listas.

Cada lista de pontos é chamada pelo comando LinhaPoligonal, de modo
que, finalmente, obtemos uma lista de poligonais cujos argumentos são listas
de pontos. Lembramos que, ao contrário do polígono, os vértices da linha
poligonal não precisam estar no mesmo plano. Assim, obtemos um único
design: o das costas terrestres. Graças a esse design, transformamos uma
esfera anódina em um modelo da superfície terrestre.
Costa = {LinhaPoligonal((5; 3.142; 1.204), (5; 3.117; 1.211), (5;
3.067; 1.22), (5; 3.031; 1.219), (5; 2.975; 1.223), (5; 2.967; 1.216), (5;
2.981; 1.204), (5; 2.96; 1.199), (5; 2.93; 1.214), (5; 2.896; 1.212), (5;
2.863; 1.216), (5; 2.832; 1.215), (5; 2.809; 1.212), (5; 2.787; 1.217), (5;
2.79; 1.23), (5; 2.775; 1.237), (5; 2.74; 1.24), (5; 2.67; 1.236), (5;
2.624; 1.25), (5; 2.609; 1.26), (5; 2.452; 1.271), (5; 2.429; 1.264), (5;
2.441; 1.248), (5; 2.413; 1.25), (5; 2.4; 1.245), (5; 2.366; 1.251), (5;
2.336; 1.246), (5; 2.308; 1.254), (5; 2.291; 1.236), (5; 2.264; 1.242), (5;
2.242; 1.256), (5; 2.252; 1.264), (5; 2.244; 1.275), ...
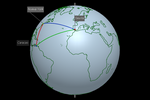
Com esse modelo [16], já podemos criar um cenário
onde podemos realizar uma variedade de atividades. Desde observar
elementos geográficos (polo, meridiano, paralelo, ponto cardeal, equador,
trópico, círculo polar, fuso horário...), até realizar análises e medições
(octante, latitude, longitude, rumo, loxodromia, distâncias ortodrômicas,
triângulo esférico...).
Nota: Este modelo pode servir como um excelente
exemplo do espírito de colaboração que caracteriza os recursos criados
pela comunidade GeoGebra desde o seu início. Usando-o como modelo, Chris
Cambré publicou, em neerlandês e inglês, um livro GeoGebra sobre projeções
cartográficas
 e outro sobre Mercator
e outro sobre Mercator
 .
Em seguida, Carmen Mathias traduziu ambos para o português ( .
Em seguida, Carmen Mathias traduziu ambos para o português ( , ,
 ).
Fechando o círculo, eu os traduzi para o espanhol ( ).
Fechando o círculo, eu os traduzi para o espanhol ( , ,
 ).
Esse comportamento colaborativo atinge sua expressão máxima no fórum do
GeoGebra. ).
Esse comportamento colaborativo atinge sua expressão máxima no fórum do
GeoGebra.
 . .
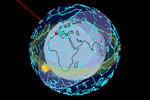 Se
adicionarmos agora a órbita solar aparente, teremos uma esfera armilar Se
adicionarmos agora a órbita solar aparente, teremos uma esfera armilar
 (ou astrolábio esférico) que nos permite analisar a passagem do tempo (anos,
dias, horas, GMT, UTC, estações do ano, zênite, obliquidade da eclíptica,
ponto Áries, equinócio, solstício, coordenada celestial, analema, horizonte
celeste, nascer do sol, pôr do sol, as 88 constelações, o
zodíaco, as estrelas mais brilhantes...) [20].
(ou astrolábio esférico) que nos permite analisar a passagem do tempo (anos,
dias, horas, GMT, UTC, estações do ano, zênite, obliquidade da eclíptica,
ponto Áries, equinócio, solstício, coordenada celestial, analema, horizonte
celeste, nascer do sol, pôr do sol, as 88 constelações, o
zodíaco, as estrelas mais brilhantes...) [20].
Nota: Os dados de Ascensão Reta e Declinação de
cada estrela foram coletados daqui.
A poligonal estática autogerada

Às vezes, podemos economizar o trabalho de importar os vértices. A
iteração de um script associado a um seletor animado
(desenvolveremos esse procedimento mais adiante) permite criar facilmente
construções em que a lista de vértices de uma poligonal seja ampliada
sucessivamente por si mesma. Um exemplo típico de aplicação desse método é
a geração de fractais, como este que mostra o procedimento iterativo para
criar o famoso floco de neve de Koch e o correspondente antifloco [29].
FLEXIBILIDADE: Geometria
Elástica
Geometria elástica
Normalmente, um ponto está ou não está em uma posição específica.
No entanto, graças aos scripts e vetores, podemos flexibilizar essa
situação, dando aos pontos a capacidade de se moverem livremente e, ao
mesmo tempo, tentando manter uma relação constante com outros pontos.
|
Em vez de
definir uma posição fixa para cada ponto, vamos estabelecer uma
relação com os demais pontos. |
Scripts e vetores
Nosso objetivo é criar um polígono equilátero com todos os seus
vértices livres. Como podemos fechar a poligonal mantendo seus vértices
livres (como um medidor de carpinteiro)?
Ou, começando com um polígono: como construir um losango mantendo o quarto
vértice livre?
A solução está em usar scripts. Por exemplo, um ponto livre Q permanecerá
sempre a 5 unidades do ponto livre P se atualizarmos a posição de P usando
o seguinte script:
DefinirValor(Q, P + 5 VetorUnitário(Q−P))
e ao atualizar a posição de Q, executamos o seguinte script:
DefinirValor(P, Q + 5 VetorUnitário(P−Q))
Dessa forma, em um losango, podemos manter a distância entre os vértices A
e B ao mesmo tempo em que ambos os pontos permanecem livres.
Ou podemos representar tipos de triângulos (retângulos, isósceles,
equiláteros...) que mantenham sua tipologia enquanto podemos mover
qualquer um de seus três vértices.
Este método também funciona para manter ângulos em vez de distâncias.
Basta modificar o vetor a ser aplicado ao ponto, usando a rotação adequada
para ajustar o ângulo. Como exemplo, podemos ver um pentágono equiangular
com todos os seus vértices livres.
Incluímos aqui um resultado (publicado em 2015) que é um belo exemplo da
estreita relação entre geometria e álgebra: "um polígono de n lados é
equiangular se e somente se e2𝜋i/n é uma raiz complexa
do polinômio de grau n-1, cujos coeficientes são os comprimentos dos lados
consecutivos do polígono"
 . .
Articulações
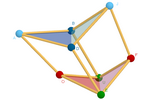
Um exemplo no espaço. Esta construção é baseada no princípio anterior para
preservar a distância (não os ângulos) entre os vértices de um cubo.
Isso resulta em um cubo articulado, cujas faces não são necessariamente
planas, mas dobradiças formadas por dois triângulos isósceles. As
possíveis posições de seus vértices são difíceis de analisar sem recorrer
a esse método
[4, 5, 32].
Scripts de seletores animados
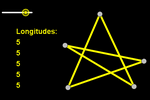
No entanto, não podemos generalizar esse método para polígonos com mais de
4 lados, pois o ajuste do comprimento do quinto lado pode desajustar os
lados já ajustados. Precisaríamos de um ajuste contínuo, iterativo,
até obter o resultado desejado. Podemos conseguir esse ajuste contínuo
usando um script que é executado continuamente, pois está associado à
atualização do valor de um seletor animado.
Por exemplo, na primeira cena, parece que P é um ponto na circunferência
(com raio 4 centrada em A),
mas na realidade é um ponto livre. Ao puxá-lo, ele voltará à
circunferência, pois o script do seletor animado é executado continuamente
e é o seguinte:
DefinirValor(P, P + u)
onde:
u = A - P + 4 VetorUnitário(P
− A)
Podemos adicionar um coeficiente (k) para controlar a velocidade:
DefinirValor(P, P
+ k u)
Se adicionarmos outro vetor, P se moverá em direção à interseção mais
próxima, mesmo que não haja uma interseção real!
Fazendo o mesmo com 5 pontos e 5 vetores, voilà! Agora podemos manter a
equidistância em mais de quatro pontos.
Fluido

Ao mascarar o polígono ou a poligonal com curvas, como usando splines
 ,
suavizamos a percepção do efeito da soma das forças internas (que mantêm a
distância entre os pontos) com as externas (que aplicam um movimento ao
conjunto). ,
suavizamos a percepção do efeito da soma das forças internas (que mantêm a
distância entre os pontos) com as externas (que aplicam um movimento ao
conjunto).
Amorfo
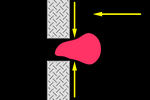
A versatilidade assim alcançada é grande. Por exemplo, podemos fazer com
que as figuras "passem pelo aro". Lembre-se de que em nenhum momento
determinamos a forma do conjunto, mas esta é resultado da soma vetorial
correspondente à posição alcançada a cada momento.
Polígono funicular
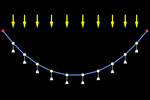
Neste exemplo, começamos com um fio sem massa apreciável do qual pendem
pesos (os vértices da poligonal). O script associado ao seletor animado faz com que esses vértices se movam verticalmente para
baixo, simulando a gravidade (força externa), ao mesmo tempo em que as
forças de coesão entre os vértices vizinhos (forças internas do fio)
limitam esse movimento.
Como podemos ver, após alguns segundos, a poligonal assume a forma do
polígono funicular
 resultante. Os vértices se ajustam muito bem a uma elipse. Se adicionarmos
mais vértices, o ajuste se aproximará cada vez mais da parábola teórica
(cargas pontuais infinitas distribuídas uniformemente na horizontal). A
catenária também não está longe (seria o resultado de remover o peso dos
vértices e adicionar peso uniforme ao fio poligonal: as cargas são
distribuídas uniformemente, mas não na horizontal, mas ao longo da curva,
ou seja, separadas pela mesma quantidade de arco em vez da mesma
quantidade horizontal).
resultante. Os vértices se ajustam muito bem a uma elipse. Se adicionarmos
mais vértices, o ajuste se aproximará cada vez mais da parábola teórica
(cargas pontuais infinitas distribuídas uniformemente na horizontal). A
catenária também não está longe (seria o resultado de remover o peso dos
vértices e adicionar peso uniforme ao fio poligonal: as cargas são
distribuídas uniformemente, mas não na horizontal, mas ao longo da curva,
ou seja, separadas pela mesma quantidade de arco em vez da mesma
quantidade horizontal).
Newton's Principia
Se existe uma área da matemática em que a álgebra e a geometria
tradicionais se fundem de forma natural, é na geometria analítica,
o núcleo dos programas de geometria dinâmica como o GeoGebra.
Um dos conceitos-chave da geometria analítica é o de vetor. Sua
representação gráfica, na forma de uma seta, convida a pensar em
movimento, em dinamismo. Usaremos vetores para criar procedimentos
dinâmicos, muito simples, mas ao mesmo tempo muito poderosos, para abordar
algumas situações.
Soma vetorial

Os ponteiros de um relógio analógico podem ser usados como um exemplo de
vetores. A ponta do ponteiro das horas percorre uma circunferência, assim
como a ponta do ponteiro dos minutos. Se somarmos ambos os vetores,
obtemos um lugar geométrico mais complexo (o locus se
intersecciona em 11 pontos, desde que o ponteiro dos minutos seja mais
longo que o ponteiro das horas, em 11 direções diferentes, o que significa
que em 12 horas a soma vetorial dos dois ponteiros coincide até 121
vezes). Se adicionarmos o ponteiro dos segundos, a soma vetorial percorre
um locus ainda mais complicado.
As somas vetoriais abrem a porta para a simulação de equilíbrios de
forças. Graças aos vetores, podemos simular forças, sejam elas atrativas
ou repulsivas, que fazem com que um ponto tenda a ocupar uma posição (ou
um trajeto) relativamente estável, ou seja, equilibrada em relação a
outras forças ou restrições.
Confinamento circular entre pontos que se repelem
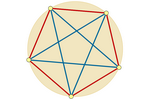
Podemos imaginar os pontos como partículas carregadas que se repelem entre
si e estão confinadas a um círculo. A cada ponto associamos a soma dos
vetores de repulsão com os outros pontos. Assim, os pontos se reorganizam
automaticamente em busca da posição de equilíbrio. Como era de se esperar,
essa posição sempre corresponde aos vértices de um polígono regular
inscrito na circunferência.
Confinamento quadrado entre pontos que se repelem
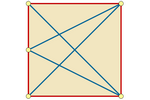
Se trocarmos o círculo por uma forma menos simétrica, como um quadrado,
distribuições regulares já não são possíveis em todos os casos. No
entanto, a posição de equilíbrio ainda é alcançada sempre na fronteira
periférica.
Confinamento esférico entre pontos que se repelem

Se passarmos do círculo para a esfera (problema de Thomson
 ,
um caso particular de um dos dezoito problemas matemáticos não resolvidos
propostos pelo matemático Steve Smale ,
um caso particular de um dos dezoito problemas matemáticos não resolvidos
propostos pelo matemático Steve Smale
 em 2000), a regularidade perfeita já não é possível, já que não existem
sólidos platônicos com 5 ou 7 vértices, por exemplo.
em 2000), a regularidade perfeita já não é possível, já que não existem
sólidos platônicos com 5 ou 7 vértices, por exemplo.
Mas, além disso, também não é verdade que o equilíbrio seja sempre
alcançado na perfeição regular! Na verdade, com 8 vértices, não é o cubo a
configuração que alcança o equilíbrio. Observemos também que na maioria
dos casos aparecem poliedros com faces triangulares (mas em geral não
equiláteras), portanto, não são deltaedros
 ). ).
Recorrido mínimo
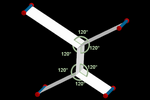
Os vetores que governam os movimentos das partículas podem estar
indefinidos. A cada passo, podemos experimentar com vários vetores e
escolher aquele que melhor se adapte ao nosso objetivo.
Neste exemplo, na simulação do conhecido experimento com película de
sabão, as partículas testam vários movimentos antes de decidir aqueles que
minimizam o comprimento total do perfil e, portanto, a área total da
superfície (neste caso, elas se dirigem aos pontos de Steiner [23]
dos quatro vértices). Os ângulos das lâminas são de 120º devido à
uniformidade na direção da distância euclidiana.
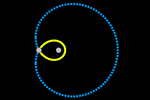
Órbita

Vamos ver em detalhes como é simples, graças ao seletor permanentemente animado, observar o movimento elíptico da Terra ao redor
do Sol sem recorrer à análise infinitesimal [20].
Nota: Esta construção foi feita a partir da
sugestão do meu colega de departamento, Julio Valbuena, que adaptou a
ideia exposta por Richard Feynman em seu famoso livro The Feynman Lectures on Physics
(volume I,
9-7, Planetary motions), ver Bibliografia.
Colocamos o ponto S (Sol) no centro das coordenadas e um ponto T (Terra)
com velocidade inicial o vetor v. Se d for a distância TS e k for uma
constante positiva, temos o vetor de força gravitacional:
g = k/d² VetorUnitário(S–T)
Agora, basta introduzir um seletor auxiliar para que, sempre que seja
atualizado, ele execute o script muito simples:
DefinirValor(v, v + 0.03 g)
DefinirValor(T, T + 0.03 v)
E já temos o movimento elíptico! (Observe que não usamos nenhuma equação
ou lugar geométrico.)
Caos

A construção anterior explica as órbitas quase perfeitamente elípticas dos
planetas ao redor do Sol. O "quase" é determinado pela presença de outros
corpos. Felizmente para os terráqueos, as órbitas dos outros planetas
estão suficientemente distantes para não perturbarem muito o nosso ano
solar. Aqui vemos o que aconteceria se não fosse assim. É uma
simplificação (dois corpos girando em torno de outro no mesmo plano) do
famoso "problema de três corpos"
 .
É impressionante observar como uma construção tão simples pode transformar
a ordem em caos [24]. .
É impressionante observar como uma construção tão simples pode transformar
a ordem em caos [24].
Bolhas (uso de
JavaScript)

Podemos usar vetores para modificar o movimento de um objeto com base na
distância em relação a outro, o que permite detectar colisões, por
exemplo. O problema é que se houver muitos objetos (n), o número de
eventos será elevado, pois cresce com o quadrado do número de objetos:
n(n–1)/2. Nestes casos, é melhor substituir os scripts do GeoGebra pelo
código JavaScript, que é mais rápido, como é feito nesta construção. Nela,
é mostrada uma colisão elástica, e podemos verificar a conservação
da energia cinética total em todos os momentos.
Tensegridades
A geometria elástica nos permite encontrar situações de equilíbrio entre
diferentes forças. Uma aplicação interessante são as estruturas de
tensegridade, compostas por barras e cabos sob tensão que as mantêm
unidas.
Tensegridade
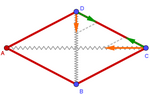
Se conectarmos diferentes vértices, obtemos o grafo de uma rede [25].
Mas se, além disso, as conexões forem feitas com barras e molas, podemos
fazer com que em posições específicas a tensão das molas se equilibre em
uma estrutura estável, chamada tensegridade
 . .
Aqui é mostrado um exemplo no plano. Graças ao fato de que o losango é um
paralelogramo, as forças em cada vértice se anulam, de modo que a
estrutura se mantém em equilíbrio estável em qualquer posição, desde que
as tensões horizontal e vertical sejam iguais.
|
Mais... |
Cálculo de tensões
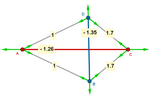
Agora, se partirmos de um quadrilátero qualquer, a
tensegridade só será alcançada para determinadas posições e tensões. Se
variarmos alguma dessas posições ou tensões, a estrutura buscará por si
mesma a nova posição de equilíbrio.
A chave está nos vértices: a soma vetorial das
forças envolvidas deve ser sempre nula.
|
Tensegridade de prisma triangular
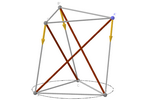
Vamos para o espaço. Uma das tensegridades mais simples
 começa com um prisma reto cujas bases são triângulos equiláteros.
Colocamos barras nas suas arestas laterais e cabos no resto. Agora, ao
tensionar os cabos, a tensegridade é alcançada quando uma das bases gira
exatamente 150º em relação à outra.
começa com um prisma reto cujas bases são triângulos equiláteros.
Colocamos barras nas suas arestas laterais e cabos no resto. Agora, ao
tensionar os cabos, a tensegridade é alcançada quando uma das bases gira
exatamente 150º em relação à outra.
Tensegridade icosaédrica tensionando cabos
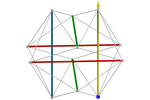
Um dos pioneiros das tensegridades, Buckminster Fuller, mostrou um
interesse especial
 por essa tensegridade. Consiste em uma estrutura formada por três pares de
barras paralelas, perpendiculares entre si, tensionadas por cabos. O
conjunto forma um icosaedro não convexo, conhecido como o icosaedro de Jessen
por essa tensegridade. Consiste em uma estrutura formada por três pares de
barras paralelas, perpendiculares entre si, tensionadas por cabos. O
conjunto forma um icosaedro não convexo, conhecido como o icosaedro de Jessen
 ,
cujos vértices não estão nas mesmas posições do icosaedro regular. ,
cujos vértices não estão nas mesmas posições do icosaedro regular.
Começamos com barras coladas duas a duas. Ao tensionar a estrutura, as
barras se afastam até que a direção da força resultante coincida com a da
barra. A proporção entre o comprimento de cada barra e cada cabo será,
então, exatamente
.png) (≈1.63).
Observamos que no icosaedro regular essa proporção é a do número áureo (≈1.62).
Podemos observar que o ângulo das faces do icosaedro de
Jessen é de 90º. (≈1.63).
Observamos que no icosaedro regular essa proporção é a do número áureo (≈1.62).
Podemos observar que o ângulo das faces do icosaedro de
Jessen é de 90º.
Tensegridade icosaédrica alongando barras
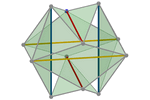
Podemos alcançar o mesmo resultado operando de forma inversa. Ou
seja, em vez de tensionar os cabos, tentamos alongar o máximo
possível as seis barras. Neste caso, partimos de um cuboctaedro.
Colocamos as barras e as esticamos ao máximo, mantendo o comprimento
original das arestas (os cabos) do cuboctaedro.
Conclusão
É verdade que a versão atual do GeoGebra é muito mais complexa do que sua
primeira versão de algumas décadas atrás. Temos tantos procedimentos e comandos
que é necessário um planejamento prévio para decidir, de acordo com o contexto,
quais deles realmente precisamos para alcançar nossos objetivos didáticos.
Nesta apresentação, verificamos, com numerosos exemplos, que o GeoGebra permite
enfrentar uma grande variedade de problemas com um mínimo de recursos. Enquanto
os comandos CAS tornam possível superar, em alguns casos, a dificuldade de
introduzir a álgebra no ensino secundário, as listas, vetores e scripts
adicionam facilidade para representar situações flexíveis, dinâmicas e
interativas. E, muitas vezes, tremendamente atraentes, tanto do ponto de vista
estético quanto no sentido de que convidam a explorar nossas próprias
construções (lembremos o efeito Ikea), o que favorece a aquisição da competência
matemática.
Agradecimentos
Embora nesta apresentação eu não tenha pretendido seguir os passos
das linhas expositivas realizadas por Tomás Recio em seu livro de
1998, Cálculo Simbólico y Geométrico
[30], devo reconhecer a enorme
influência que este livro, que recomendo vivamente, teve na minha
forma de compreender tanto a Matemática quanto o seu ensino. Além
disso, quero agradecer ao Tomás pelas suas sugestões e
esclarecimentos sobre alguns dos pontos aqui abordados.
Referências
[1] Álvarez, J.L. e Losada, R. (2011).
El proyecto
Gauss. Revista SUMA, número 68, pp. 17-25.
[2] Arranz, J.M., Losada, R., Mora, J.A. e Sada, M. (2008).
El cristo de la farola. Divulgamat, Real Sociedad Matemática
Española. Livro de GeoGebra:
G⁴D en Divulgamat
[3] Arranz, J.M., Losada, R., Mora, J.A. e Sada, M. (2010).
De luz y de color. Divulgamat, Real Sociedad Matemática Española.
Livro de GeoGebra:
G⁴D en Divulgamat
[4] Arranz, J.M., Losada, R., Mora, J.A., Recio, T. e Sada, M. (2009).
GeoGebra on the rocks. Dynamic Geometry Geometry Learn.
[5] Arranz, J.M., Losada, R., Mora, J.A., Recio, T.
e Sada, M. (2011).
Modeling the cube using GeoGebra. Model-Centered
Learning: Pathways to mathematical understanding using GeoGebra, pp.
119-131. Eds. L. Bu & R. Schoen (Eds.). Rotterdam: Sense Publishers.
[6] Calatayud, P. (2018).
El problema de la separación de elipses y elipsoides: una aplicación de la
eliminación de cuantificadores.
[7] Hohenwarter, M. (2006).
GeoGebra – didaktische Materialien und Anwendungen
für den Mathematikunterricht.
[8] Kovács, Z.
(2021).
Two almost-circles, and two real ones. Mathematics
in Computer Science 15, pp. 789–801.
[9] Losada, R. (2007).
La chica en
el espejo. Livro de GeoGebra.
[10] Losada, R. (2007).
GeoGebra: la eficiencia de la intución. La Gaceta de la Real Sociedad Matemática
Española, Vol. 10.1, pp. 223-239.
[11] Losada, R. (2009).
GeoGebra en
la Enseñanza de las Matemáticas. Ministério da Educação
e Formação Profissional. CD-ROM. ISBN: 978-84-369-4794-6.
[12] Losada, R., Recio, T. e Valcarce, J.L. (2009).
Sobre el descubrimiento
automático de diversas generalizaciones del Teorema de Steiner-Lehmus.
Boletín de la Sociedad Puig Adam, número 82, pp. 53-76. Universidade
Complutense de Madrid. Versão em inglês:
On the automatic discovery of Steiner-Lehmus generalizations.
[13] Losada, R. e Álvarez, J.L. (2010).
GeoGebra en
la Educación
Primaria. Ministério da Educação e Formação Profissional. CD-ROM.
ISBN: 978-84-369-4909-4.
[14] Losada, R. e Álvarez, J.L. (2011).
Proyecto Gauss.
Instituto de Tecnologías Educativas,
Ministério da Educação.
[15] Losada, R. (2011).
Dimensiones.
Livro de GeoGebra.
[16] Losada, R. (2011).
Modelos.
Livro de GeoGebra.
[17] Losada, R., Recio, T. e Valcarce, J.L. (2011).
Equal Bisectors at a Vertex of
a Triangle. Computational Science and Its Applications - ICCSA.
[18] Losada, R. e Recio, T. (2011).
Descubrimiento
automático en un problema centenario. La Gaceta de la Real Sociedad Matemática
Española, Vol. 14.4, pp. 693-702.
[19] Losada, R. (2014).
El
color dinámico de GeoGebra. La Gaceta de la Real Sociedad Matemática
Española. Vol. 17 (nº 3), 525–547. Livro de GeoGebra:
Color
dinámico.
[20] Losada, R. (2016).
La Tierra y
el Sol. Livro de GeoGebra. Versão em inglês: Earth and
Sun.
[21] Losada, R. (2017).
La
percepción del tamaño. Livro de GeoGebra.
[22] Losada, R. (2018).
Animaciones
automáticas. Livro de GeoGebra.
[23] Losada, R. (2018).
Autómatas.
Livro de GeoGebra.
[24] Losada, R. (2018).
Billares:
orden y caos. Livro de GeoGebra
[25] Losada, R. e Mora, J.A. (2021).
Redes y grafos. Las comunicaciones y la logística. Exposição
Matemáticas para un mundo mejor. Red DiMa, Dia Internacional da
Matemática. Livro de GeoGebra:
Redes y
Grafos.
[26] Losada, R. e Recio, T. (2021).
Mirando a los
cuadros a través de los ojos de Voronoi. Boletín de la
Sociedad Puig Adam, Vol. 112, pp. 32–53. Universidade Complutense de
Madrid. Livro de GeoGebra:
Voronoi
paintings.
[27] Losada, R. (2022).
Mapas de c@lor con GeoGebra. Revista SUMA. Número 102, pp. 43-57.
Livro de GeoGebra:
Mapas de c@lor
con GeoGebra.
[28] Losada, R. e Recio, T. (2023).
Inclinando la botella de Piaget con
GeoGebra Discovery. Boletín de la
Sociedad Puig Adam, Vol. 115, pp. 43-86. Universidade Complutense de
Madrid. Livro de GeoGebra:
Inclinando
la botella de Piaget con GeoGebra Discovery.
[29] Pérez, A., Sada, M. e Losada, R. (2021).
Fractales, la Geometría del Caos. Exposição Matemáticas para un
mundo mejor. Red DiMa, Dia Internacional da Matemática.
[30] Recio, T. (1998).
Cálculo Simbólico y Geométrico, Colección Educación Matemática en
Secundaria, Editora Síntesis, Madrid.
[31] Recio, T., Losada, R., Kovács, Z. e Ueno, C. (2021).
Discovering
Geometric Inequalities: The Concourse of GeoGebra Discovery, Dynamic
Coloring and Maple Tools. Mathematics 9 (20), 2548.
[32] Recio, T., Losada, R., Tabera, L.F. e Ueno, C. (2022).
Visualizing a Cubic Linkage through the Use of CAS and DGS.
Mathematics 2022, 10(15),
2550; https://doi.org/10.3390/math10152550. Livro de GeoGebra:
Mecanismos.
Versão em inglês:
Linkages.
Bibliografia
-
Arranz, J.M., Losada, R., Mora, J.A. e Sada, M. (2008).
Arcos con geometría dinámica. Matematicalia, Real Sociedad
Matemática Española, Vol. 4.1. Livro de GeoGebra:
Arte
y Geometría: Arcos
-
Arranz, J.M., Losada, R., Mora, J.A. e Sada, M. (2008).
Conjeturas a partir de los puntos medios. Divulgamat, Real Sociedad
Matemática Española. Livro de GeoGebra:
G⁴D en Divulgamat
-
Arranz, J.M., Losada, R., Mora, J.A. e Sada, M. (2008).
La percepción tridimensional. Divulgamat, Real Sociedad Matemática
Española. Livro de GeoGebra:
G⁴D en Divulgamat
-
Arranz, J.M., Losada, R., Mora, J.A. e Sada, M. (2008).
Geometría en rosetones góticos. Divulgamat, Real Sociedad
Matemática Española. Livro de GeoGebra:
G⁴D en Divulgamat
-
Arranz, J.M., Losada, R., Mora, J.A. e Sada, M. (2009).
Mosaicos con GeoGebra.
Coleção Lemniscata, número 7, pp. 57-87. Editora
Anaya. Livro de GeoGebra:
Arte y Geometría: Mosaicos
-
Arranz, J.M., Losada, R., Mora, J.A. e Sada, M. (2009).
Realities from GeoGebra. MSOR Connections Vol 9 No 2.
Versão espanhola:
Realidades de GeoGebra Revista SUMA. Número 67, pp. 7-20.
Reeditado por ocasião do
nº 100
em 2022. Livro de GeoGebra:
Realidades
de GeoGebra.
-
Botana, F., Kovács, Z., Recio, T. e Vélez, M.P. (2020).
Hacia
un autómata geómetra. La Gaceta de la Real Sociedad Matemática
Española, Vol. 23.2, pp. 343–371
-
Burkhardt, R.W. (2008).
A Practical Guide to Tensegrity Design.
-
Carrillo, A. e Recio, T. (2020).
De Curva a Curva,
con GeoGebra. Boletín de la
Sociedad Puig Adam, número 110.
-
Durán, A.J., Mora, J.A., Pereiro, D., Losada, R., Muñoz, J.L., Arranz, J.M.
(2021).
Matemáticas y belleza. Exposição Matemáticas para un
mundo mejor. Red DiMa, Dia Internacional da Matemática.
-
Feynman, R., Leighton, R.B. e Sands, M. (1963).
The Feynman Lectures on Physics, Mainly Mechanics, Radiations and Heat,
Volume I. Addison-Wesley.
-
Goicolea, J.M. (2021).
Cálculo de Cables. Universidade Politécnica de Madrid.
-
de Guzmán, M. (2002).
Tensegridad. De la escultura a la célula. Ars Medica. Revista de
Humanidades.
-
Losada, R. (2002).
All Lights y Lights Out: una investigación entre luces y sombras.
Revista SUMA. Número 40, pp. 25-41. Livro de GeoGebra:
Juegos de
iluminación (con soluciones). Versão em inglês:
Lights Out (games with solutions).
-
Losada, R. (2010).
Isometrías.
Livro de GeoGebra.
-
Losada, R. (2010).
Estadística
y Probabilidad. Livro de GeoGebra.
-
Losada, R. (2011).
Aritmética
y
cálculo mental. Livro de GeoGebra.
-
Losada, R. (2011).
Ecuaciones y
sistemas. Livro de GeoGebra.
-
Losada, R. (2011).
Funciones.
Livro de GeoGebra.
-
Losada, R. (2011).
Música
y
matemáticas. Divulgamat, Real Sociedad Matemática
Española. Livro de GeoGebra:
Música
y
Matemáticas
-
Losada, R. e Álvarez, J.L. (2011).
Los applets de funciones en el Proyecto Gauss. Revista UNO,
número 58, pp. 25-37. Editora Graó.
-
Losada, R. e
Álvarez, J.L. (2012).
Estadística
y probabilidad en el Proyecto Gauss. Revista UNO,
número 59, pp. 26-39. Editora Graó.
-
Losada, R. e
Álvarez, J.L. (2012).
La hoja de cálculo de GeoGebra. Revista UNO, número 61, pp.
55-66. Editora Graó.
-
Losada, R.
(2016).
Geogebra en el aula, un descubrimiento gradual. Revista UNO, número 71, pp. 13-19. Editora Graó.
-
Losada, R. (2021).
Cambio de
sistema de referencia. Livro de GeoGebra.
-
Losada, R. (2021).
Variable
compleja. Livro de GeoGebra.
-
Losada, R. (2021).
Julia y
Mandelbrot. Livro de GeoGebra.
-
Petrovic, M., Malesevic, B., Banjac, B. e Obradovic, R. (2014).
Geometry of some
taxicab curves.
-
Plaza, S. e
Gutiérrez, J.M. (2013).
Dinámica del método de Newton.
Universidade de La Rioja.
-
Ramellini, G.,
Losada, R. e Muñoz, J. (2021).
Juegos y Matemáticas. Exposição Matemáticas para un mundo mejor.
Red DiMa, Dia Internacional da Matemática. Livros de GeoGebra:
Juegos,
Rompecabezas,
Matemágicas.
-
San Segundo, F. (2010).
Effective
algorithms for the study of the degree of algebraic varieties in
offsetting processes.
|
![]()
![]()