MÓDULO 6

► 6. Problemas dirigidos

► 6.6 Puntos notables

Objetivos

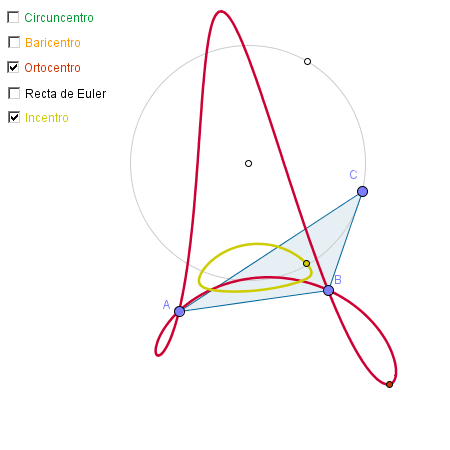
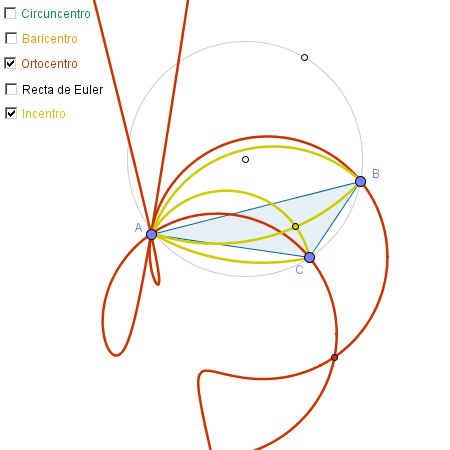
Se pretende ejemplificar el uso de GeoGebra como ayuda en la exploración, descubrimiento o comprobación de lugares geométricos. Hemos elegido algunos derivados de los puntos notables de un triángulo.

Herramientas

Usaremos las siguientes herramientas.

Punto	Intersección	Centro
Recta	Perpendicular	Bisectriz
Lugar	Polígono	Circunferencia
Circunferencia tres puntos	Casilla control

Construcción paso a paso

Antes de empezar, puede ser buena idea echar un vistazo al "Ejemplo de construcción" que se encuentra en esta página. Incluso podemos ayudarnos de la Barra de Navegación para realizar un rápido recorrido por los pasos.

Preparamos el escenario.

Preparación

No

No

Desactiva

Construimos la figura, de tal forma que uno de los vértices del triángulo descanse sobre una circunferencia.

Etapa 1

Herramienta Punto. Creamos los puntos A, B, D y E (renombramos el punto C como E).
Herramienta Circunferencia. Creamos la circunferencia de centro D que pasa por E.
Herramienta Punto. Colocamos un punto C en esa circunferencia.
Herramienta Polígono. Creamos el triángulo ABC. En las propiedades de los segmentos que se crean, activamos la opción de admitir intersecciones en las prolongaciones.

Construimos los puntos notables del triángulo.

Etapa 2

Herramienta Circunferencia tres puntos. Creamos la circunferencia que pasa por A, B y C.
Herramienta Centro. Indicamos el centro de la circunferencia anterior (circuncentro del triángulo). Ocultamos la circunferencia anterior.
Entrada: (A + B + C) / 3 (Esto crea el baricentro.)
Herramienta Recta. Trazamos la recta que pasa por el circuncentro y el baricentro (recta de Euler).
Herramienta Perpendicular. Trazamos dos alturas del triángulo.
Herramienta Intersección. Indicamos el punto de corte de las dos alturas (ortocentro). Ocultamos las perpendiculares anteriores.
Herramienta Bisectriz. Trazamos dos bisectrices interiores del triángulo.

Si para trazar una bisectriz hacemos clic sobre dos lados, aparecerá la bisectriz interior y la exterior. Si no se desea que también aparezca la exterior, hacer clic sobre los tres vértices (indicando así el ángulo a bisecar).

Herramienta Intersección. Indicamos el punto de corte de las dos bisectrices interiores (incentro). Ocultamos las bisectrices.

Mostramos los lugares geométricos correspondientes a los distintos puntos notables al recorrer el punto C la circunferencia. Para poder elegir qué se muestra en cada momento, añadimos unas casillas de control.

Etapa 3

Herramienta Lugar. Sucesivamente, hacemos clic sobre el circuncentro y C, el baricentro y C, el ortocentro y C, y finalmente, el incentro y C.
Herramienta Casilla control. Indicamos en cada caso el nombre de la casilla (Circuncentro, Baricentro, Ortocentro, Recta de Euler, Incentro) y los objetos a mostrar u ocultar (los puntos y lugares geométricos correspondientes).

Como siempre, completamos la construcción intentando mejorar el estilo y distribución de los objetos. La visualización temporal de la Cuadrícula nos puede ayudar a alinear las casillas de control.

Ejemplo de construcción

Puntos notables

Clic en esta imagen abre la construcción de GeoGebra

Propuesta de construcción

Realizar una construcción similar, algo menos general, con dos vértices del triángulo sobre la circunferencia. Ahora, para cada punto notable, se deberán crear dos lugares geométricos (según gire sobre la circunferencia un vértice u otro).

Comentarios

Dependiendo del nivel de conocimientos y experiencia de nuestros alumnos podemos usar esta construcción u otras similares para:

a) Comprobar que se cumple alguna relación (como la alineación del circuncentro, baricentro y ortocentro), o que se forma un lugar geométrico determinado para algunos puntos notables (como la circunferencia del baricentro).

b) Invitar a que descubran resultados sobre los puntos notables, sugiriendo preguntas clave.

c) Invitar a que construyan ellos mismos la figura.

d) Invitar a que descubran resultados sobre los lugares geométricos.

e) Invitar a que demuestren algunas propiedades, añadiendo si es preciso algunos elementos auxiliares a la construcción.

Investigación:

¿Para qué tipos de triángulos el incentro también descansará en la recta de Euler?
¿Si conocemos las posiciones del baricentro y del circuncentro de un triángulo (pero nada más), podemos determinar el ortocentro?
¿Se puede deducir el complejo lugar geométrico del ortocentro de los sencillos lugares del baricentro y circuncentro?
¿Qué sucede con los lugares cuando el triángulo es rectángulo?
¿En qué se diferencian los lugares de los triángulos acutángulos y obtusángulos?
¿Qué sucede cuando el circuncentro coincide con el centro del círculo donde descansa C?