ANEXOS
Manual
Imágenes
Inicio► Anexos
► Libertad restringida
|
Contenido |
Restringir la libertad de un punto a un área
La forma más sencilla de restringir un punto a una región plana es usando la
herramienta
Punto
en objeto, para lo cual debemos crear previamente la región.
Sin embargo, también hay dos formas excepcionales de definir un punto libre limitado a un círculo (o sector circular) centrado en el origen o al interior de un rectángulo cualquiera.
Observemos la siguiente construcción:
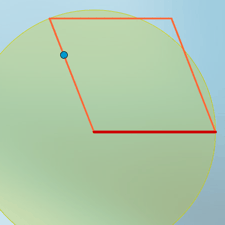
clic en esta imagen abre la
construcción de GeoGebra
Si el punto azul descansa sobre el segmento, ¿cómo es posible que dirija su movimiento?
El truco reside en que el punto azul no descansa sobre el segmento, sino que es este el que se construye a partir de aquel. El deslizador r varía entre 0 y 1.5, el deslizador α entre 0 y 360°. Un punto definido directamente como:
(r; α)
aún siendo dependiente, tendrá libertad de movimientos en los límites que permita r y α. Esto significa que el punto así definido estará restringido al sector circular centrado en el origen de coordenadas, de radio r y ángulo los límites de α.
En el modelo Módulo 4
Otros
modelos
Tangencial podemos ver un ejemplo de este uso.
En la siguiente construcción se muestra la otra excepción:
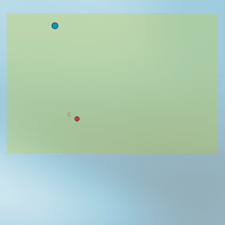
clic en esta imagen abre la
construcción de GeoGebra
Ahora hay dos parámetros a y b, con límites en [a1, a2] y [b1, b2], respectivamente. El punto azul está definido como:
(a+x(C), b+y(C))
donde C es otro punto cualquiera.
Un punto definido directamente de esta forma, aún siendo dependiente, tendrá libertad de movimientos en los límites que permita a y b. Esto significa que el punto así definido estará restringido al rectángulo con vértices opuestos en C + (a1,b1) y C + (a2,b2).
Coordenadas dinámicas y movimiento restringido
Gracias al comando CoordenadasDinámicas [O, x0, y0], podemos restringir las coordenadas de un punto por las expresiones x0 e y0. Estas dos coordenadas, o al menos una, deberían depender del punto inicial O. Esto permite crear puntos de movimiento restringido.
Llamemos A al punto resultante de aplicar este comando. Si lo movemos, el punto inicial O (que normalmente no debe ser visible) se mueve hasta la posición de A, a la vez que las coordenadas de A son calculadas de nuevo según las expresiones definidas por x0 e y0. Esto supone, en la práctica, la restricción de la libertad de arrastre de A a las condiciones impuestas en las expresiones con que se definen x0 e y0.
En los siguientes ejemplos partimos de un punto inicial O=(1,1) (que ocultamos):
- a = round(x(O))
b = round(y(O))
A = CoordenadasDinámicas[O, a, b]
Al intentar arrastrar A al punto (1.4, 2.7), el punto O ocupa inmediatamente esa posición, obligando a A a situarse en (1, 3).
- a = x(O)
b = Mínimo[y(O), sin(a)]
A = CoordenadasDinámicas[O, a, b]
La libertad de movimiento del punto A está restringida a posiciones por debajo de (o sobre) la gráfica de la función sin(x).
PuntoEn[y<sin(x)] crearía un punto similar.
- x0 = x(O)
y0 = y(O)
a = Si[x0>3, 3, Si[x0<-3, -3, Si[x0<1, round(x0), x0]]]
b = Si[x0<0, 0.5, Si[y0>2, 2, Si[y0<0, 0, y0]]]
A = CoordenadasDinámicas[O, a, b]
Basta activar el rastro del punto A para visualizar sus posibilidades de movimiento.
También podemos usar un tercer punto P=(2,2) para definir comportamientos restringidos por su posición:
- a = Si[Distancia[P, O] < 1, x(P), x(O)]
b = Si[Distancia[P, O] < 1, y(P), y(O)]
A = CoordenadasDinámicas[O, a, b]
El punto P se convierte en un atractor de A, cuando este se aproxima a él.
