ANEXOS
► Anexos
► Transformaciones
|
Contenido |
Transformaciones
Además de las isometrías, la homotecia y la inversión, que se detallan a continuación, podemos realizar cualquier transformación lineal o afín con ayuda del comando AplicaMatriz.
 Traslación
Traslación
La
imagen de cada punto P en una traslación
![]() es:
es:
P' = P + v
donde v es el vector de traslación.
 Rotación
Rotación
La
imagen de cada punto P en una rotación
![]() es (isometrias.ggb):
es (isometrias.ggb):
P' = O + M (P - O)
donde O es el centro de rotación, α es el ángulo de rotación y M es la matriz de rotación:
M = {{cos(α), -sin(α)}, {sin(α), cos(α)}}
![]() Casos
particulares:
Casos
particulares:
- Una rotación de 180° equivale a una simetría central, es decir, a reflejar sobre el centro de rotación: Refleja[A, 180°, O] equivale a Refleja[A, O]
- Si O es el origen de coordenadas, la imagen de cada punto es P' = M P
 Simetría axial
Simetría axial
La
imagen de cada punto P en una simetría axial
![]() es (isometrias.ggb):
es (isometrias.ggb):
P' = O + M (P - O)
donde O es un punto cualquiera de la recta y, si α es el ángulo que forma la recta r con la horizontal, M es la matriz de simetría axial:
M = {{cos(2α), sin(2α)}, {sin(2α), -cos(2α)}}
![]() Casos
particulares:
Casos
particulares:
- La imagen del eje de simetría es él mismo: Refleja[r, r] = r
- Reflejar dos veces sobre el mismo eje crea una copia del objeto: Refleja[Refleja[a, r], r] = a
- Refleja[P, EjeX] = (x(P), -y(P))
- Refleja[P, EjeY] = (-x(P), y(P))
- Si r: y = x entonces Refleja[P, r] = (y(P), x(P))
- Si r: y = -x entonces Refleja[P, r] = -(y(P), x(P))
 Simetría central
Simetría central
Si
O es el centro de simetría, la
imagen de cada punto P en una simetría central
![]() es:
es:
P' = O + (-1) (P - O) = 2O - P
![]() Casos
particulares:
Casos
particulares:
- El centro se refleja en sí mismo: Refleja[O, O] = O
- Si elegimos el origen de coordenadas como centro, la imagen de cualquier punto será su opuesto: Refleja[(0,0), P] = -P
 Homotecia
Homotecia
La
imagen de cada punto P en una homotecia
![]() de centro O es:
de centro O es:
P' = O + M (P - O)
donde M es la matriz de escala con factor k:
M = {{k, 0}, {0, k}}
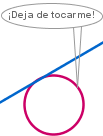
 Inversión
Inversión
Si
O es el centro de la circunferencia de radio r, la imagen de cada punto P
en una inversión
![]() es la
intersección de la semirrecta OP con la circunferencia de centro O y radio
r²/OP (inversion.ggb).
es la
intersección de la semirrecta OP con la circunferencia de centro O y radio
r²/OP (inversion.ggb).
![]() Casos
particulares:
Casos
particulares:
- Si A está en c, entonces Refleja[A, c] = A
- La inversión de la circunferencia en ella misma es de nuevo ella misma: Refleja[c, c] = c
- Refleja[Refleja[A, c], c] = A
- Reflejar dos veces sobre la misma circunferencia crea una copia del objeto: Refleja[Refleja[a, c], c] = a