ANEXOS
► Anexos
► Parámetro punto
|
Contenido |
Punto inicial y parámetro sobre recorrido
Si creamos un deslizador t, entre 0 y 1, y el punto P = Punto [a, t] que se sitúa en el recorrido del objeto a según sea el valor de t, la posición exacta de P depende del tipo de objeto que sea a.
Por otra parte, si usamos el comando Punto[a] para crear un punto en el recorrido del objeto a, su valor inicial P0 no tiene por qué coincidir con la posición de P correspondiente al valor 0 del parámetro t.
Posición del punto inicial del comando Punto[a]
La primera posición asignada al crear el punto P0 = Punto[a] es la que ofrece el comando:
P0 = PuntoMásPróximo[a, (0,0)]
- Si el objeto es geométrico (incluyendo lugares geométricos, curvas parametrizadas, funciones implícitas y recorridos combinados), ese punto es el punto de a más próximo al origen de coordenadas.
- Si el objeto es una función f(x), la primera posición asignada será (0, f(0)), pues esta es el punto más próximo "en vertical" al origen de coordenadas. Así sucede, por ejemplo, para cualquier polinomio.
Si la función no está definida en 0 (ni siquiera toma un valor infinito, como 1/x o log(x)), y dependiendo del modo en que se haya definido, o bien se le asigna el valor de la abscisa más cercana, o bien se considera indefinido. En este último caso puede resultar útil reasignarle coordenadas al punto:
f(x) = sqrt(x-2) P0 = Punto[f]
El valor de P0 será indefinido. Así que puede convenir reasignarle una posición:
Coordenadas[P0, 4, 0]
Este comando no redefine P0, sino que lo reedita, de tal forma que no deja de pertenecer a la gráfica de f. Esto es, el punto P0 pasa a tomar las coordenadas (4, f(4)):
Coordenadas[P0, 4, 0] equivale a Coordenadas[P0, 4, f(4)] si P0 es un punto del recorrido de la gráfica de f.
- Por último, si se usa P0 = Punto[L], donde L es una lista de recorridos, la primera posición P0 asignada en el recorrido combinado de los objetos de L será el punto más próximo al origen de las distintas posiciones encontradas según los criterios mencionados para objetos geométricos y funciones.
Posición del punto respecto a su parámetro t en el recorrido: comando Punto[a, t]
- a = Segmento [A, B]
P = A + λ (B - A), donde λ es la razón simple de A, B y P, con λ = t.
Casos particulares:
Si t = 0 entonces P = A.
Si t = 0.5 entonces P = PuntoMedio[A,B].
Si t = 1 entonces P = B.
Si a es un intervalo de extremos x1 y x2 (no importa si es abierto o cerrado), entonces P = Punto [a, t] recorrerá el segmento A, B, donde A=(x1, 0) y B= (x2, 0).
- a = Vector [A, B]
P = A + λ (B - A), donde λ es la razón simple de A, B y P, con λ = t.
Casos particulares:
Si t = 0 entonces P = A.
Si t = 0.5 entonces P = PuntoMedio[A,B].
Si t = 1 entonces P = B.
P = A + λ (B - A), con λ = t/(1-t)
Casos particulares:
Si t = 0 entonces P = A.
Si t = 0.5 entonces P = B.
Si t = 1 entonces P es un punto del infinito.
- a = Recta [A, B]
P = A + λ (B - A), con λ = (2t-1)(1+abs(2t-1))/(4t (1-t))
Casos particulares:
Si t = 0 entonces P es un punto del infinito.
Si t = 0.25 entonces P = 2A-B (simétrico de B respecto a A).
Si t = 0.5 entonces P = A.
Si t = 0.75 entonces P = B.
Si t = 1 entonces P es un punto del infinito.
|
- a = Polígono [L] (donde L es la lista ordenada de vértices).
P = Suma[Secuencia[Si[(t Longitud[L] - (j-1)<0) ∨ (t Longitud[L] - (j-1)≥1) ∧ (j<Longitud[L]), (0, 0), Elemento[Anexa[L, Elemento[L, 1]], j] + (t Longitud[L] - (j-1)) (Elemento[Anexa[L, Elemento[L, 1]], j+1] - Elemento[Anexa[L, Elemento[L, 1]], j])], j, 1, Longitud[L]]]
Casos particulares:
Si t = 0 entonces P = Elemento[L, 1] (el primer vértice del polígono).
Si t = (j-1)/Longitud[L] entonces P = Elemento[L, j] (el j-ésimo vértice del polígono).
Si t = 1 entonces P = Elemento[L, 1] (el primer vértice del polígono).
Según t recorre [0,1], el punto P recorre la circunferencia en sentido antihorario:
P = Rota[O - (abs(A-O), 0), 2pi t, O]
Casos particulares:
Si t=0 o t=1, entonces P = O - (abs(A-O), 0).
Es decir, el punto inicial del recorrido es el punto de la circunferencia de menor abscisa.
Según t recorre [0,1], el punto P recorre la circunferencia en sentido antihorario:
P = Rota[B, pi t, (A+B)/2]
Casos particulares:
Si t=0 entonces P = B.
Si t=0.5 entonces P es el punto medio de la semicircunferencia.
Si t=1 entonces P = A.
Es decir, el punto inicial siempre es B y el final siempre es A (ya que los arcos siempre se recorren en sentido antihorario).
- a = Arco [O, A, B]
Según t recorre [0,1], el punto P recorre el arco en sentido antihorario:
P = Rota[A, Angulo[A, O, B] t, O]
Casos particulares:
Si t=0 entonces P = A.
Si t=0.5 entonces P es el punto medio del arco.
Si t=1 entonces P = B.
Es decir, el punto inicial siempre es A y el final siempre es B (ya que los arcos siempre se recorren en sentido antihorario).
Según t recorre [0,1], el punto P recorre la elipse en sentido antihorario.
Casos particulares:
Si t=0 o t=1, entonces
P = Si[(x(P2)<x(P1)) ∨ x(P2)≟x(P1) ∧ (y(P2)<y(P1)), P2, P1]
donde
P1 = (F1+F2)/2 + (abs(F1-A) + abs(F2-A))/2 (F1-F2)/abs(F1-F2)
P2 = (F1+F2)/2 - (abs(F1-A) + abs(F2-A))/2 (F1-F2)/abs(F1-F2)
Es decir, el punto inicial del recorrido es el vértice del eje principal de la elipse de menor abscisa, y en caso de que el eje principal sea una vertical, de menor ordenada.
Para t=0.25, 0.5 y 0.75, el punto P se posiciona en los otros 3 vértices de la elipse.
- a = Parábola [F, r]
Los puntos inicial (t=0) y final (t=1) se encuentran indefinidos.
Casos particulares:
Si t=0.5 entonces P se posiciona en el vértice de la parábola.
Los puntos inicial (t=0) y final (t=1), así como el punto medio (t=0.5), se encuentran indefinidos.
Casos particulares:
Para t=0.25 y t=0.75, el punto P se posiciona en los vértices de la hipérbola.
- Si a es un lugar geométrico, entonces P = Punto[a, t] recorrerá el lugar geométrico comenzando (t=0) y finalizando (t=1) en la posición del punto generador.
|
- Si f(x) es una función, entonces P = Punto[f, t] equivale a:
P = (x(Esquina[1])+t x(Esquina[2]-Esquina[1]), f(x(Esquina[1])+t x(Esquina[2]-Esquina[1])))
Casos particulares:
Si t=0, P toma el valor de la abscisa de la Esquina[1] de la vista gráfica (tope izquierdo).
Si t=0.5, P toma el valor de la abscisa del centro de la vista gráfica.
Si t=1, P toma el valor de la abscisa de la Esquina[2] de la vista gráfica (tope derecho).
- Si c(t) es una curva paramétrica en [t1, t2], entonces P = Punto[c, t] equivale a:
P = c((t2-t1)t)
Es decir, el valor del parámetro t coincide con el del parámetro t una vez normalizado (una vez dividido por el ancho del intervalo de su recorrido).
|
Paralelas y perpendiculares
La definición de una recta afecta a paralelas y perpendiculares. En los siguientes ejemplos se detalla la causa.
|
clic en esta imagen |
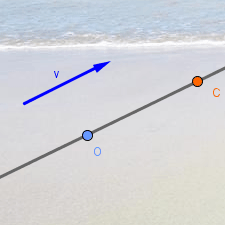
Una recta definida por un punto O y un vector
v tiene por ecuación vectorial:
X = O + λ v
Al colocar un punto C en esa recta, GeoGebra le asigna un valor λC del parámetro λ.
Si variamos el módulo de v, el parámetro λC se mantiene constante, por lo que varía la posición absoluta de C. Es decir, GeoGebra toma el módulo del vector director v como “vector base” de la recta. |
|
clic en esta imagen |
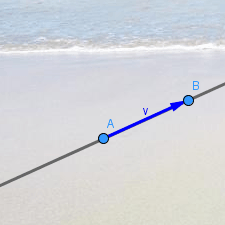
Una recta definida por dos puntos A y B
equivale a estar definida por el punto A y el vector v = AB. Ecuación
vectorial:
X = A + λ v
Al colocar un punto C en esa recta, GeoGebra le asigna un valor λC del parámetro λ.
Si variamos la posición de B, el parámetro λC se mantiene constante, por lo que varía la posición de C. |
|
clic en esta imagen |
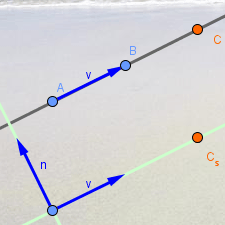
GeoGebra usa el vector director v de la recta
para establecer el vector director de cualquier recta paralela (v) y el
vector director de cualquier recta perpendicular (n, normal a v).
Así que al variar el módulo de v (por ejemplo, arrastrando B) todos los puntos de las tres rectas (r, s y t) se desplazan, ya que la posición de todos esos puntos depende de A y B. |