TIPOS DE OBJETOS
► Tipos de objetos
► Recorridos
Introducción
Los recorridos son todas los objetos cuya representación gráfica es una línea (o
un punto). En un recorrido que sea una línea, siempre podemos colocar un punto
que la recorra, bien con la herramienta
![]() Punto,
bien con el comando Punto.
Punto,
bien con el comando Punto.
Para liberar un punto A de ese recorrido basta redefinirlo con dos coordenadas cualesquiera, por ejemplo, A = (0, 0).
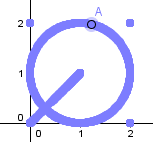
Una lista con diversos objetos con recorrido configura a su vez un solo recorrido. Por ejemplo, podemos colocar un punto sobre un recorrido formado por tres puntos, un segmento y una circunferencia:
- Punto[{(0,2), (2,0),(2,2), Segmento[(0,0),(1,1)], Circunferencia[(1,1),1]}]
Este punto está restringido a moverse por esos recorridos (hemos activado el rastro del punto para comprobarlo mejor).
Algunas herramientas y comandos que no figuran en esta página crean algunas líneas que favorecen la interpretación visual de un resultado. Por ejemplo, la herramienta
Pendiente o el comando IntegralEntre. Pero estos trazos no son recorridos que podamos reutilizar como elementos geométricos, no son objetos, solo son representaciones gráficas.
Punto inicial y parámetro sobre recorrido.
Los puntos sujetos a un recorrido se pueden reeditar, sin redefinirlos, usando
Mayús doble clic
en la Vista Algebraica. Así, podemos cambiar su posición en el recorrido sin que deje de pertenecer a él. Videoclip
Recorridos predefinidos: Ejes de coordenadas
Podemos hacer referencia a los ejes cartesianos de abscisas y ordenadas con los nombres respectivos de EjeX e EjeY.
- Perpendicular[(1, 1), EjeX] traza una recta perpendicular al eje de abscisas por el punto (1, 1).
Puntos
Existe una variedad de herramientas de
puntos y comandos de puntos, que
nos permiten crear nuevos puntos
![]() .
.
También podemos crear puntos directamente en el Campo de Entrada, introduciendo sus coordenadas cartesianas (separadas por coma) o polares (separadas por punto y coma). En este último caso, si no introducimos el símbolo ° de grados, se entenderá que el ángulo se encuentra expresado en radianes.
Por defecto, las mayúsculas (A, B...) rotulan puntos y las minúsculas (u, v...) vectores.
- (1, 0) crea el punto (1, 0) y le asigna el primer nombre disponible, con inicial mayúscula (A, B...).
- P: (1, 0) crea el punto (1, 0) y le asigna el nombre P.
- P = (1, 0) crea el punto (1, 0) y le asigna el nombre P.
- P = (1 ; 45°) crea el punto P de esas coordenadas polares.
También podemos realizar operaciones con puntos, pues estos son interpretados como vectores de posición.
- Si A = (1, 2) y B = (3, 4), entonces C = (A + B) / 2 devolverá el punto de coordenadas (2, 3), punto medio de los puntos A y B.
- Si A = (1, 2) entonces C = A + 1 devolverá el punto (2, 3), resultado de sumar 1 a las dos coordenadas de A.
Un punto también puede ser considerado el afijo de un número complejo. Así, el punto (a, b) admite la expresión compleja a + b i. En tal caso, la suma anterior devolverá un resultado diferente:
- Si A = 1 + 2i entonces C = A + 1 devolverá el número complejo 2 + 2i, resultado de sumar 1 únicamente a la parte real de A.
Para referenciar las coordenadas de un punto:
x(A) y(A)
abscisa de un punto x((2, 3)) = 2 y((2, 3)) = 3
Rectas
Existe una variedad de herramientas de
rectas y comandos de rectas, que
nos permiten crear nuevas rectas
![]() .
.
La ecuación paramétrica de la recta r que pasa por A y B es r: X = A + λ (B-A)
Una recta se puede ingresar directamente en el Campo de Entrada como una ecuación lineal en x e y o en forma paramétrica. En ambos casos, se pueden emplear variables previamente definidas (números, puntos, vectores).
Podemos anotar el nombre de la recta encabezando la entrada, seguido de los dos puntos.
- Podemos definir una recta r ingresando la ecuación r: 3x + 4y = 2 como ecuación lineal.
- Podemos ingresar la recta r en formato paramétrico como r: X = (-5, 5) + t (4, -3)
- Deben definirse los parámetros m = 2 y b = -1 antes de ingresar la ecuación r: y = m x + b para obtener la ecuación explícita de una recta r.
Las rectas pueden usarse como funciones: a: y = 2x a(3)
Semirrectas
Existe una herramienta de
semirrecta y un par de
comandos de semirrectas, que nos permite crear nuevas semirrectas
![]() .
.
Una semirrecta tiene la misma forma paramétrica X = A + λ (B-A) que una recta, pero con el parámetro λ restringido a los números no negativos. Ver el apartado Rectas.
Al formar parte de rectas, por tanto con la misma ecuación, no hay modo de ingresar directamente ecuaciones de semirrectas en el Campo de Entrada.
Punto inicial y parámetro sobre recorrido.
El uso de semirrectas en vez de rectas puede resultar especialmente conveniente para determinar un punto de corte. Por ejemplo, una recta que pase por el centro de una circunferencia la cortará en dos puntos, mientras que una semirrecta determinará unívocamente un punto de intersección.
Segmentos
Existe una variedad de
herramientas de segmentos y
comandos de segmentos, que nos permiten crear nuevos segmentos
![]() .
.
Un segmento tiene la misma forma paramétrica X = A + λ (B-A) que una recta, pero con el parámetro λ restringido al intervalo [0,1]. Ver el apartado Rectas.
Al formar parte de rectas, por tanto con la misma ecuación, no hay modo de ingresar directamente ecuaciones de segmentos en el Campo de Entrada.
Vectores
Existe una variedad de
herramientas de vectores y comandos de
vectores, que nos permiten crear nuevos vectores
![]() .
.
También podemos crear vectores libres (representados con extremo inicial en el origen de coordenadas) directamente en el Campo de Entrada, nominándolos con una minúscula (para distinguirlos de los puntos) e introduciendo sus componentes cartesianas (separadas por coma) o polares (separadas por punto y coma). En este último caso, si no introducimos el símbolo ° de grados, se entenderá que el ángulo se encuentra expresado en radianes.
Por defecto, las mayúsculas (A, B...) rotulan puntos y las minúsculas (u, v...) vectores.
- (1, 0) crea el punto (1, 0) y le asigna el primer nombre disponible, con inicial mayúscula (A, B...).
- v: (1, 0) crea el vector libre (1, 0) y le asigna el nombre v.
- v = (1, 0) crea el vector libre (1, 0) y le asigna el nombre v.
- v = (1 ; 45°) crea el vector libre que tiene como extremo final el punto de esas coordenadas polares.
Para referenciar las componentes de un vector v:
x(v) y(v)
primera componente del vector v segunda componente del vector v
x((2, 3)) = 2 y((2, 3)) = 3
Circunferencias
Existe una variedad de
herramientas de
circunferencias y comandos de
circunferencias, que nos permiten crear nuevas circunferencias
![]() .
.
También podemos crear circunferencias directamente en el Campo de Entrada, Una circunferencia se ingresa como una ecuación cuadrática (particular) en x e y. Se pueden emplear variables previamente definidas (números, puntos, vectores...). El nombre de la circunferencia puede ser anotado encabezando la entrada, seguido de dos puntos.
Además de recorrido, todas las circunferencias tienen una región asociada (el círculo).
- Circunferencia c1: x² + y² = 25
- Circunferencia c2: (x – 5)² + (y + 2)² = 25
Cónicas
Existe una variedad de herramientas de
cónicas y comandos de
cónicas, que nos permiten crear nuevas cónicas
![]() .
.
También podemos crear cónicas directamente en el Campo de Entrada. Una cónica se ingresa como una ecuación cuadrática (general) en x e y. Se pueden emplear variables previamente definidas (números, puntos, vectores...). El nombre de la cónica puede ser anotado encabezando la entrada, seguido de dos puntos.
Además de recorrido, todas las cónicas tienen una región asociada.
- Elipse e: 9 x² + 16 y² = 144
- Hipérbola h: 9 x² – 16 y² = 144
- Parábola p: y² = 4 x
- Dados dos parámetros a = 4 y b = 3, podemos ingresar una elipse como e: b² x² + a² y² = a² b²
Arcos (o sectores)
Existe una variedad de
herramientas de arcos y sectores y
comandos de arcos y sectores, que nos permiten crear nuevos arcos
![]() y sectores
y sectores
![]() (también de elipses, en el caso de usar comandos).
(también de elipses, en el caso de usar comandos).
Al formar parte de circunferencias, por tanto con la misma ecuación, no hay modo de ingresar directamente en el Campo de Entrada alguna ecuación que produzca arcos o sectores.
Tanto los arcos como sectores tienen, además de recorrido, una región asociada. La diferencia reside en que el valor que recoge el arco es el valor de su longitud, mientras que el sector recoge el valor de su área.
El uso de arcos y semicircunferencias
en vez de circunferencias puede resultar especialmente conveniente para determinar un punto de corte. Por ejemplo, una recta que pase por el centro de una circunferencia la cortará en dos puntos, mientras que solo cortará a un arco menor de 180° en un punto.
Polígonos
Existe una variedad de herramientas de
polígonos y comandos de
polígonos, que nos permiten crear nuevos polígonos
![]() .
.
Los polígonos quedan determinados por las rectas sobre las que descansan sus lados, cada una con su ecuación, por lo que no hay modo de ingresar directamente en el Campo de Entrada alguna ecuación que produzca polígonos.
Un polígono se compone de varios objetos, que se crearán al mismo tiempo que él (junto con los vértices, si no existen previamente):
- Los lados (segmentos).
- El área del polígono, que es una región asociada (cuyo valor aparece en la Vista Algebraica).
El polígono puede ser no convexo. Incluso puede ser cruzado (estrellado).
Punto inicial y parámetro sobre recorrido.
Si los vértices son libres, los lados se pueden arrastrar.
Poligonales
Existe una herramienta de
poligonal y un par de
comandos de
poligonales, que nos permiten crear nuevas poligonales
![]() .
.
Una poligonal está formada por segmentos concatenados por lo que no hay modo de ingresar directamente en el Campo de Entrada alguna ecuación que produzca poligonales.
Lugares Geométricos
Existe una herramienta de lugar
geométrico y un comando
de lugar geométrico, que nos permiten crear nuevos lugares geométricos
![]() .
.
En GeoGebra, un lugar geométrico es el recorrido que realiza un punto B que depende de un punto A que está sobre un recorrido previo. A medida que A recorre su objeto de recorrido, el punto B recorrerá una cierta trayectoria que constituye el nuevo lugar geométrico. Ya que se trata del resultado de un proceso constructivo punto a punto, no hay modo de ingresar directamente en el Campo de Entrada alguna ecuación que produzca un lugar geométrico de esta naturaleza.
Ecuaciones y = f(x): funciones explícitas
Existe una variedad de comandos de
polinomios y comandos de funciones, que nos permiten crear nuevas
funciones
![]() .
.
También podemos crear funciones explícitas directamente en el Campo de Entrada. Una función se ingresa como una ecuación en x. Se pueden emplear variables previamente definidas (números, puntos, vectores...). El nombre de la función puede ser anotado encabezando la entrada, seguido de dos puntos.
- Función f: f(x) = 3 x³ – x²
- Función g: g(x) = tan(f(x))
- Función sin nombre (se asignará automáticamente): sin(3x) + tan(x)
|
Todas las funciones predefinidas (como seno, logaritmo, etc.) se describen en la sección dedicada a operaciones.
Si A es un punto, se admite la expresión
f(A) como equivalente a f(x(A)).
Por ejemplo, el punto de la gráfica de la función f en la misma vertical que
el punto A es el punto (x(A), f(A)).
|
Existen comandos para obtener la Integral y Derivada de una función.
También se puede emplear f’(x) o f’’(x),… para las derivadas de una función f(x) previamente definida:
- Tras definir la función f como f(x) = 3 x³ – x² se puede ingresar g(x) = cos(f’(x + 2))
Además, las funciones pueden ser trasladadas
por un vector y una función puede, en principio, ser arrastrada con la
herramienta fundamental
![]() Elige y mueve.
Elige y mueve.
| Otras herramientas de transformación y comandos de transformación pueden aplicarse a funciones. Dependiendo de la transformación elegida el objeto resultante será una nueva función (traslación, homotecia) o una curva paramétrica (reflexión, rotación...). |
- Refleja[x², y=x] devuelve una parábola con eje el EjeX.
Para limitar una función a un intervalo [x1, x2], debe emplearse el comando Función[f(x), x1, x2].
Puede usarse el comando lógico Si para crear una función definida a trozos:
Si [condición, f(x), g(x)]
- Si [x < 1, x + 3, x - 1]
- Si [x < 1, Función[x + 4, -10, 1], x - 1]
Pueden usarse derivadas e integrales de tales funciones, o intersecarlas, como funciones “normales”.
Ecuaciones x = f(t), y = g(t): curvas paramétricas
El comando Curva permite crear
una curva de ecuación paramétrica
![]() e(t) = (f(t), g(t)), con t en un intervalo [t1,
t2]. No se puede ingresar directamente la ecuación paramétrica de
una curva en el Campo
de Entrada.
e(t) = (f(t), g(t)), con t en un intervalo [t1,
t2]. No se puede ingresar directamente la ecuación paramétrica de
una curva en el Campo
de Entrada.
Las curvas paramétricas pueden usarse con otras funciones o en expresiones aritméticas. Así, dada la curva e, la entrada e(3) devuelve el punto correspondiente a la posición t = 3. Los valores t1 y t2 pueden ser variables, por ejemplo deslizadores, creándose así rangos dinámicos.
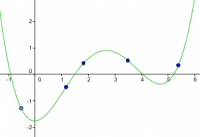
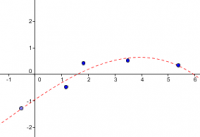
Como no siempre es posible crear curvas paramétricas que pasen por ciertos puntos dados, puede resultar mejor en esos casos usar el comando Polinomio o algún comando de curva de regresión, como AjustePolinómico o AjusteExp. Por ejemplo, si colocamos cinco puntos A, B, C, D y E en la vista gráfica, podemos después introducir los siguientes comandos:
Polinomio[{A,B,C,D,E}]
AjustePolinómico[{A,B,C,D,E}, 3]
Ecuaciones f(x, y) = 0: funciones implícitas
El comando CurvaImplícita
permite crear una curva de ecuación implícita
![]() f(x,y) = 0, donde f(x,y) es un
polinomio en x e y.
f(x,y) = 0, donde f(x,y) es un
polinomio en x e y.
Podemos ingresar directamente la ecuación en el Campo de Entrada.
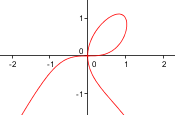
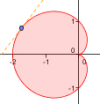
x⁴ - 2x y + y³ = 0 |
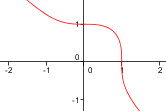
x³ + y³ = 1 |
Las curvas implícitas admiten transformaciones isométricas, homotecias e inversiones.
Intervalos
Un intervalo es el conjunto de números comprendido entre dos números dados (extremos). Podemos introducir intervalos directamente en el Campo de Entrada, tanto con la variable x como con la variable y.
- s: 2 < x < 3 corresponde al intervalo abierto (2, 3), es decir, excluidos el 2 y el 3.
- s: x > 2 && x < 3 es otra forma de introducir el mismo intervalo anterior.
- s: 2 < y < 3 es un intervalo equivalente, con representación gráfica sobre el EjeY.
También podemos ingresar intervalos cerrados (2 ≤ x ≤ 3) y semicerrados (2 ≤ x < 3 o 2 < x ≤ 3).
Para determinar si un número x0 pertenece a un intervalo s, escribimos s(x0) en el Campo de Entrada. El resultado será una constante lógica (true o false).
Además de recorrido, todos los intervalos tienen una región asociada, una franja correspondiente a los puntos (x, y) tales que x pertenece al intervalo (franja vertical, si el intervalo usa la variable x), o bien tales que y pertenece al intervalo (franja horizontal, si el intervalo usa la variable y). Las regiones determinadas por inecuaciones constituyen una generalización de estas franjas.
Podemos colocar un punto en un intervalo con la herramienta
Punto o con el comando Punto.
- Punto[2 < x] coloca un punto en la semirrecta correspondiente.
- PuntoEn[2 < x] coloca un punto en el semiplano correspondiente.